
- •Характеристики систем автоматического управления и их звеньев.
- •Временные характеристики систем автоматического управления и их звеньев.
- •Характеристики интегрирующего звена.
- •Временные характеристики.
- •Частотные характеристики интегрирующего звена.
- •Апериодическое звено.
- •Правило построения логарифмической амплитудно-частотной характеристики апериодического звена.
- •Колебательное звено.
- •Характеристики колебательного звена.
- •Временные характеристики.
- •Частотные характеристики колебательного звена.
- •Логарифмическая амплитудно-частотная и фазо-частотная характеристики колебательного звена.
- •Дифференцирующее звено первого порядка.
- •Характеристики дифференцирующего звена первого порядка.
- •Временные характеристики.
- •Частотные характеристики.
- •Дифференцирующее звено второго порядка. Математические модели
- •Временные характеристики:
- •Частотные характеристики:
- •Логарифмические частотные
- •Правило построения асимптотических амплитудно-частотных характеристик разомкнутых систем автоматического управления.
- •Об устойчивости.
- •О переходном процессе.
- •О точности системы.
- •Точность систем автоматического управления при гармоническом входном воздействии.
- •Основные виды корректирующих устройств систем автоматического управления.
- •Последовательные корректирующие устройства.
- •Введение производной от ошибки.
- •Увеличение общего коэффициента усиления разомкнутой системы.
- •Введение интеграла от сигнала ошибки системы.
- •Изодромное корректирующее устройство.
- •Параллельные корректирующие устройства.
- •Положительная жесткая обратная связь.
- •Отрицательная жесткая обратная связь.
- •Инерционная жесткая обратная связь.
- •Гибкая обратная связь.
- •Инерционная гибкая обратная связь.
- •Корректирующие устройства по внешнему воздействию. Инвариантность.
- •Корректирующее устройство по задающему воздействию.
- •Корректирующее устройство по возмущению.
- •Краткое сравнение способов коррекции систем автоматического управления при помощи последовательных и параллельных корректирующих устройств.
- •Принцип дуальности управляемости и наблюдаемости.
- •В соответствии с последними уравнениями структурная схема системы имеет вид (сравнить с исходной структурной схемой).
- •Пусть заданна передаточная функция замкнутой системы
- •Или в векторно-матричной форме записи
- •Или в векторно-матричной форме записи
- •Уравнения (7)-(8), а, следовательно, и (9),(10), имеют каноническую форму записи, каноническая форма управляемости.
- •Пример. Задана желаемая передаточная функция разомкнутой системы ,
- •Решение. Желаемая передаточная функция замкнутой системы
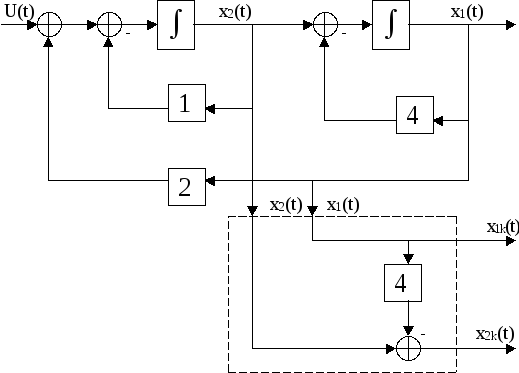
- •Пример. Структурная схема объекта управления имеет вид, показанный на рисунке
- •Решение. Введем обозначения
В соответствии с последними уравнениями структурная схема системы имеет вид (сравнить с исходной структурной схемой).
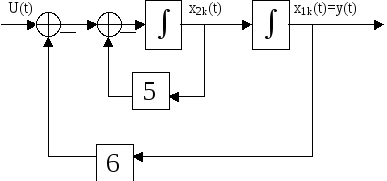
![]()

Пример. Система автоматического управления описывается уравнениями
![]() ,
,
![]() ,
,
![]() .
.
П![]() ривести
данную математическую модель системы
к канонической форме записи.
ривести
данную математическую модель системы
к канонической форме записи.
Решение. Для данной системы имеем:
 ,
,
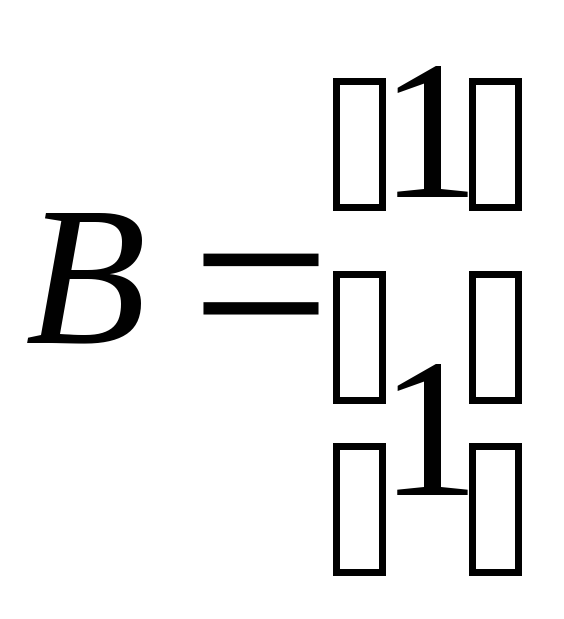 ,
,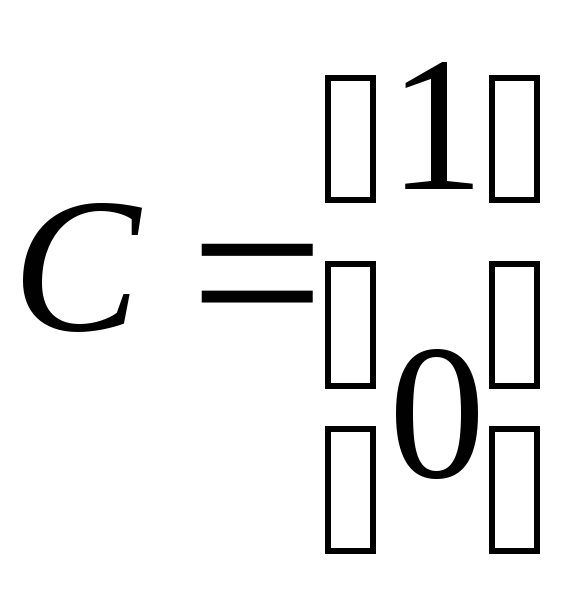 .
.
Составляем матрицу управляемости
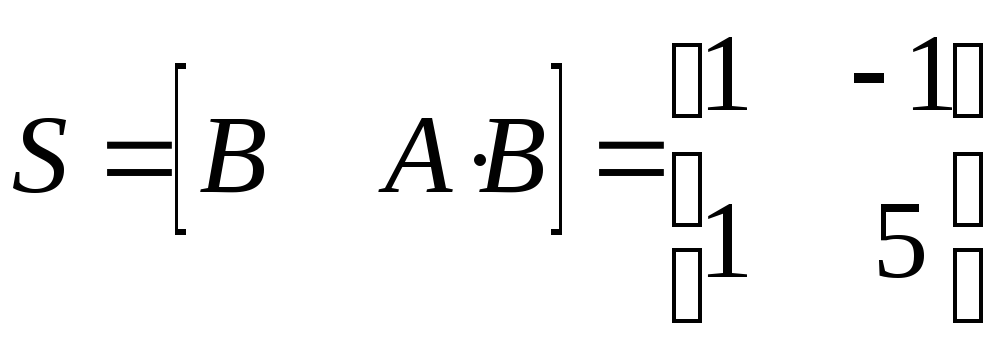 .
.
Ее
ранг равен двум![]() ,
следовательно, система обладает свойством
управляемости. Это значит, что систему
можно привести к канонической форме
управляемости.
,
следовательно, система обладает свойством
управляемости. Это значит, что систему
можно привести к канонической форме
управляемости.
Найдем
матрицу
![]() обратную к матрице
обратную к матрице![]() .
Имеем:
.
Имеем:![]()
 ,
,
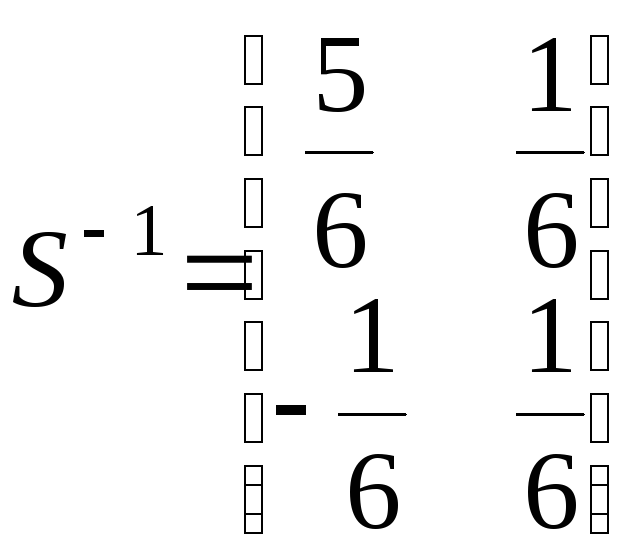
Найдем
произведение матриц
![]() :
:
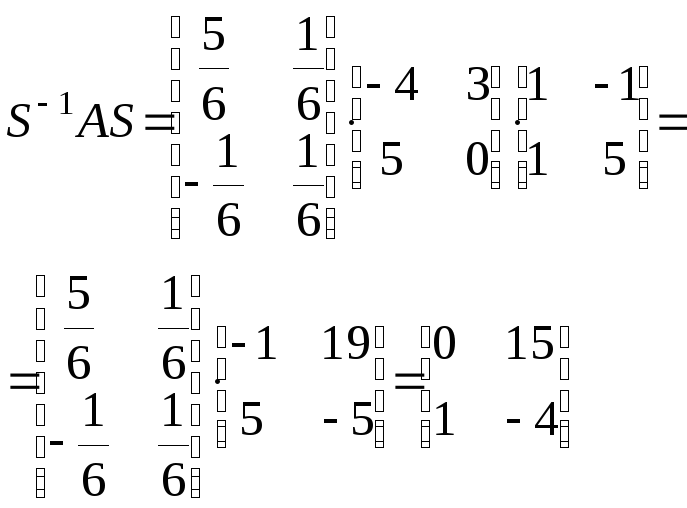
Последний столбец – коэффициенты характеристического полинома с обратными знаками. Характеристический полином
![]() ,
,
поэтому
![]() ,
,![]() .
.
Проверка.
Характеристический полином матрицы
![]() :
:
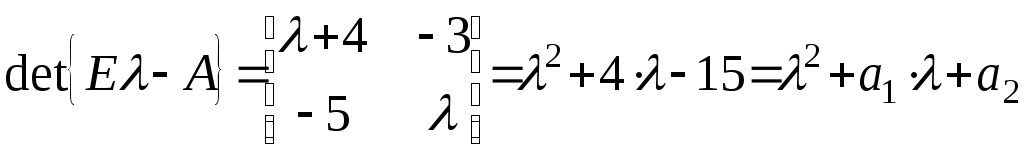 ,
,
![]() ,
,
![]() .
.
Найдем
матрицу![]() и обратную к ней
и обратную к ней![]() :
:
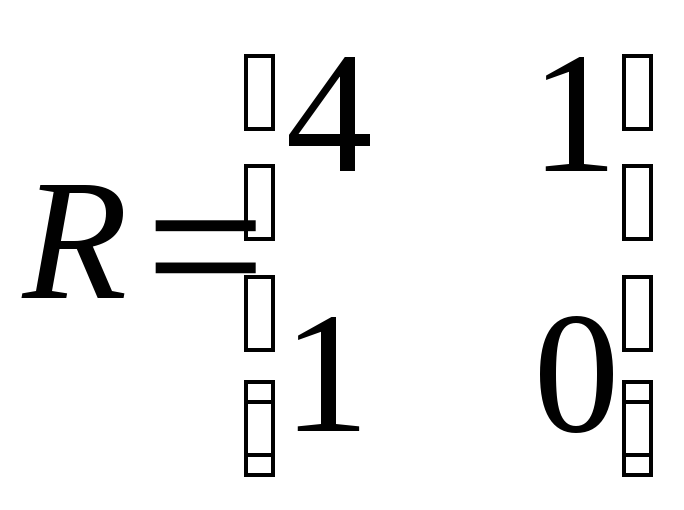 ;
;
![]() ;
;
 .
.
Матрица
преобразования к канонической форме
управляемости
![]()
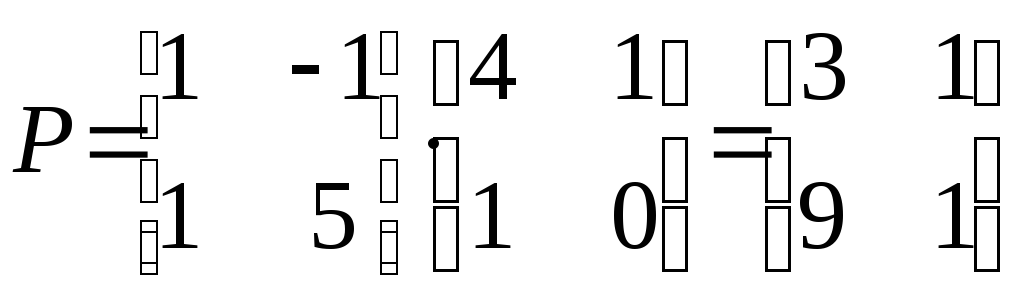 .
.
Найдем
обратную матрицу
![]() к матрице
к матрице![]() :
:
![]() ,
,
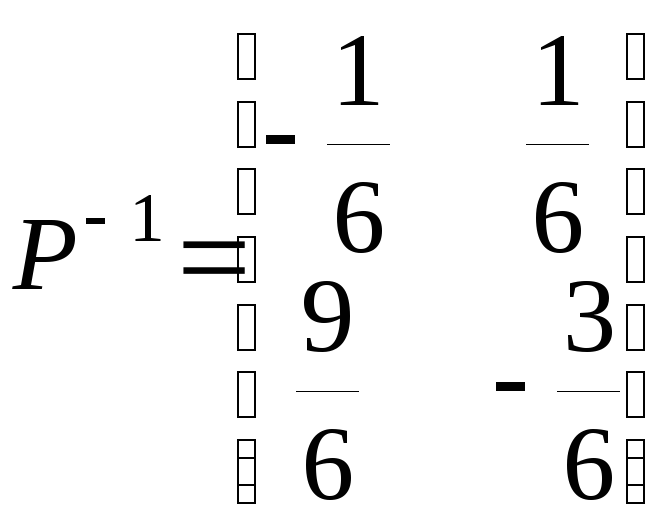 .
.
Проверка:
 ,
,
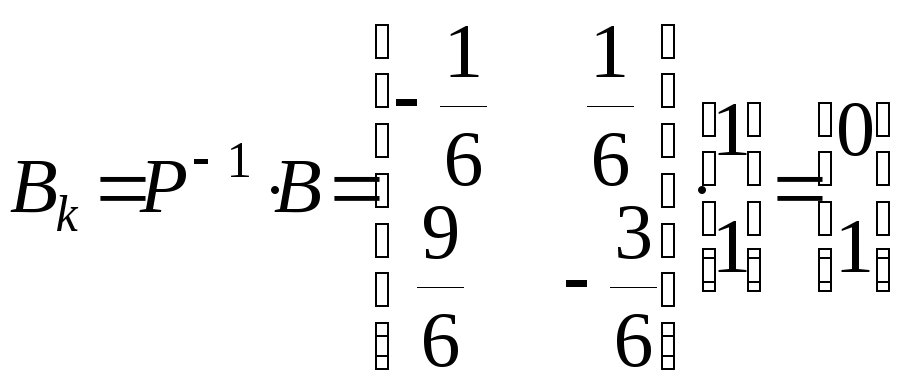 ,
,
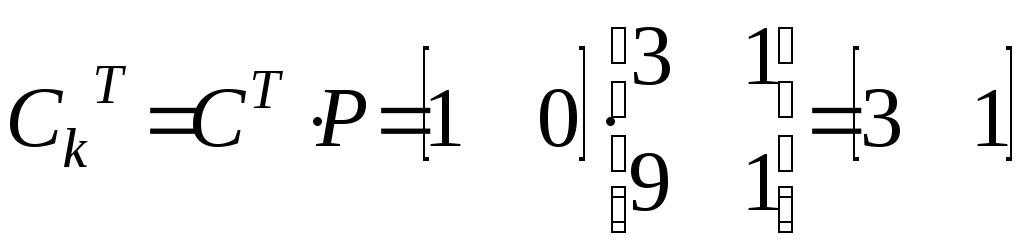 .
.
Математическая модель системы в канонической форме записи:
![]() ,
,
![]() ,
,
![]() .
.
В соответствии с этими уравнениями структурная схема системы относительно канонических переменных состояния имеет вид
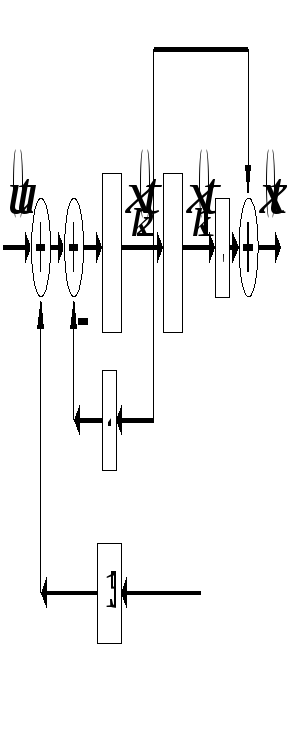
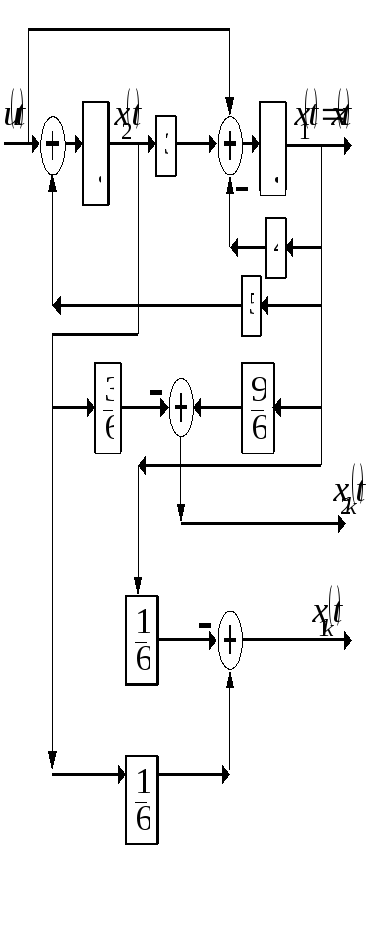
Канонические формы наблюдаемости.
Пусть математическая модель объекта управления задана системой уравнений:
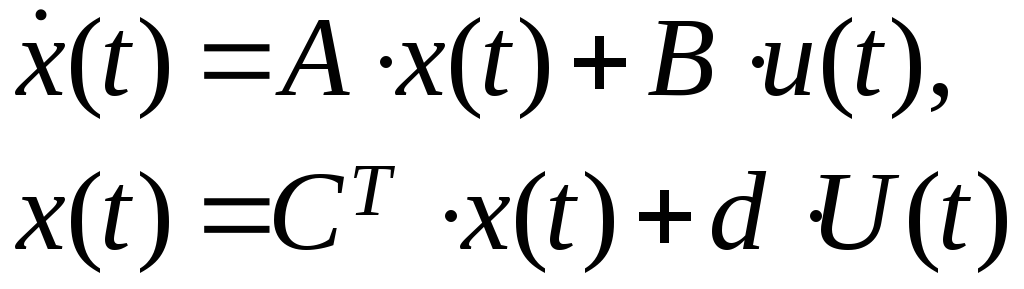 (1)
(1)
Будем говорить, что математическая модель объекта управления (1) записана в канонической форме наблюдаемости, если

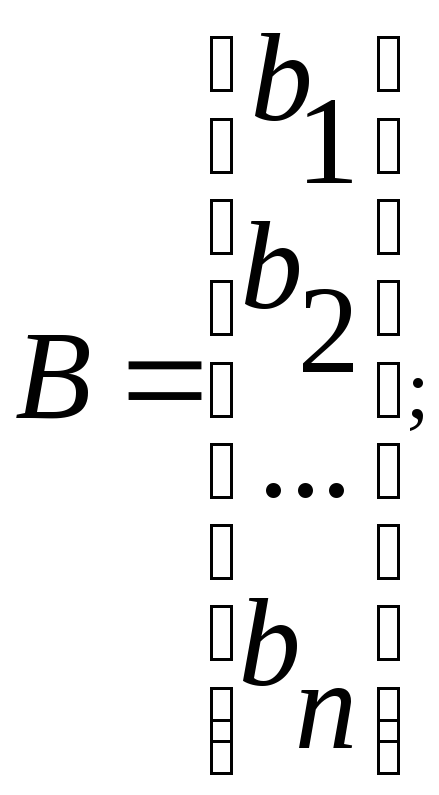
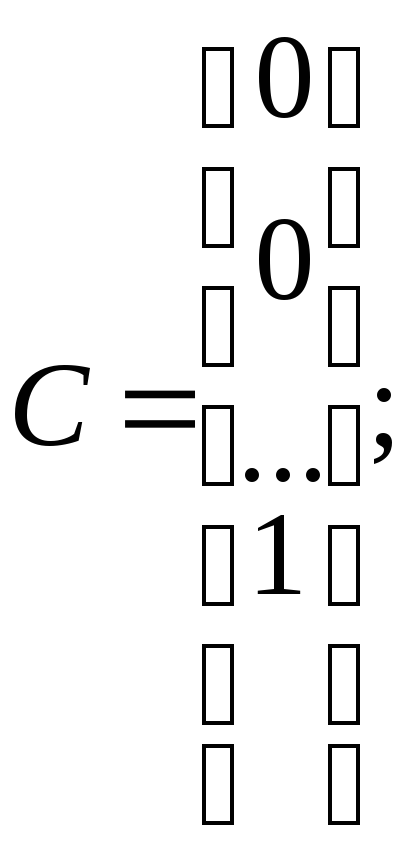
Если объект управления (1) записан в канонической форме наблюдаемости, то сопряженная ему система записана в канонической форме управляемости.
СИНТЕЗ ЛИНЕЙНЫХ СИСТЕМ УПРАВЛЕНИЯ
по заданному расположению корней характеристического
уравнения замкнутой системы.
Пусть заданна передаточная функция замкнутой системы
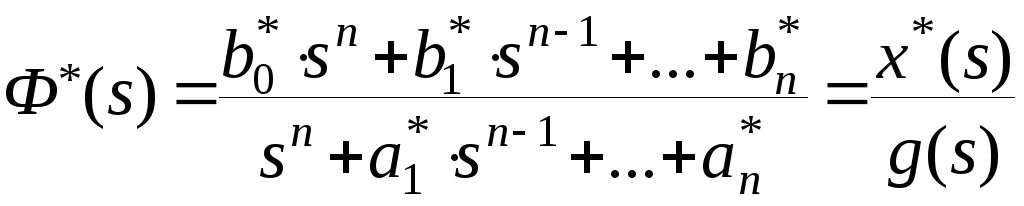 (1)
(1)
В
системе автоматического управления с
передаточной функцией
![]() процессы удовлетворяют всем заданным
требованиям, предъявленным к процессам
автоматического управления.
процессы удовлетворяют всем заданным
требованиям, предъявленным к процессам
автоматического управления.
Характеристическое уравнение замкнутой системы имеет вид
![]()
где
корни
![]() .
.
От
передаточной функции
![]() перейдём к математической модели
замкнутой системы в виде системы
дифференциальных уравнений, записанных
в нормальной форме Коши:
перейдём к математической модели
замкнутой системы в виде системы
дифференциальных уравнений, записанных
в нормальной форме Коши:
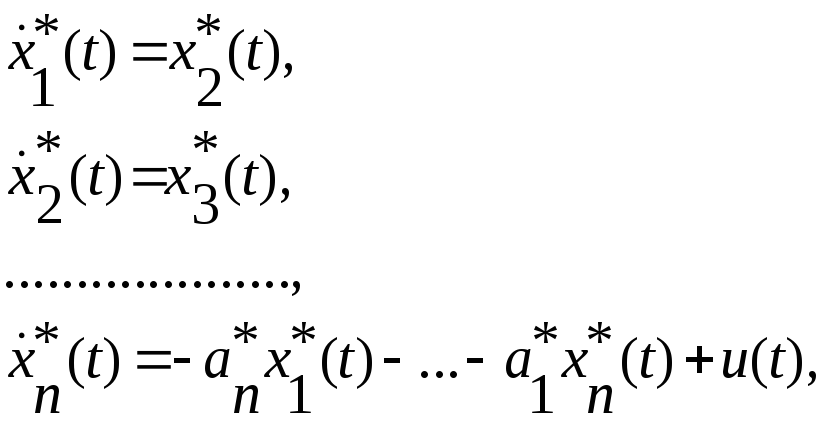 (2)
(2)
![]() (3)
(3)
Или в векторно-матричной форме записи
![]() ,
(4)
,
(4)
![]() .
(5)
.
(5)
Уравнения (2)-(3), а, следовательно, и (4),(5) имеют каноническую форму записи, каноническая форма управляемости.
Пусть далее математическая модель объекта управления задана в виде передаточной функции
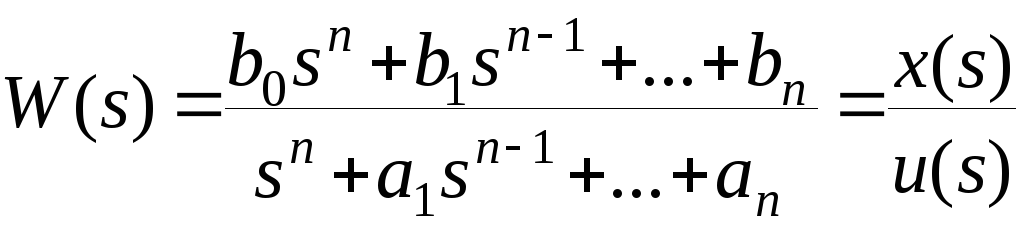 . (6)
. (6)
От
передаточной функции
![]() перейдём к математической модели объекта
управления относительно переменных
состояния, имеем
перейдём к математической модели объекта
управления относительно переменных
состояния, имеем
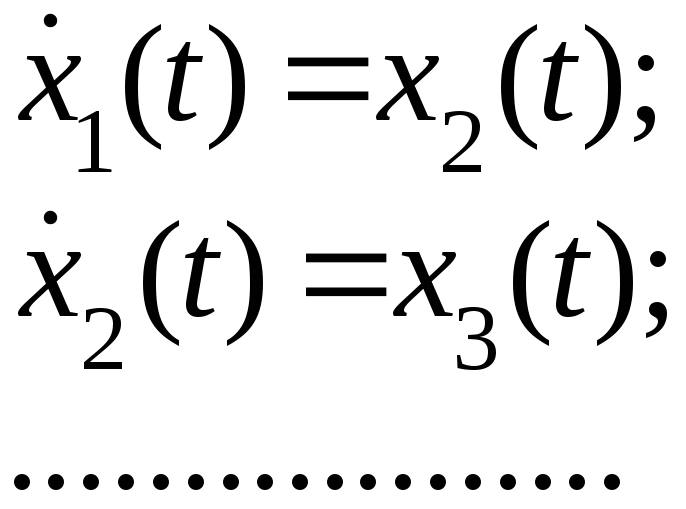 (7)
(7)
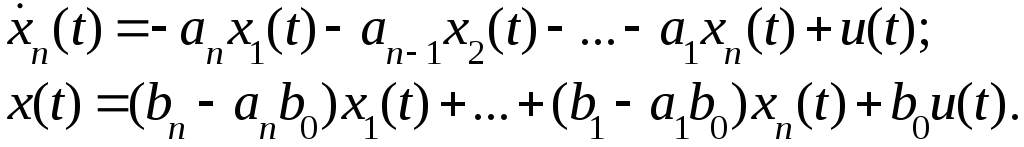 (8)
(8)
