Принцип дуальности управляемости и наблюдаемости.

Р.Каманом был установлен следующий принцип двойственности (принцип дуальности): пусть даны две системы, из которых одна описывается уравнениями

,

, (*)

а другая уравнениями

,

. (**)

Такие системы называются двойственными или сопряженными друг к другу. Очевидно, что условие

является условием управляемости системы (*) и одновременно условием наблюдаемости системы (**), а равенство

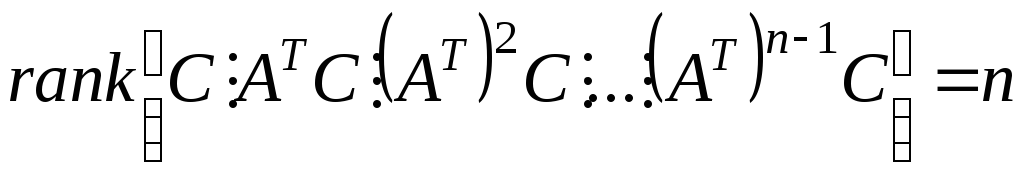
условием наблюдаемости системы (*) и одновременно условием управляемости системы (**). Иными словами, система (*) управляема тогда и только тогда, когда наблюдаема сопряженная с ней система (**) и наоборот.

Пример. Структурная схема динамического объекта управления имеет вид

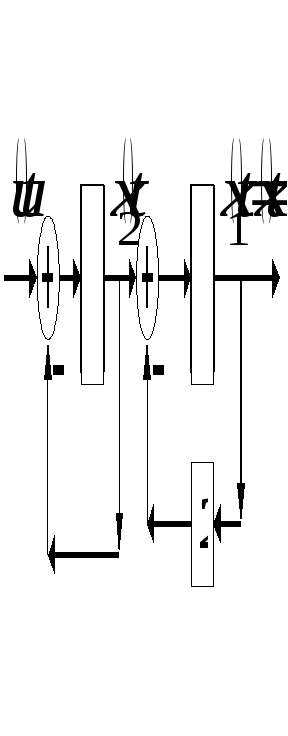
Исследовать наблюдаемость объекта управления.

Решение. Дифференциальные уравнения, описывающие процессы в объекте управления в соответствии со структурной схемой будут

,

,

.

Тогда:

, ,,.

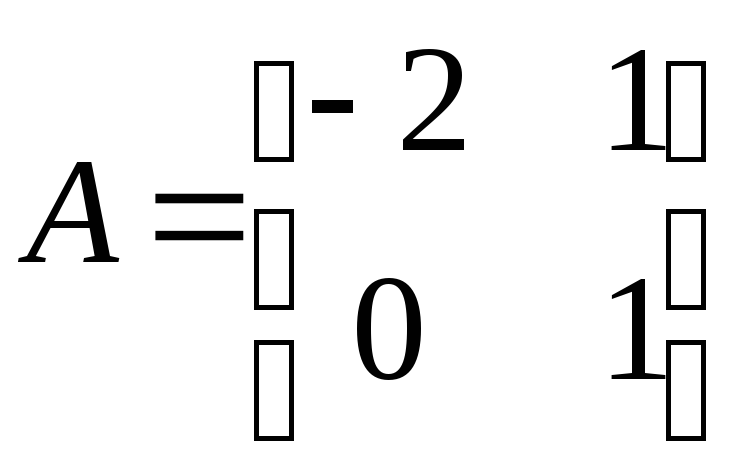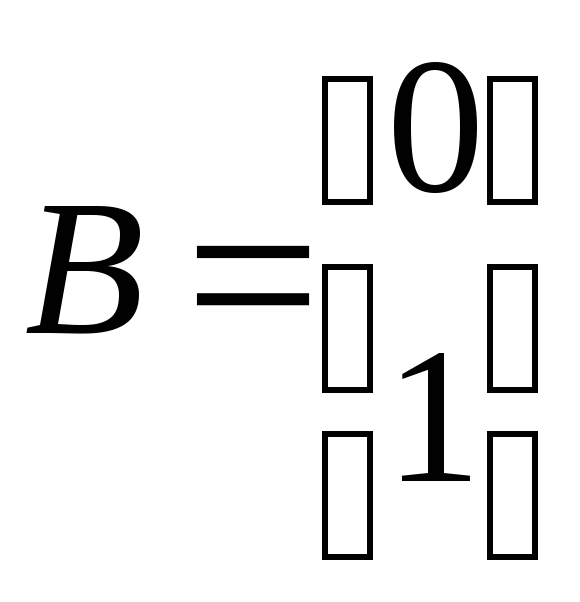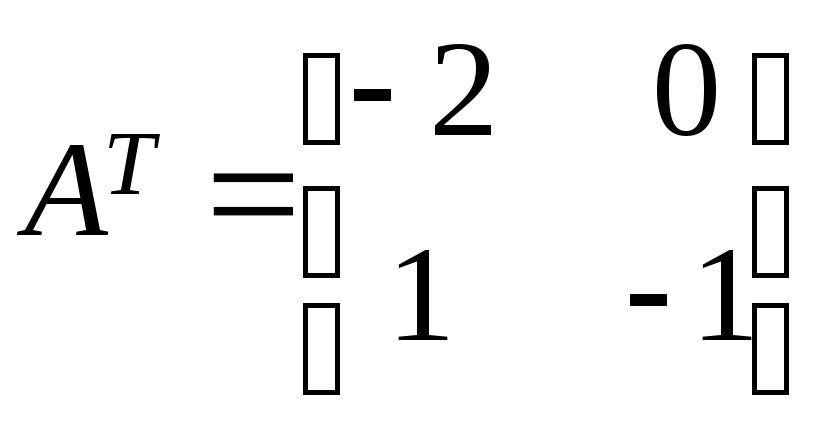Составим матрицу наблюдаемости:

, ,,

.

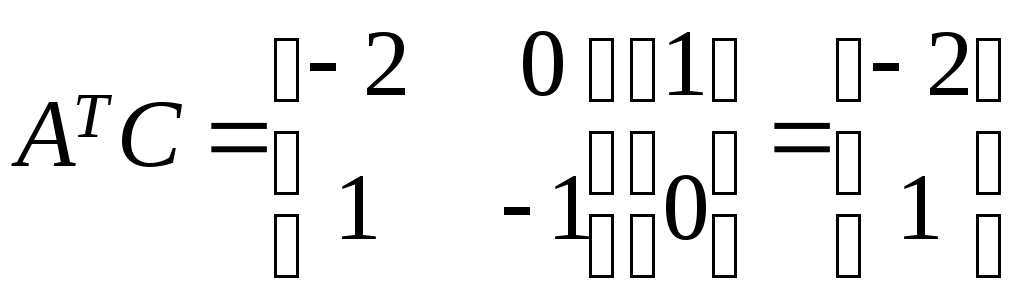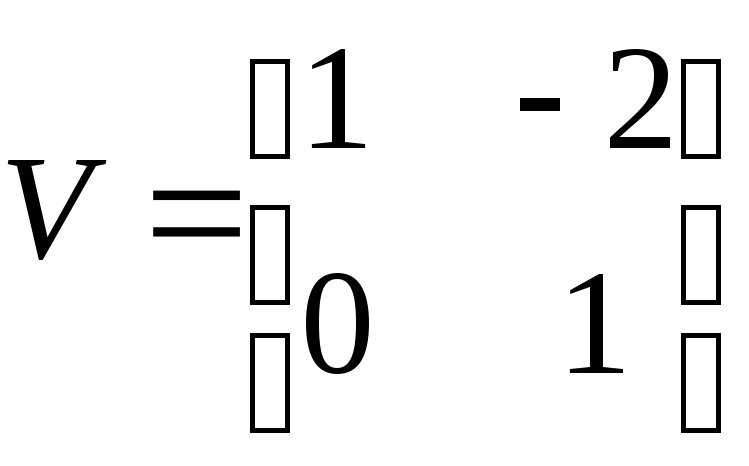Система наблюдаема.

КАНОНИЧЕСКАЯ ФОРМА УПРАВЛЯЕМОСТИ.

Пусть передаточная функция объекта управления имеет вид

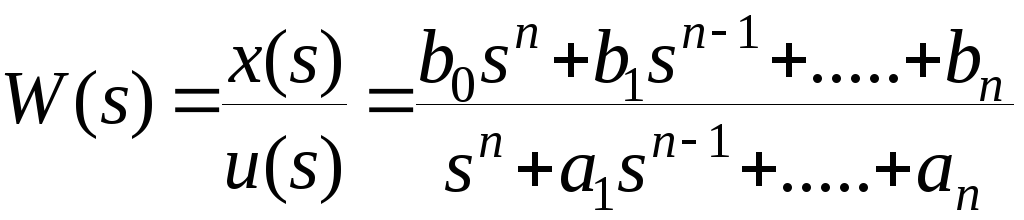
От математической модели динамического объекта в форме передаточной функции перейдем к его математической модели в виде дифференциальных уравнений:

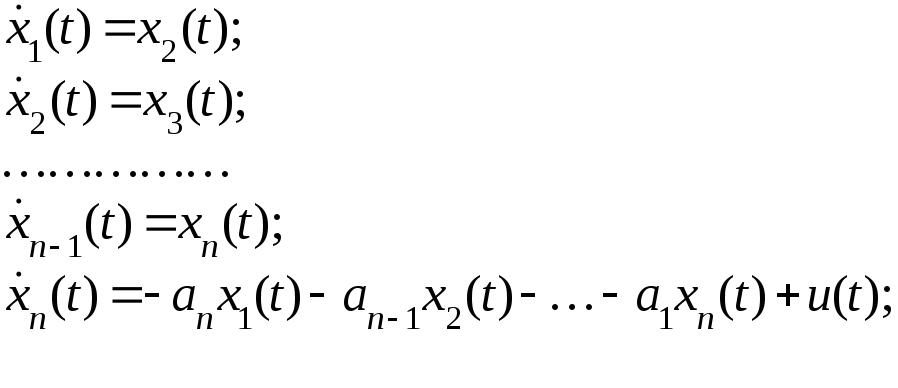(1)

и уравнения выхода:

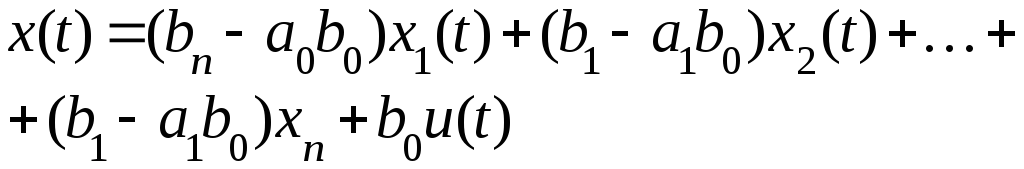. (2)

Такая форма записи математической модели динамического объекта управления называется канонической формой управляемости при этом:

, ,

, .

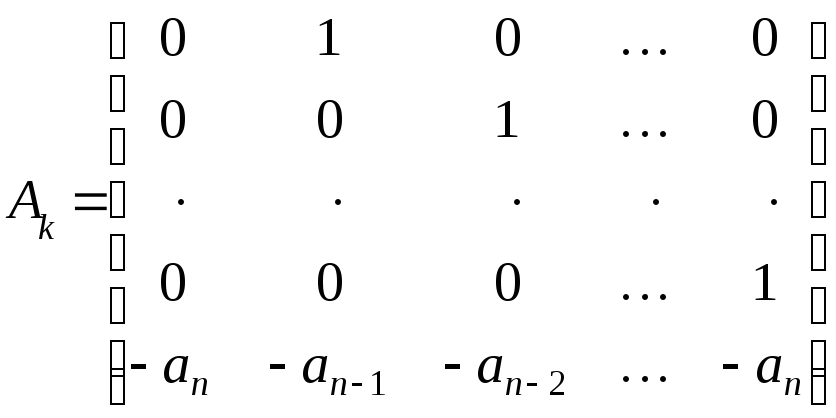Замечание 1. Последняя строка матрицы составлена из коэффициентов характеристического уравнения математической модели динамического объекта управления.

Замечание 2. Динамический объект управления, математическую модель которого можно привести к виду (1), (2), всегда обладает свойством управляемости. Это легко проверить непосредственным вычислением ранга матрицы управляемости

. (3)

Пусть задан динамический объект управления, математическая модель имеет вид

, (4)

где матрица динамики объекта управления и вектор – произвольного вида.

Если объект управления (4) обладает свойством управляемости, то его математическую модель можно преобразовать к канонической форме записи (1) и (2) с помощью невырожденного преобразования

, (5)

где матрица преобразования определяется с помощью равенства

, (6)

где – матрица управляемости для математической модели объекта управления (4); – матрица управляемости вида (3).

Было доказано, что матрица определяется с помощью равенства

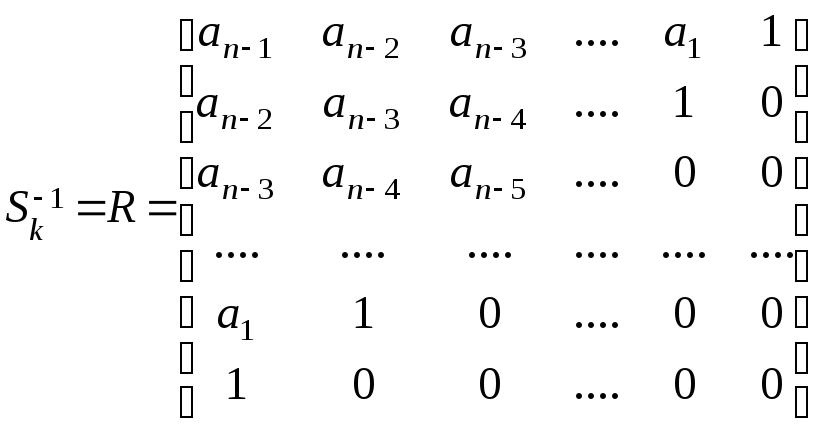, (7)

где - коэффициенты характеристического полинома матрицы динамики объекта управления:

. (8)

Таким образом, определив матрицу преобразования с помощью равенства

(9)

и учитывая, что

(10)

получим следующее соотношения, определяющие и:

, (11)

. (11.а)

Из выше сказанного следует, что преобразование математической модели объекта управления (4) к канонической форме записи полностью определяется матрицей динамики объекта управления и вектора .

Наиболее трудоемкой операцией в алгоритме преобразования (4) к канонической форме записи – это получение коэффициентов характеристического уравнения (8). Известны различные способы вычисления коэффициентов характеристического полинома матрицы . Однако в данном случае целесообразно воспользоваться равенством

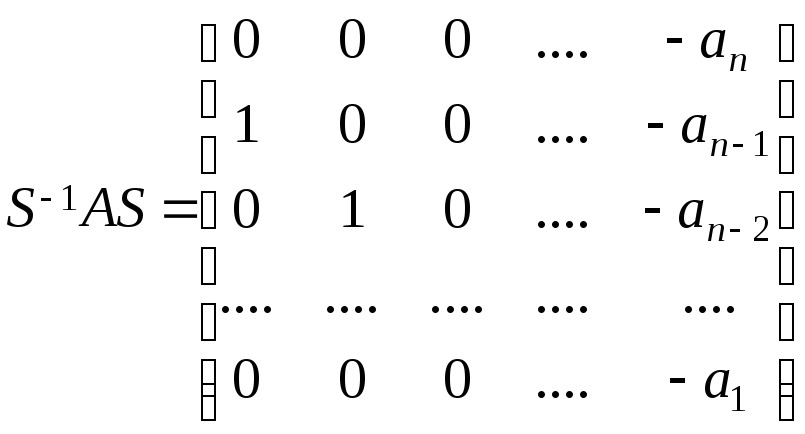, (12)

т. е. произведение – образует матрицу, у которой элементы последнего столбца – коэффициенты характеристического полинома матрицы , взятые с обратным знаком.

Алгоритм

преобразования математической модели

динамического объекта к канонической форме записи.

Исходные данные: Матрица динамики объекта управления , вектор .

<1> Составляется матрица управляемости объекта управления

<2> Проверить выполнение критерия управляемости .

<3> Вычислить коэффициенты характеристического полинома матрицы

(с помощью равенства (12)).

<4> Сформировать матрицу R.

<5> Вычислить матрицу преобразования исходной математической модели (4) к канонической форме записи (1), (2):

<6> Вычислить , , .

Пример. (Преобразование к канонической форме управляемости с помощью < матриц управляемости >.) Дана система автоматического управления, структурная схема которой показана на рисунке

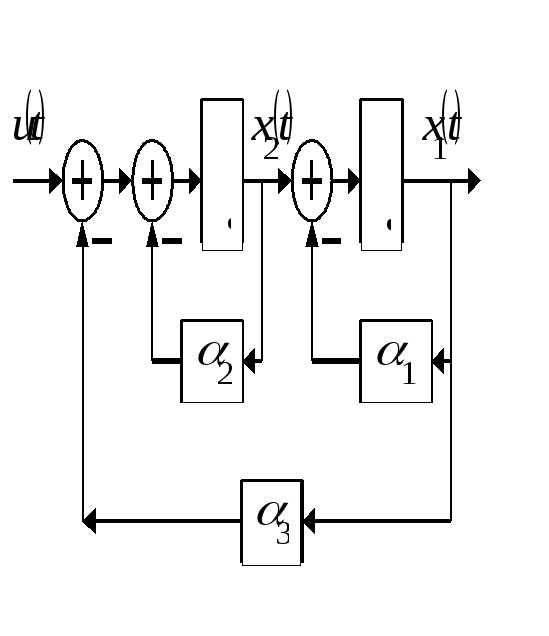
Привести математическую модель системы к канонической форме записи. Преобразование выполнить при следующих значениях параметров исходной системы , , .

Решение. Составим дифференциальное уравнение системы:

,

,

.

; ; ; .

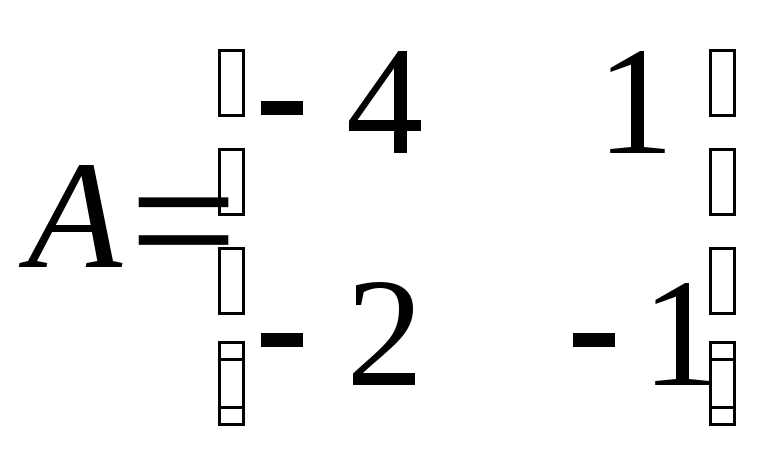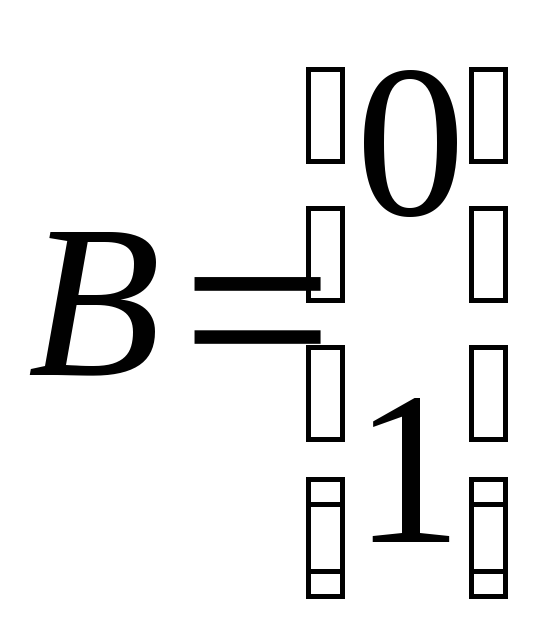<1> Матрица управляемости:

, , , .

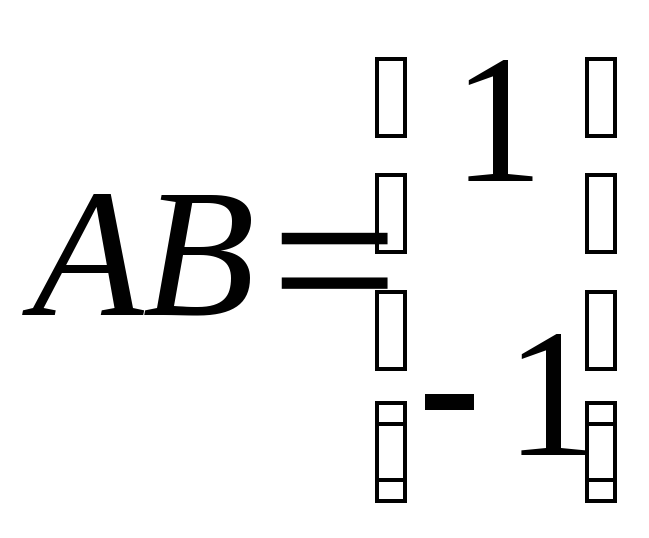Исходная система управляема.

<2> Характеристический полином матрицы :

;

; ;

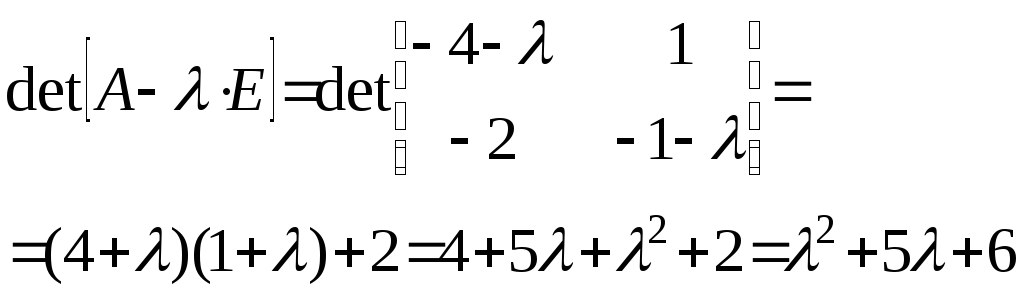<3> ; .

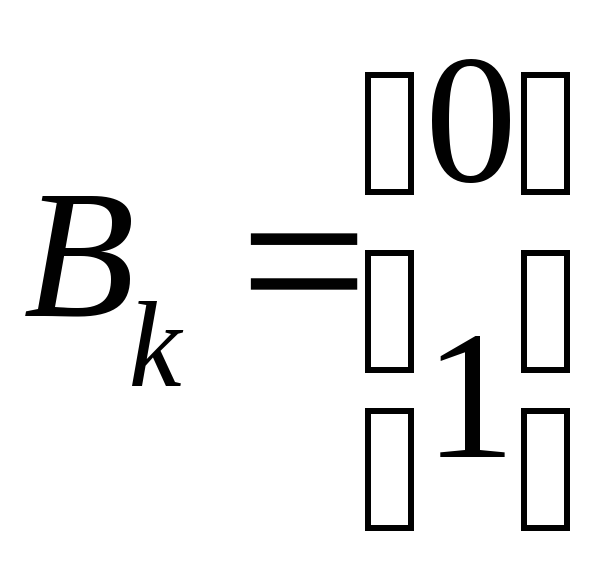<4> .

<5> .

.

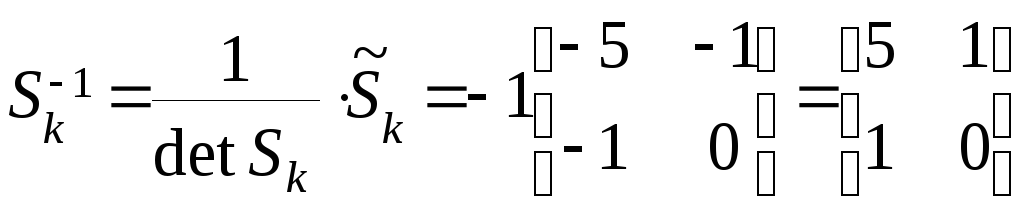<6> Вычисление матриц и

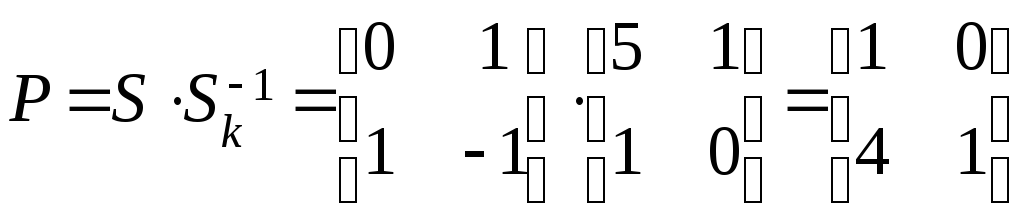
Проверка: ; .

;

.

,
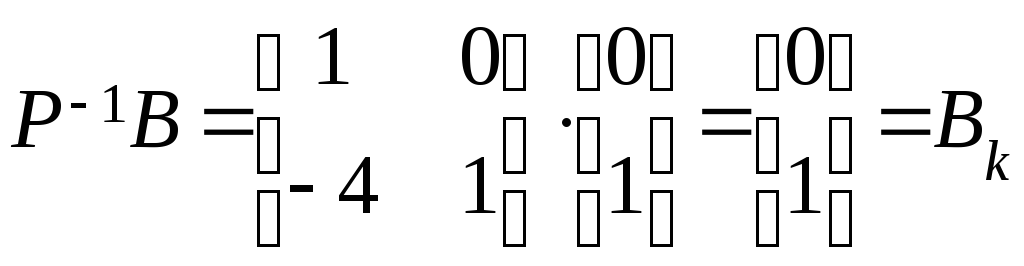
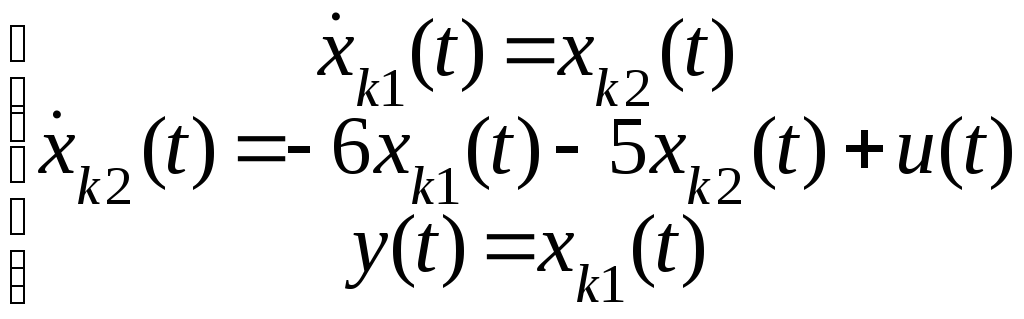