
- •Лабораторный практикум
- •Введение
- •Лабораторная работа №1 Динамические звенья систем автоматического управления
- •Моделирование звеньев в среде ewb 5.12
- •Лабораторная работа №2 Статические и астатические сау
- •Лабораторная работа №3 Последовательные корректирующие устройства
- •Исследование статических и динамических свойств объекта управления
- •Исследование статических и динамических свойств замкнутой системы управления с пропорциональным регулятором
- •3. Исследование статических и динамических свойств замкнутой
- •4. Исследование статических и динамических свойств замкнутой
- •5. Исследование статических и динамических свойств замкнутой
- •Лабораторная работа №4 Синтез корректирующих устройств по критериям модульного, симметричного и компромиссного оптимумов.
- •1. Критерий модульного оптимума (мо)
- •2. Критерий симметричного оптимума (со)
- •3. Критерий компромиссного оптимума (ко)
- •Лабораторная работа №5 Синтез регуляторов методами модального управления
- •Контрольные вопросы и задачи
- •13.24. Модель объекта описывается передаточной функцией вида
- •Рассчитать параметры регулятора модальным методом синтеза по требованиям к качеству переходных процессов: с,
- •13.25. Модель объекта заданна системой уравнений
Контрольные вопросы и задачи
Пример 13.1. Проверить свойство управляемости для объекта, модель которого задана системой дифференциальных уравнений вида:

Решение. Определим матрицу коэффициентов системы (А) и матрицу входа (В)

Порядок системы
равен 3, следовательно, матрица
управляемости имеет вид
![]() .
.
Вычислим матрицы произведений
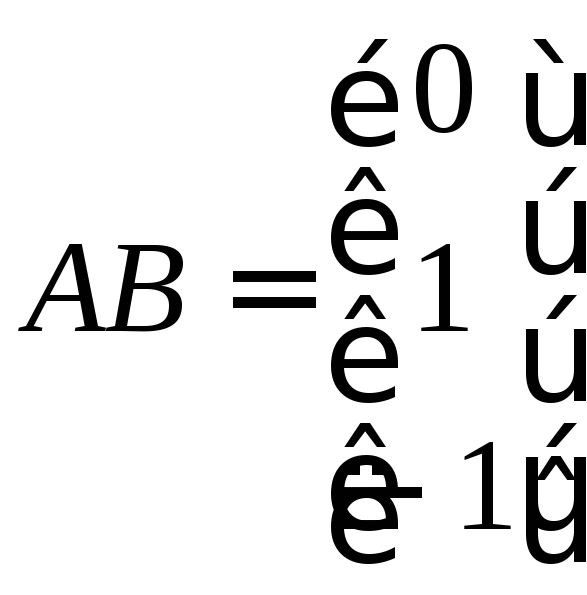 ,
,
 .
.
Составим матрицу управляемости
 ,
,
ее определитель
равен
![]() ,
следовательно, объект управляем.
,
следовательно, объект управляем.
13.1. Проверить свойство управляемости для объекта, модель которого задана системой дифференциальных уравнений вида:
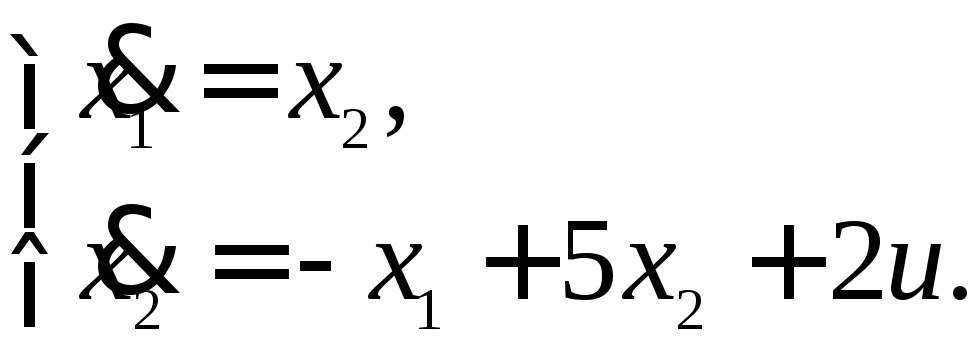
13.2. Проверить свойство управляемости для объекта, модель которого задана системой дифференциальных уравнений вида:
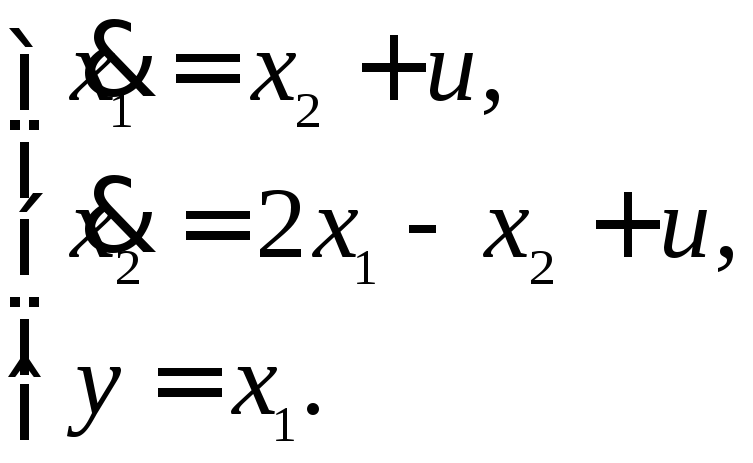
Найти передаточную функцию модели объекта, вычислить нули и полюса.
13.3. Проверить свойство управляемости для объекта, модель которого задана системой дифференциальных уравнений вида:
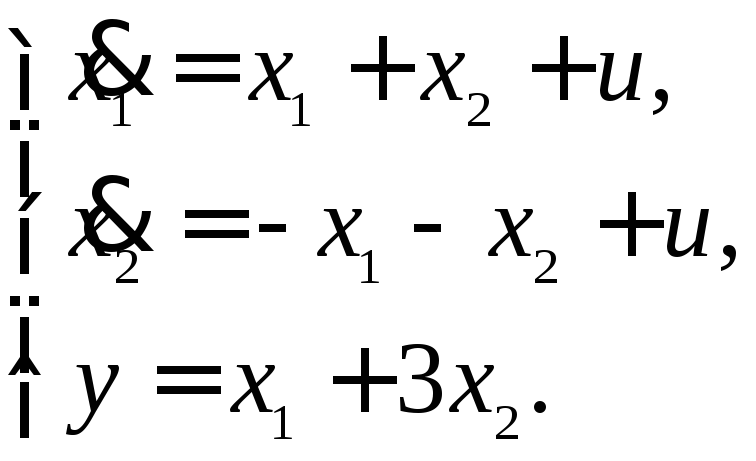
Найти передаточную функцию модели объекта, вычислить нули и полюса.
13.4. Проверить свойство управляемости для объекта, модель которого задана системой дифференциальных уравнений вида:
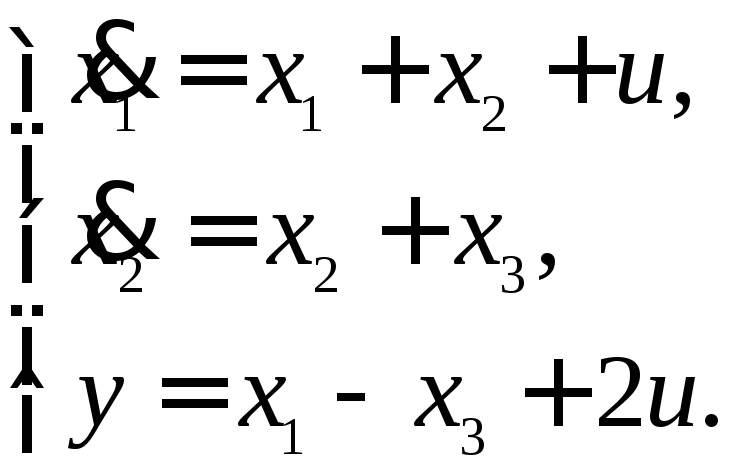
13.5. Модель объекта управления задана передаточной функцией:
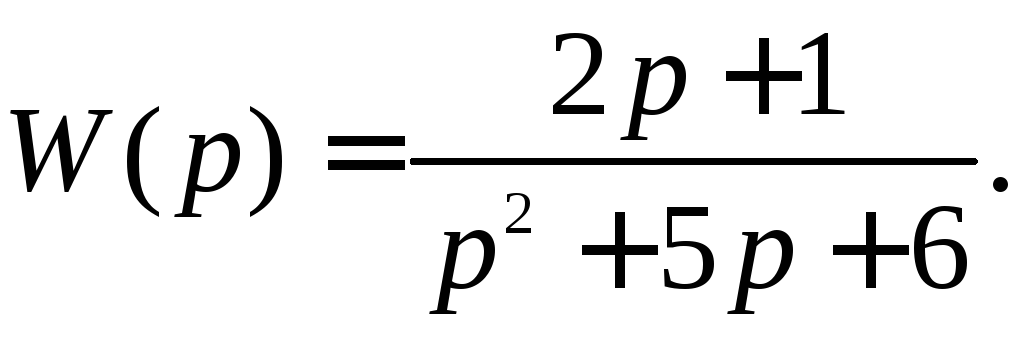
Записать уравнения модели в форме Коши, проверить свойство управляемости.
13.6. Модель объекта управления задана передаточной функцией:
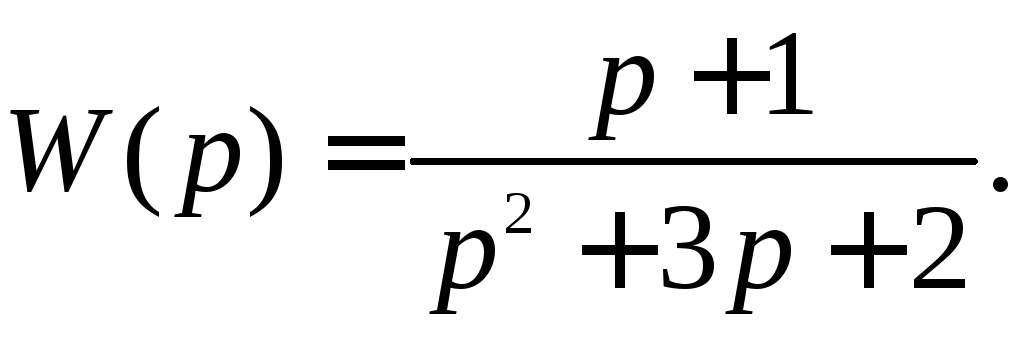
Записать уравнения модели в форме Коши, проверить свойство управляемости.
13.7. Уравнения состояний системы имеют вид:
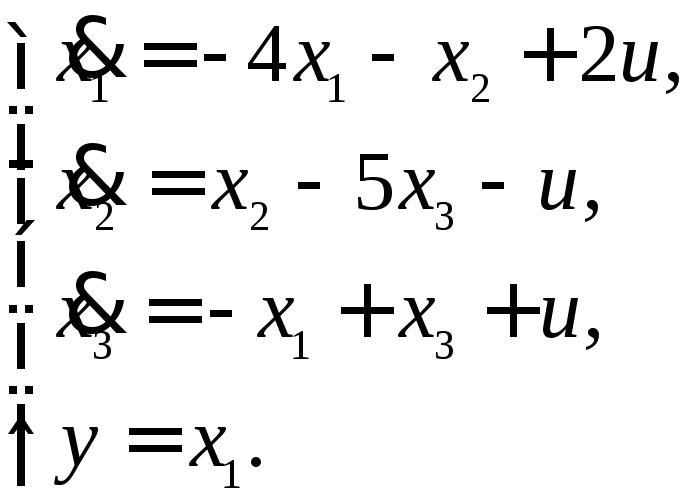
Проверить свойство управляемости объекта.
13.8. Модель объекта описывается передаточной функцией:
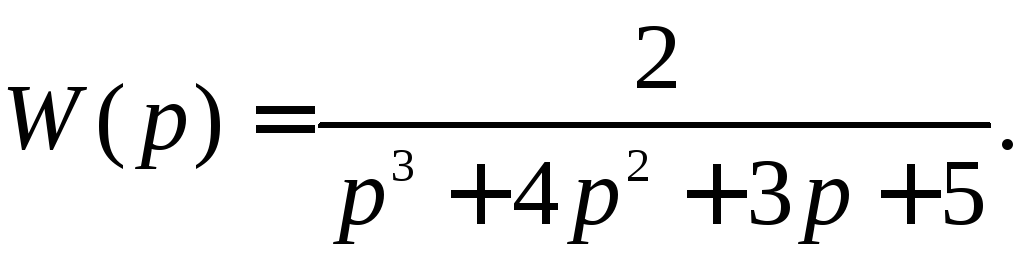
Проверить управляемость объекта.
13.9. Модель объекта описывается передаточной функцией:

Проверить управляемость объекта.
13.10. Дана структурная схема объекта:
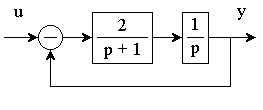
Рис. 13.9
Проверить управляемость объекта.
13.11. Модель линейного объекта задана матрицами АВС следующего вида:
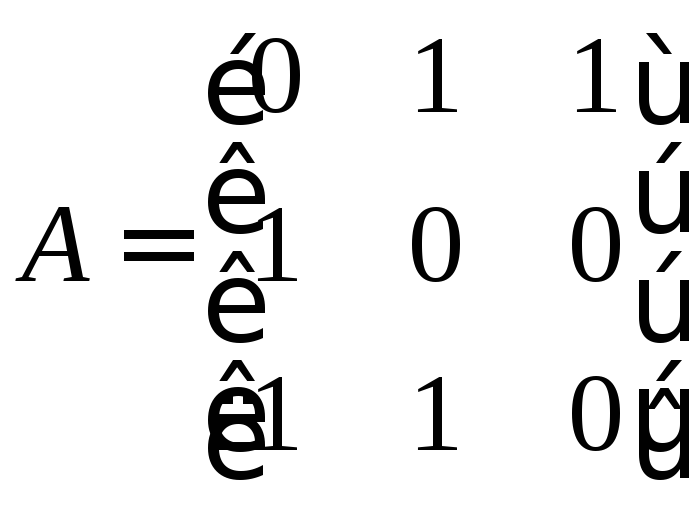 ;
;
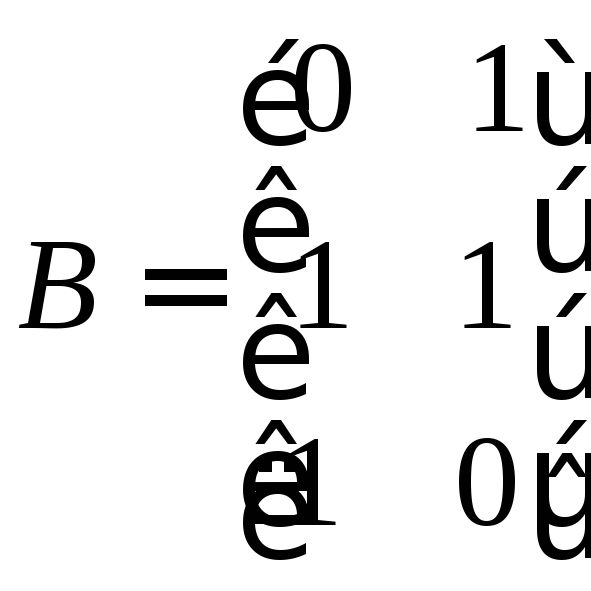 ;
;
![]() .
.
Проверить управляемость объекта.
13.12. Даны уравнения состояний системы:
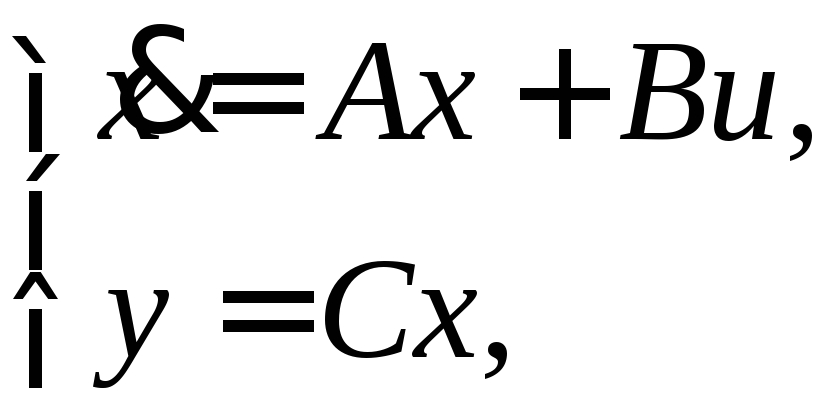
![]()
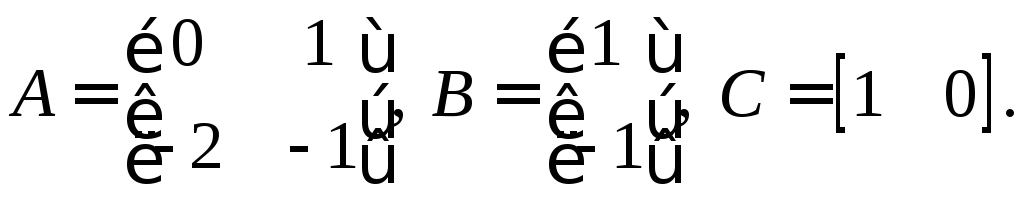
Проверить свойство управляемости объекта.
Пример 13.2. Модель объекта управления имеет вид
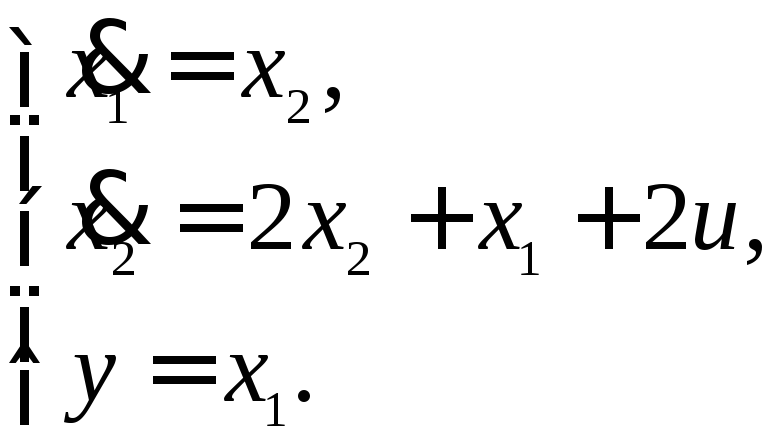 (14.1)
(14.1)
Требуется вычислить параметры закона управления на основе матричной процедуры модального метода синтеза, обеспечивающего выполнение следующих условий:
![]()
![]()
Решение. Закон управления для объекта второго порядка имеет вид
![]() ,
(14.2)
,
(14.2)
где
![]() –
неизвестные коэффициенты (параметры
регулятора), значение которых необходимо
определить.
–
неизвестные коэффициенты (параметры
регулятора), значение которых необходимо
определить.
Подставив уравнение (14.2) в (14.1), получим систему уравнений, которая описывает замкнутую систему:
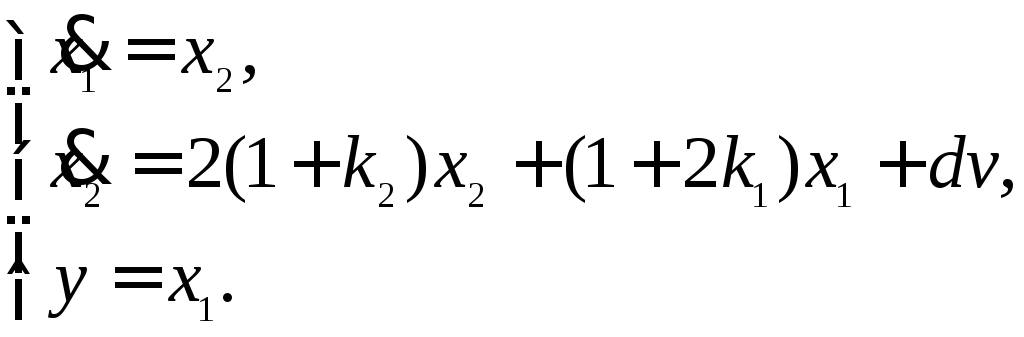
Матрицы коэффициентов системы равны
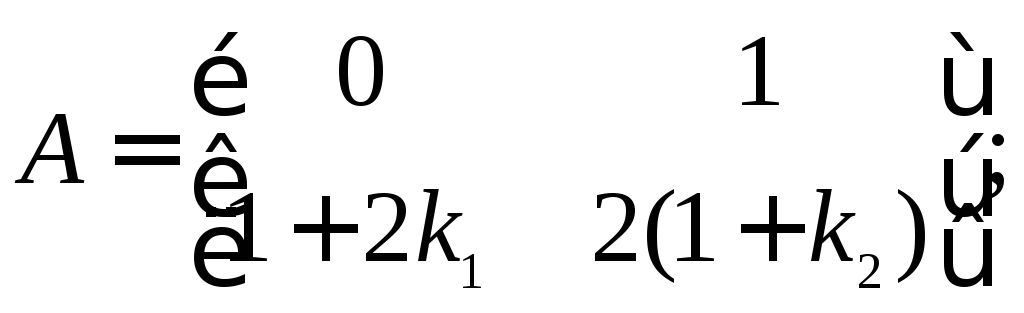
 ;
;
![]() .
.
Определим характеристический полином системы
![]() (14.3)
(14.3)
Неизвестные
коэффициенты
![]() и
и
![]() можно определить из равенства (14.3)
полиному желаемого вида (
можно определить из равенства (14.3)
полиному желаемого вида (![]() ).
На основе значения
).
На основе значения
![]() и
и
![]() найдем область допустимого расположения
корней замкнутой системы. Порядок
системы равен 2, поэтому выбираем из
области два корня, например,
найдем область допустимого расположения
корней замкнутой системы. Порядок
системы равен 2, поэтому выбираем из
области два корня, например,
![]()
Находим желаемый полином:
![]() (14.4)
(14.4)
Приравняв коэффициенты полиномов (14.3) и (14.4) при одинаковых степенях р, имеем
![]()
![]() .
.
Из условия статики:
![]() ,
определим неизвестный коэффициент
,
определим неизвестный коэффициент
![]() .
.
Уравнение регулятора имеет вид
![]()
Пример 13.3. Для объекта модель которого имеет вид
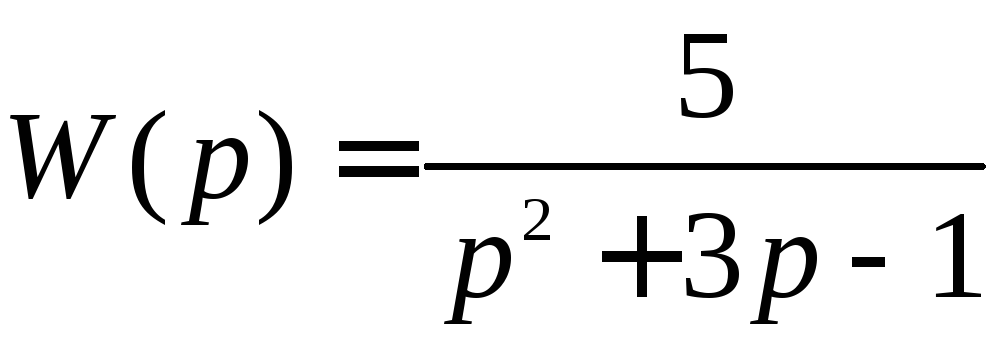 ,
,
рассчитать параметры
регулятора , используя операторную
процедуру модального метода синтеза.
Требования к качеству процессов в
системе следующие:
![]() с;
с;
![]()
![]()
Решение. Расчетная структурная схема замкнутой системы
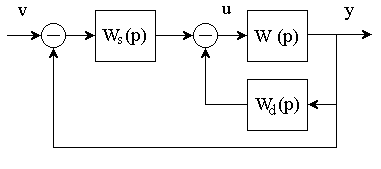
Рис. 13.10
где
![]() –
составляющая регулятора, обеспечивающая
нулевую статическую ошибку;
–
составляющая регулятора, обеспечивающая
нулевую статическую ошибку;
![]() –
составляющая регулятора, обеспечивающая
динамические свойства; (
–
составляющая регулятора, обеспечивающая
динамические свойства; (![]() )
– неизвестные коэффициенты.
)
– неизвестные коэффициенты.
Запишем характеристическое уравнение замкнутой системы
![]()
или
![]()
Сформируем желаемое характеристическое уравнение 3 – го порядка,
выбрав распределение корней обеспечивающее заданное качество процессов
![]()
![]()
![]()
Получим желаемое характеристическое уравнение
![]()
или
![]()
Приравнивая коэффициенты при соответствующих степенях оператора р, получим расчетные соотношения
![]()
![]()
![]()
Отсюда находим параметры регулятора
![]()
![]()
![]()
13.13. Заданы требования к переходным процессам в системе в целом:
![]()
Записать желаемое характеристическое уравнение третьего порядка.
13.14. Заданы требования к переходным процессам в системе в целом:
![]()
Записать желаемое характеристическое уравнение.
13.15.
Составить модель системы стабилизации
второго порядка, качество процессов в
которой удовлетворяли следующим
требованиям:
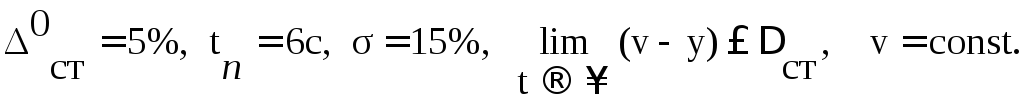
13.16.
Записать желаемый характеристический
полином четвертого порядка по заданным
показателям качества процессов:
![]()
13.17.
Записать желаемый характеристический
полином третьего порядка по заданным
показателям качества процессов:
![]()
13.18. Для объекта, модель которого задана передаточной функцией
![]()
заданы требования
к переходным процессам в системе в
целом:
![]()
Рассчитать параметры регулятора модальным методом синтеза.
13.19. Для объекта, модель которого описывается передаточной функцией
![]()
Заданы требования
к переходным процессам в системе в
целом:
![]() Найти параметры регулятора модальным
методом синтеза.
Найти параметры регулятора модальным
методом синтеза.
13.20. Модель объекта управления имеет вид
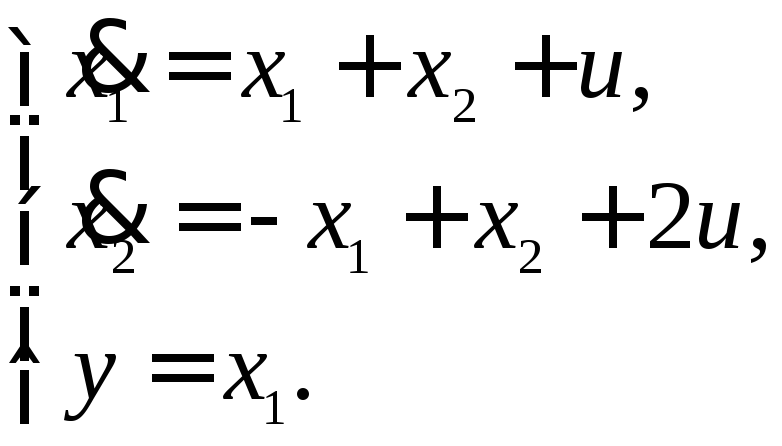
Заданы требования
к переходным процессам в системе в
целом:![]() Рассчитать параметр регулятора модальным
методом синтеза.
Рассчитать параметр регулятора модальным
методом синтеза.
13.21 Модель объекта управления имеет вид:
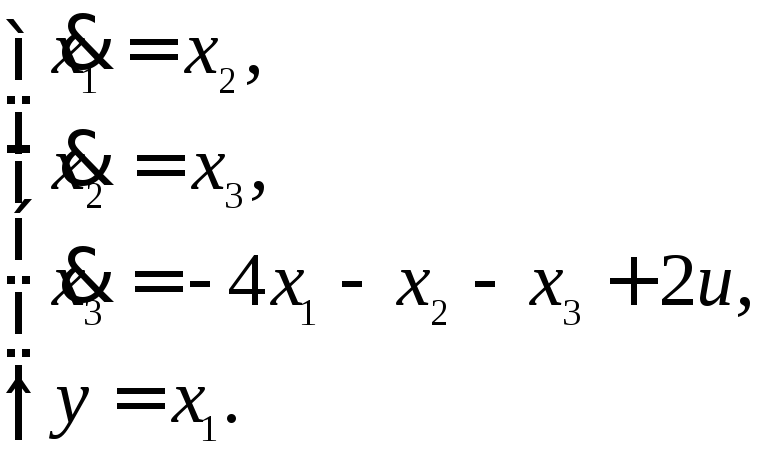
Заданы требования
к переходным процессам в системе в
целом:
![]() Вычислить параметры регулятора модальным
методом синтеза.
Вычислить параметры регулятора модальным
методом синтеза.
13.22. Модель объекта управления имеет вид:
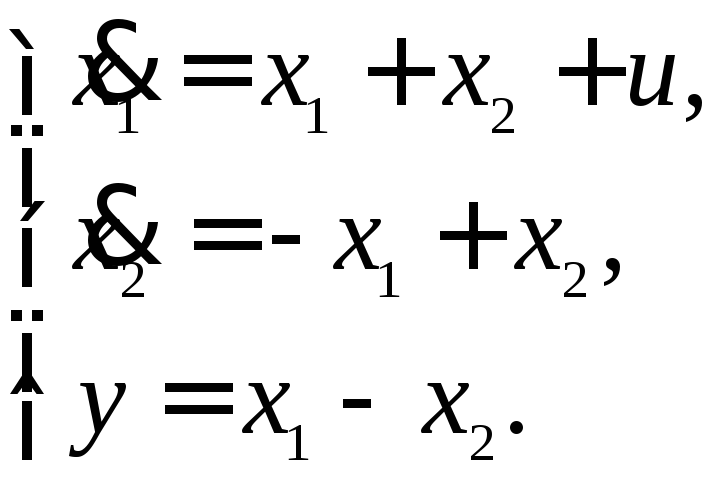
Рассчитать параметры
регулятора модальным методом синтеза.
Обеспечить требования:
![]() с,
с,
![]()
13.23.
Задан объект, поведение которого
описывается передаточной функцией вида
![]() Рассчитать
параметры регулятора модальным методом
так, чтобы качество переходных процессов
в замкнутой системе соответствовало
следующим оценкам:
Рассчитать
параметры регулятора модальным методом
так, чтобы качество переходных процессов
в замкнутой системе соответствовало
следующим оценкам:
![]() с,
с,![]()
