Пример. Каков индекс разбиения и мощности классов эквивалентности по отношению , если – отношение равенства (тождества) на любом множестве;

Ответ: Все классы эквивалентности по отношению равенства на любом множестве состоят из одного элемента. Индекс разбиения по отношению равенства равен мощности множества, т.е. .

Пример. Каков индекс разбиения и мощности классов эквивалентности по отношению , если – отношение «иметь один и тот же остаток от деления на 5» на множестве натуральных чисел .

Ответ: Индекс разбиения множества по заданному отношению R равен 5. Множества натуральных чисел, составляющие каждый класс эквивалентности, счетны.

1.2.4. Операции над бинарными отношениями

Так как отношения на задаются подмножествами , то для них определены все те же операции, что и для множеств, т.е. объединение, пересечение, дополнение, разность. Кроме того, над отношениями определены и некоторые другие операции.

Обратное отношение .

Отношение имеет место тогда и только тогда, когда имеет место . Соответственно, .

Пример. Если – «быть моложе», то – быть старше ; если – «быть подчиненным, то – быть начальником”.

Пример. Пусть ={1,2,3,4,5}, ={6,7,8,9}, ={10,11,12,13}. Пусть определены следующим образом: ={(1,7), (4,6), (5,6), 2,8)}, ={(6,10), (6,11), (7,10), (8,13)}. Определить отношения .

Ответ: ={(7,1), (6,4), (6,5), (8,2)}, ={10,6), (11,6), (10,7), (13,13)}

Составное отношение (композиция) .

Пусть заданы множества и отношения . Составное отношение действует из в посредством , и из в посредством .

Составное отношение может быть определено и на одном множестве. В частности, если , то составное отношение .

Пример: если – «быть сыном», то – «быть внуком».

Транзитивное замыкание .

Транзитивное замыкание состоит из таких, и только таких пар элементов из , для которых в существует цепочка из элементов , , , между соседними элементами которой выполняется , т.е.

.

Например, если – отношение «быть сыном», то – «быть прямым потомком».

Если отношение транзитивно то .

Пример. Пусть – отношение «быть руководителем» на множестве . Определить . Каковы свойства отношений?

– «не быть руководителем»,

– «быть подчиненным»,

– «быть руководителем», так как R – транзитивно.

Отношение – «быть руководителем»:

• не является рефлексивным, так как выражение «быть руководителем по отношению к самому себе» вряд ли имеет смысл;

• антирефлексивно, так как ни для какого члена организации не выполняется « – руководитель »;

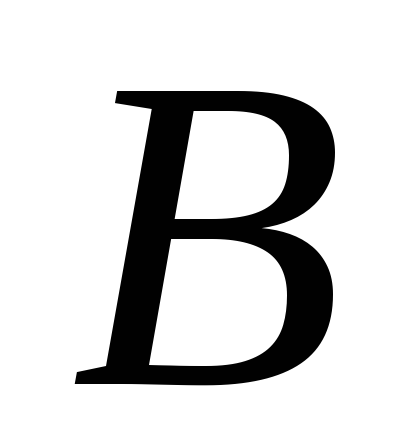• не симметрично, т.к. если – руководитель , то 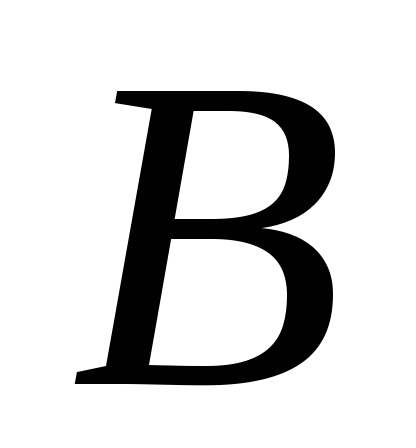не может быть руководителем ;

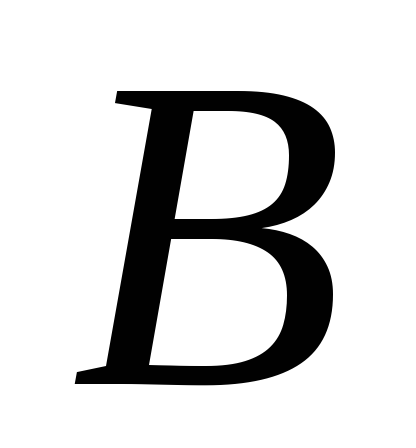• антисимметрично, так как ни для каких членов организации не выполняется одновременно « – руководитель » и «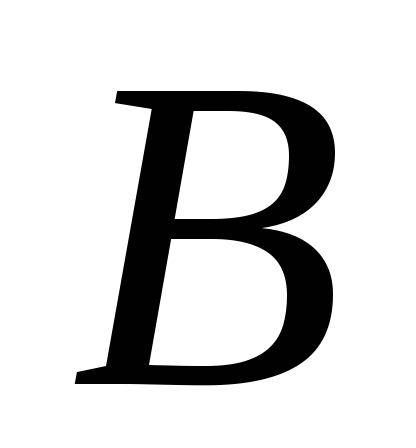 – руководитель »;

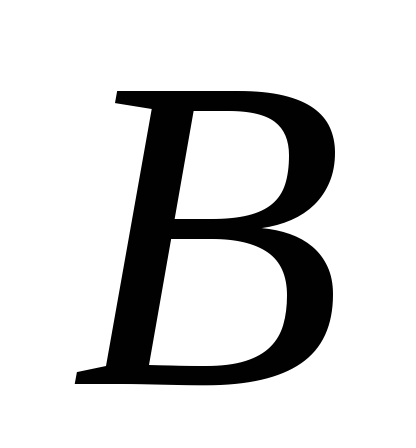• Транзитивно, так как если – руководитель и 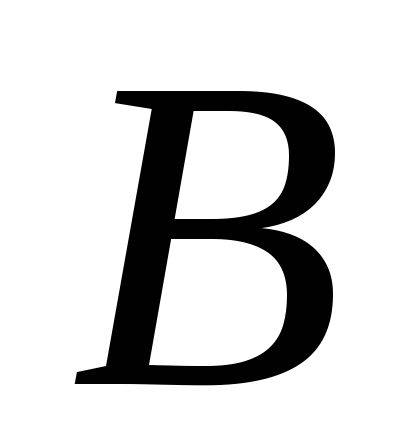– руководитель , то – руководитель .

Таким образом, отношение «быть руководителем» антирефлексивно, антисимметрично и транзитивно, т.е. является отношением строгого порядка на множестве сотрудников фирмы. Отношение задает на частичный порядок.