1.1. Множества

1.1.1. Основные определения

Фундаментальным понятием теории множеств является понятие множества. Как всякому фундаментальному понятию, ему нельзя дать четкого определения через элементарные понятия.

Под множеством интуитивно понимают совокупность определенных вполне различимых объектов, рассматриваемых как единое целое.

Отдельные объекты, из которых состоит множество, называются элементами множества.

Из определения следует, что элементы должны быть:

• вполне различимыми;

• иметь общее свойство.

Будем обозначать множества большими буквами латинского алфавита, а элементы – малыми буквами с индексами или без.

Отношение принадлежности элемента множеству обозначается

Отношение непринадлежности элемента множеству обозначается

Множество называется подмножеством множества , если всякий элемент В принадлежит . Такое отношение обозначается . Если и , то . В этом случае говорят, что есть собственное подмножество .

Примеры.

– множество студентов группы 8А03. Иванов  . Сидоров  .

– множество мужчин в группе 8А03, .

– множество студентов выше 174 см. в группе 8А83, .

Множество, состоящее из конечного числа элементов, называется конечным, в противном случае – бесконечным. Например, множество натуральных чисел , т.е. чисел 1,2,3, – бесконечно. Число элементов в конечном множестве называется его мощностью и обозначается .

Множество, не содержащее элементов, называется пустым и обозначается . Пустое множество  является подмножеством любого множества.

Если все рассматриваемые в ходе данного рассуждения множества являются подмножествами некоторого множества , то такое множество называется универсальным.

Пример. Установить истинность или ложность следующих выражений

1. .

2. .

3. .

4. .

5. .

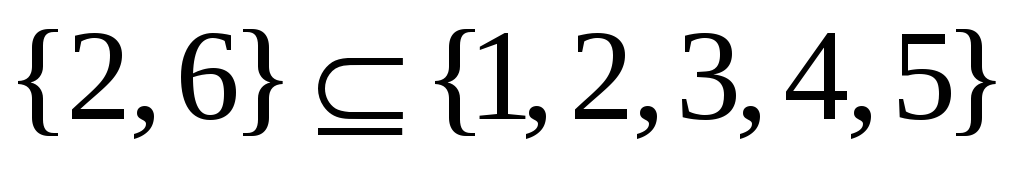Ответ. Выражения 1,3,4,5 и истинны. Выражение 2 ложно.

Пример. Справедливо ли равенство{{1,2},{2,3}}={1,2,3}?

Ответ – нет, первое множество содержит два элемента являющихся подмножествами, второе три простых элемента.

Пример. Определить мощность множеств:

Основоположником теории множеств Г. Кантором были сформулированы несколько интуитивных принципов, играющих роль аксиом. Нас интересуют два таких принципа.

Принцип объемности. Множества и считаются равными , если они состоят из одних и тех же элементов.

Чтобы сформулировать второй принцип введем понятие «формы от ». Под формой от будем понимать конечную последовательность, состоящую из слов и символа , такую, что если каждое вхождение в эту последовательность заменить одним и тем же именем некоторого предмета, то в результате получится истинное или ложное предложение. Например, формами от х являются следующие предложения: « делится на 3», «», « – валюта США». А такое предложение как «существует такое , что >0», не является формой от .

Принцип абстракции. Любая форма определяет некоторое множество , а именно множество тех и только тех предметов а, для которых – истинное предложение.

Для множества , определяемого формой , принято обозначение или . Пример:

Поскольку позволяет определить, принадлежит некоторый элемент данному множеству или нет, она иногда называется распознающей процедурой.