§ 33. Классификация картографических проекций

Применяемые для построения географических карт проекции Можно группировать по разным классификационным признакам, из Которых основными являются: а) вид «вспомогательной поверх­ности» и ее ориентировка, б) характер искажений.

Классификация картографических проекций по виду вспомога-рой поверхности и ее ориентировке. Картографические сетки получают в современном производстве аналитическим путем. |КО в названиях проекций сохранены по традиции термины 4Ндрические», «конические» и другие, соответствующие спо-Гвометрических построений, к которым в прошлом прибегали Гроения сеток. Использование при объяснении этих терми-ЮЖет уяснить особенности полученных на их основе карто-ВКИХ сеток. В настоящее время данный классификационный Трактуется как вид нормальной картографической сетки.

149

	у изонола		\
	ЛНИ

}Р

>р

--- \сж

}f

}Р

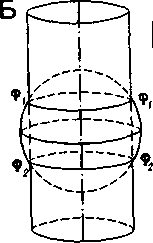
Цилиндрические проекции. При построении цилиндрических проекций представляют, что узловые точки, а значит, и линии градусной сети проектируют с шаровой поверхности глобуса на боковую поверхность цилиндра, ось которого совпадает с осью гло­буса, а диаметры обоих тел равны (рис. 140). Используя касатель­ный цилиндр в качестве вспомогательной поверхности, учитывают, что узловые точки экватора — А, В, С, D и другие одновременно находятся и на глобусе, и на цилиндре. Другие же узловые точки переносятся с глобуса на поверхность цилиндра. Так, точки Е и F, расположенные на одном меридиане с точкой С, переносятся в точ­ки Е¹ и F^x. При этом они на цилиндре расположатся на прямой, перпендикулярной линии экватора. Это и определяет форму мери­дианов в данной проекции. Параллели на поверхность цилиндра проектируются в форме окружностей, параллельных линии эква­тора (например, параллель, в которой находятся точки /*"' и g¹).

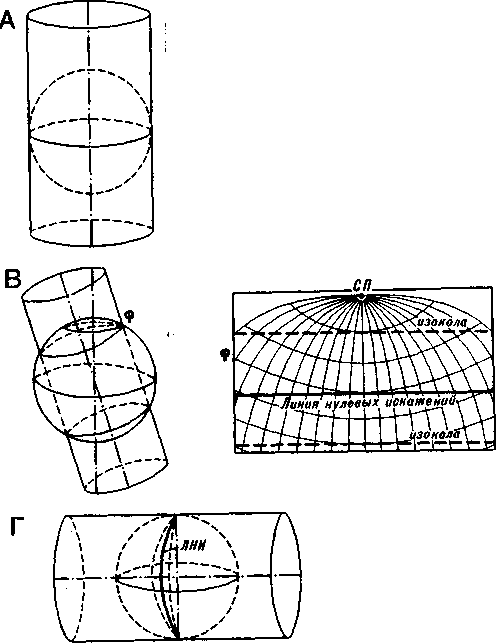
Рис. 140. Цилиндрическая проекция. Справа — развертка цилиндрической поверх­ности в плоскость с типичными для нее формами изокол

150

При развертке поверхности цилиндра в плоскость все линии картографической сетки оказываются прямыми, меридианы перпен­дикулярны параллелям и отстоят друг от друга на равных рассто­яниях. Таков общий вид картографической сетки, построенной с помощью цилиндра, касательного к глобусу и имеющего с ним общую ось.

			.
	ЛНИ
--	U30L	ола -■
	JII

₄

_I

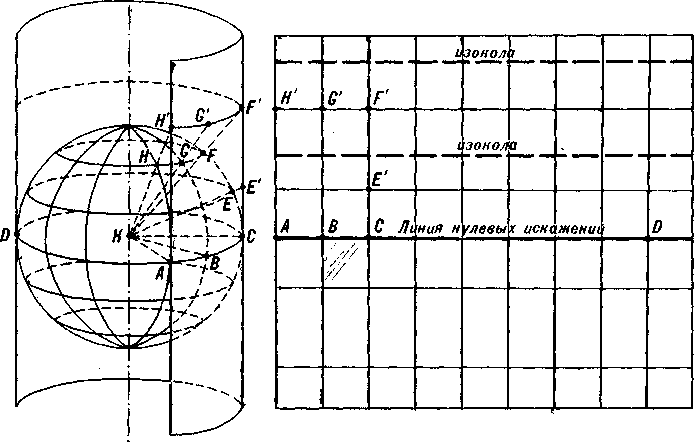
Рис 141 Варианты цилиндрических проекций: А — нормальная на касательном цилиндре; Б — нормальная на секущем цилиндре; В — косая на секущем цилиндре; Г — поперечная на касательном цилиндре; Р — область растяжения поверхности глобуса при проектировании на цилиндр; СЖ — область сжатия; ЛНИ — линия нулевых искажений

У таких цилиндрических проекций ли\нией нулевых искажений служит экватор, а изоколы имеют форму г|рямых, параллельных эк­ватору; главные направления совпадают с линиями картографичес­кой сетки, при этом с удалением от экватора искажения увеличи­ваются.

В этих проекциях применяют также проектирование на цилинд­ры с диаметром меньшим, чем диаметр глобуса, и по-разному отно­сительно глобуса расположенные (рис. 141). В зависимости от ориентировки цилиндра полученные картографические сетки (как и сами проекции) называют нормальными, косыми или поперечными. Нормальные цилиндрические сетки строят на цилиндрах, оси кото-

ГЫХ совпадают с осью глобуса (рис. 141, Л и 141,5); косые (рис. 41. в) --на цилиндрах, ось которых составляет с осью глобу-

1*51

са острый угол; поперечные сетки образуются с помощью ци­линдра, ось которого составляет прямой угол с осью глобуса (рис. 141, Г).

В каждом варианте на рисунке 141 изображен общий вид карто­ графической сетки с выделением линии нулевых искажений (ЛНИ). Нормальная цилиндрическая картографическая сетка на касатель­ ном цилиндре имеет линию нулевых искажений на экваторе. Нор­ мальная сетка на секущем цилиндре имеет две линии нулевых иска­ жений, расположенных вдоль параллелей сечения цилиндра с глобу­ сом (с широтами ф1 и фг). При этом, вследствие сжатия участка сетки между линиями нулевых искажений, масштабы длин по парал­ лелям оказываются здесь меньше главного; во внешнюю же сторо­ ну от линий нулевых искажений они больше главного масштаба — как результат растяжения параллелей при проектировании с глобуса на цилиндр. с "'

Косая цилиндрическая сетка на секущем цилиндре имеет в се­ верной части линию нулевых искажений в\форме прямой, перпен­ дикулярной к среднему меридиану карты и касательной к параллели с широтой ф; внешний вид сетки представлен кривыми линиями меридианов и параллелей. _г"~~^

Примером поперечной цилиндрической проекции может служить • проекция Гаусса-Крюгера, в которой каждый поперечно расположен-1 ный цилиндр используется для проектирования поверхности одной зоны Гаусса.

Конические проекции. Для построения картографических сеток в конических проекциях используют нормальные конусы — ка­сательный или секущий (рис. 142).

У всех нормальных конических проекций специфичен внешний вид картографической сетки: меридианы — прямые, сходящиеся в точке, изображающей на плоскости вершину конуса, параллели — дуги концентрических окружностей с центром в точке схода мери­дианов. У сеток, построенных на касательных конусах, одна линия нулевых искажений, с удалением от которой искажения увеличи­ваются (рис. 142 А). Изоколы у них имеют форму дуг окруж­ностей, совпадающих с параллелями.'Сетки, построенные на секу­щем конусе (рис. 142 Б), имеют тот же облик, но иное распределе­ние искажений: линий нулевых искажений у них две. Между ними частные масштабы вдоль параллелей меньше главного, а на внеш­них участках сетки — больше главного масштаба. Главные направле­ния у всех нормальных конических сеток совпадают с меридианами и параллелями.

Азимутальные проекции. Азимутальными называют картографи­ческие сетки, которые получают проектированием фадуснои сетки глобуса на касательную плоскость (рис. 143). Нормальную ази­мутальную сетку получают в результате переноса на плоскость, касательную к глобусу в точке полюса (рис. 143, Л), попереч­ную — при касании плоскости в точке экватора (рис. 143, Б) и ко­сую — при переносе на иначе ориентированную плоскость (рис. 143,5). Внешний вид сеток хорошо виден на рисунке.

152

f

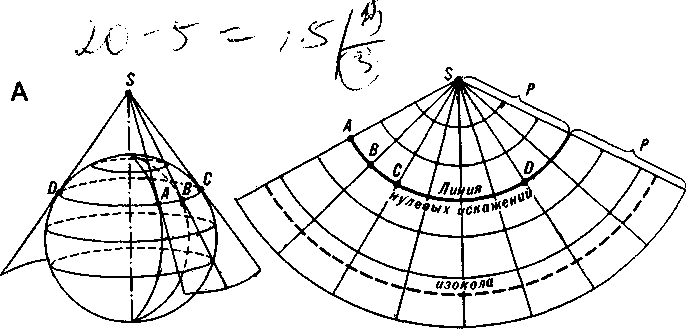
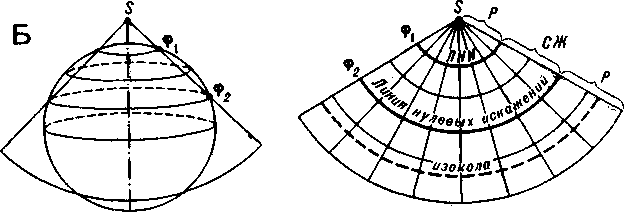
Рис 142 Распространенные варианты нормальных конических проекции: А -на касательном конусе; Б - на секущем конусе; Р - область растяжении; СЖ -область сжатия. Показана типичная форма изокол

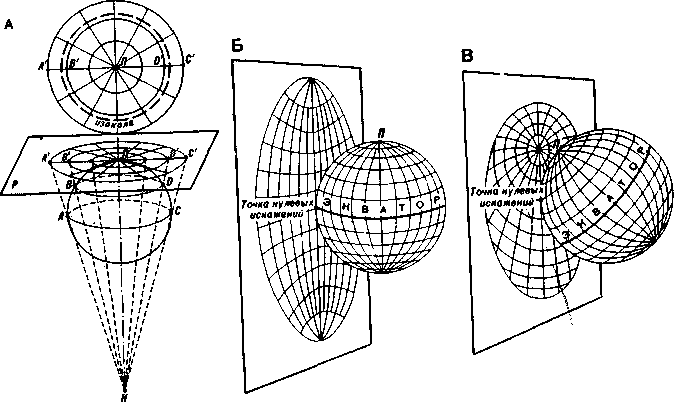
Рис. 143. Виды азимутальных проекций: А - нормальная, Б - поперечная,^ В

косая

S,

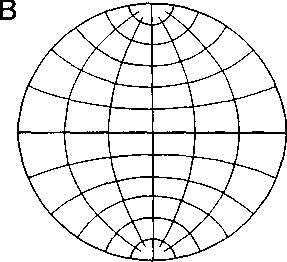Все азимутальные сетки имеют в отношении искажений следу­ющие общие свойства: точкой нулевых искажений (ТНИ) служит точка касания глобуса с плоскостью (обычно она располагайся в центре карты); величины искажений с удалением во все стороны от ТНИ возрастают, поэтому изоколы у азимутальных проекций имеют форму концентрических окружностей с центром в ТНИ

линияГ НяТ^ВЛеНИЯ ^^{еДуЮТ П}° ^РЗДИУ^СУ ^и перпендикулярным им линиям. Название этой группы проекций связано с тем, что на картографической сетке, построенной в азимутальной проекции в бывшей точке касания глобуса и плоскости (т. е. в точке нулевых искажении) азимуты всех направлений не искажаются ^У

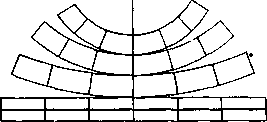
Поликонические проекции. Построение сетки в поликонической проекции можно представить путем проектирования участковгра

"Г п™ ^ГЛ°^буС-^{а На} поверхность нескольких касательных кону­сов и последующей развертки в плоскость образовавшихся на поверхности конусов полос. Общий принцип такого проектирова ния показан на рисунке 144. Буквами на рисунке 144, Л обозначе­ны вершины конусов. На каждый проектируют широтный участок поверхности глобуса, примыкающий к параллели касания соответ ствующего конуса. После развертки конусов получают изображение

Г_РяГ_м^аСТК°^{В В ВИД6 П}°^{Л0С На пл}°™и; полосе соприкасаются по среднему меридиану карты (рис. 144, Б). Окончательный вид сетка

Гн^УиТ^е(^Три^Пс^ОСЛ144^ЛИВ)^{ИАаЦИИ РЭЗРЫВОВ М6ЖДУ П}°^ЛОСаМИ "У^тем Р^астя" Для внешнего облика картографических сеток в полити­ческой проекции характерно, что меридианы имеют форму криви линии (кроме среднего - прямого), а параллели - дуги экцентр" ческих окружностей.^ поликонических проекциях используемых для построения мирокых карт, приэкваториальный участок проек­тируют на касательный цилиндр, поэтому на полученной Тетке ме^Вр^аи^Т_д°и^Ран^И_у^{МееТ Ф}°^{РМУ ПРЯМ}°^{Й ЛИНИ}М перпендикулярной среднему Картографические сетки в поликонических проекциях имеют в приэкваториальных участках масштабы длин близкие к главным ™ным^Мем^РяГ^аНГ ^{И Па}Р^алГ^ей °ни у^Деличены^И%^Иа\нит^ГЛл^аь^Вн^Но^ЬШс

CooTBercZZn⁰^ ^ЧТ° °^СОбеНН° ^{ЗЗМеТН0 В} ^Риферийных частях. Соответственно в этих частях значительно искажены и площади,

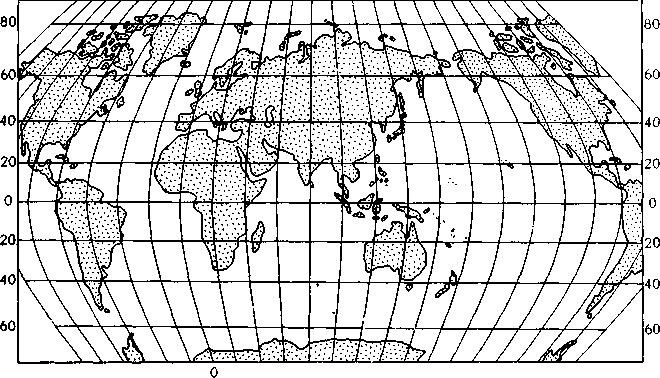
пых^У?_и°Г^Нп ^е "^{роекции}- ^К Уловным относят такие проекции, в кото­рых вид получаемых картографических сеток невозможно пред­ставить на основе проектирования на какую-нибудь вспомогатель­ную поверхность. Получают их часто аналитическим путем (на основе решения систем уравнений). Это очень большая группапроек ции^ Из них выделяют по особенностям внешнего вида картографи­ческой сетки псевдоцилиндрические проекции (рис. 145) Как вадно

лели^РИСУпоя^амь1^Пп^ея^{ВДОЦИЛИНДРИЧеСКИХ np}°^eK^ -ватор и^Кп^Вара^Нл° лели — прямые, параллельные друг другу (что полнит _Hv ^ ,„,

₌„_Ческ„_м„ проекциями), V м^дианТ fTx ™кр^.Г

154

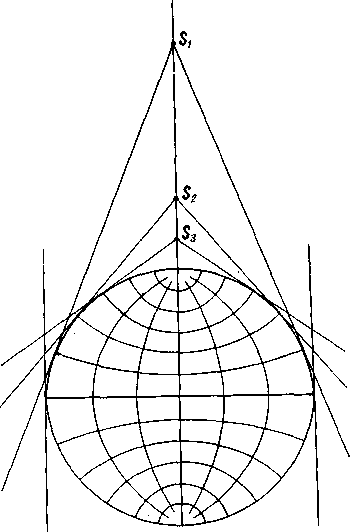
Рис. 144. Принцип построения поликонических проекций

120 80 40

40 80 120 160 160 120 80 40

160 120 80 40 0 40 80 120 160 160 120 80 40

Рис. 145. Вид картографической сетки в псевдоцилиндрической проекции

Рис. 147. Центры проектирования в нор­мальных азимутальных проекциях: К\ — центральных, Кг — стереографи­ческих, Къ — внешних, Kt — ортогра-фических

157

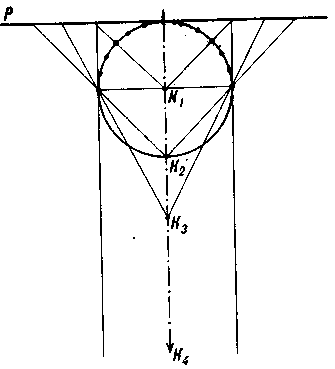
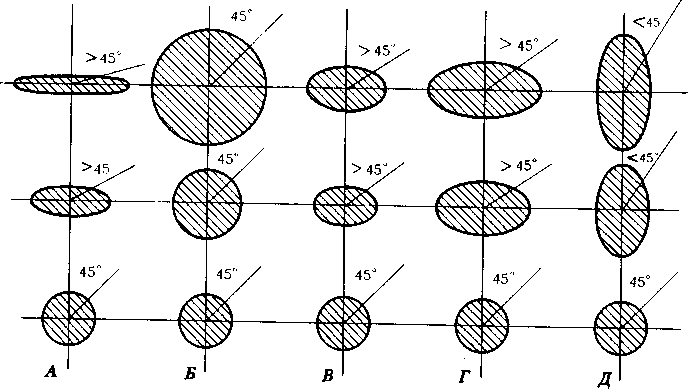
Рис. 146. Вид эллипсов искажений в проекциях равновеликих — А, равноуголь­ных — Б, произвольных — В, в том числе, равнопромежуточных по меридиану — Г и равнопромежуточных по параллели — Д. На схемах показано искажение угла

Классификация картографических проекций по характеру иска­жений. По свойствам изображенной картографической сетки проек­ции делят на равновеликие, равноугольные и произвольные.

г В равновеликих картографических проекциях масштаб площади повсюду имеет одну и ту же величину* Это свойство равновели­ких проекций можно выразить формулой:

P = ax& = Const=l. Неизбежным следствием равновеликости этих проекций являет­ся сильное искажение у них углов и форм, что хорошо поясняют эллипсы искажений (рис. 146, Л).

JB равноугольных проекциях масштабы длин в любой точке по всем направлениям одинаковы, поэтому у них нет искажения фор­мы бесконечно малых фигур и нет искажения углОЦЗ (рис. 146,5). Это общее свойство равноугольных проекций выражает формула ш = 0°. Но формы реальных (конечных) географических объектов, занимающих целые участки на карте, искажаются. У равноуголь­ных проекций наблюдаются особенно большие искажения площадей (что отчетливо демонстрируют эллипсы искажений).

* Произвольными называют картографические проекции с искаже­ниями и углов, и форм, и площадей (рис. 146, В)< Однако величина каждого вида этих искажений обычно не так велика, что у проекций двух предыдущих групп.

#Среди произвольных картографических проекций выделяют группу равнопромежуточных, у которых масштаб длин вдоль одного из главных направлений сохраняется (остается неизменным) (рис.

1 ЛИ ГМ

156