2.2. Способы задания графов

1. Список ребер (дуг) графа. В списке указываются все смежные вершины графа. Список удобно представлять в форме таблицы, в которой отмечаются парами смежные вершины. Причем, если граф ориентированный, то в каждой паре на первом месте указывается номер вершины, из которой дуга выходит, а на втором месте номер вершины, в которую дуга входит. Если в графе есть изолированные вершины, то они должны быть указаны отдельно. На рис.10 приведен список дуг графа, изображенного графически на рис.5.а)

1	1	2	2	2	4	5	5	7	7	8	8	9	9
2	4	3	4	5	8	2	6	1	8	5	9	6	8

Рис.10. Задание графа таблицей

2. Матрицы графа. Различают несколько видов матриц графа:

Матрица смежности. Если задан граф G(X,U), то ему можно поставить в соответствие квадратную матрицу смежности

, n - число вершин графа.

Общий элемент матрицы для неориентированного графа равен

где m(x_i,x_j) - кратность ребер между вершинами x_i и x_j.

Для ориентированного графа общий элемент матрицы равен

На рис. 11а приведен пример неориентированного графа и его матрица смежности, а на рис.11б ориентированного графа и его матрицы смежности. Для неориентированного графа матрица смежности симметрична относительно главной диагонали. Кроме того, сумма единиц в каждом i-том столбце или строке соответствует степени вершины x_i.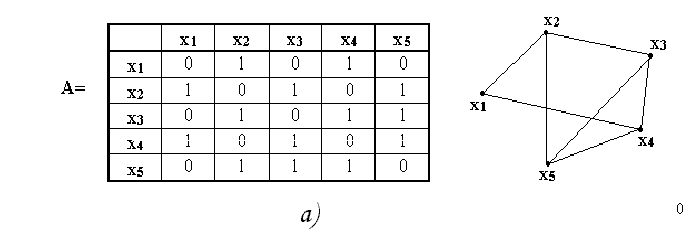

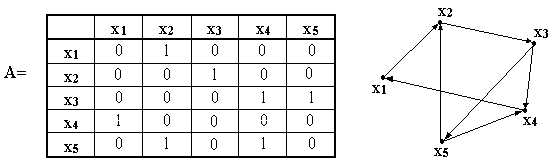
б)

Рис.11 а) Неориентированный граф и его матрица смежности;

б) Ориентированный граф и его матрица смежности.

Матрица инцидентности. Эта матрица представляет собой прямоугольную матрицу ,n - число вершин, r - число ребер (дуг). Строки матрицы соответствуют вершинам, а столбцы - ребрам (дугам) графа G(X,U).

Эта матрица может быть записана как для ориентированного графа, так и для неориентированного. Для ориентированного графа, если k-ая ветвь заходит в i-ую вершину, то на пересечении i-ой строки и k-го столбца матрицы записывается +1. Если k-ая ветвь выходит из i-ой вершины, то на пересечении k-го столбца и i-ой строки записывается -1. Правильность составления матрицы легко проверить: число единиц в i-ой строке матрицы равно степени вершины x_i графа, а число единиц в каждом столбце - двум, т.к. каждое ребро (дуга) соединяет две вершины графа.

Матрица длин. Это квадратная матрица общий элемент которой равен

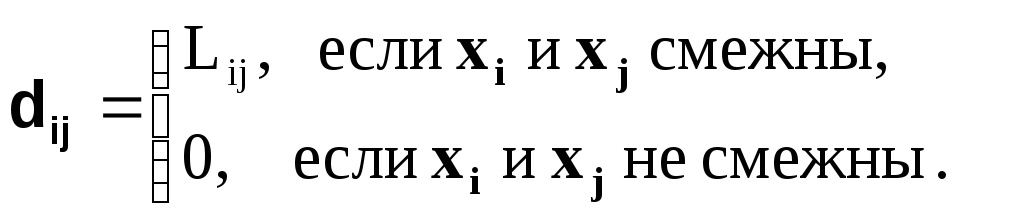
где - длина ребра (x_i, x_j).

Рис. 12. Граф и его матрица инцидентности

Над графами, также как и над множествами, можно выполнять операции объединения, пересечения, вычитания.

2.3. Операции над графами

Объединение графов. Пусть заданы два графа G₁(X₁,Г₁) и G₂(X₂,Г₂).

Объединение этих двух графов G(X,Г) определяется следующим образом:

G(X,Г)=G₁(X₁,Г₁)G₂(X₂,Г₂), при этом

X=X₁X₂, x_iX[Гx_i=Г₁x_iГ₂x_i],

т.е. отображение для каждой вершины графа G(X,Г) равно объединению отображений этой вершины для исходных графов. На рис. 13 показан пример объединения двух графов, где

X= X₁X₂ = {x₁,x₂,x₃,x₄,x₅,x₆,x₇};

Гx₁ = Г₁x₁Г₂x₁ = {x₂,x₅,x₃,x₇},

Гx₂ = Г₁x₂Г₂x₂ = {x₁,x₃,x₅} и т.д.

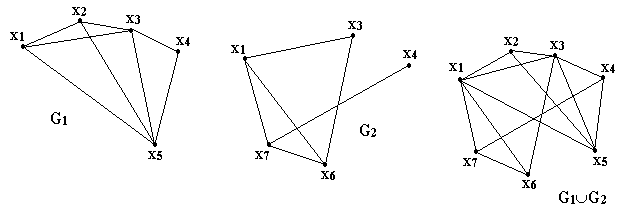
Рис. 13. Объединение графов

Пересечение графов. G(X,Г)=G₁(X₁,Г₁)G₂(X₂,Г₂). Вершинами графа G(X,Г) является пересечение вершин исходных графов: X=X₁X₂. Отображение для каждой вершины графа G(X,Г) получается в результате пересечения отображений этой вершины для исходных графов: x_iX[Гx_i=Г₁x_iГ₂x_i]. (см. рис. 14).

Рис. 14. Пересечение графов

X=X₁X₂={x₁,x₃,x₄},

Гx₁=Г₁x₁Г₂x₁={x₃} и т.д.

Вычитание графов. G(X,Г)=G₁(X₁,Г₁)\G₂(X₂,Г₂). Вершинами графа G(X,Г) является вершины графа G₁(X₁,Г₁), за исключением вершин, общих для исходных графов: X=X₁\X₂.

Отображение для каждой вершины графа G(X,Г) является пересечение множества вершин этого графа и отображения той же вершины в графе G₁(X₁,Г₁):

x_iX[Гx_i=XГ₁x_i].

В примере на рис. 15 X=X₁\X₂={x₂,x₅}; Гx₂=XГ₁x₂={x₅} и т.д.

Рис. 15. Вычитание графов