Иркутский государственный технический университет

Факультет Кибернетики

Кафедра Автоматизированных систем

Носырева Л.Л.

ДИСКРЕТНАЯ МАТЕМАТИКА

Конспективный материал к лекциям

(рабочий вариант)

Для специальностей АСУ, МЭИ, ИП, АСОК

Часть 4

Графы

Иркутск 2006

Введение.

Теория графов, как раздел дискретной математики, имеет многочисленные предметные интерпретации. Среди дисциплин и методов дискретной математики теория, графов и особенно алгоритмы на графах находят наиболее широкое примене­ние в программировании. Как показано в разделе 7.5, между понятием графа и понятием отношения, рассмотренным в главе 1, имеется глубокая связь — в сущности это равнообъемные понятия. Возникает естественный вопрос, почему же тогда графам оказывается столь явное предпочтение? Дело в том, что тео­рия графов предоставляет очень удобный язык для описания программных (да и многих других) моделей. Этот тезис можно пояснить следующей аналогией. Понятие отношения также можно полностью выразить через понятие множества (см. замечание в подразделе 1.5.1 и далее). Однако независимое определение понятия отношения удобнее — введение специальных терминов и обозначений упрощает изложение теории и делает ее более понятной. То же относится и к теории графов. Стройная система специальных терминов и обозначений тео­рии графов позволяют просто и доступно описывать сложные и тонкие вещи. Особенно важно наличие наглядной графической интерпретации понятия графа (подраздел 7.1.4). Само название «граф» подразумевает наличие графической ин­терпретации. Картинки позволяют сразу «усмотреть» суть дела на интуитивном уровне, дополняя и украшая утомительные рациональные текстовые доказатель­ства и сложные формулы.

Эта глава практически полностью посвящена описанию языка теории графов.

1. Определения графов

Как это не удивительно, но для понятия "граф" нет общепризнанного единого определения. Разные авторы, особенно применительно к разным приложениям, называют «графом» очень похожие, но все-таки различные объекты. Здесь используется терминология [26], которая была выбрана из соображений макси­мального упрощения определений и доказательств.

История теории графов

Теория графов многократно переоткрывалась разными авторами при решении различных прикладных задач.

1. Задача о Кёнuгсбергских мостах. Обойти все четыре части суши, пройдя по каждому мосту один раз, и вернуться в исходную точку (рис. 7.1). Эта задача была решена Эйлером в 1736 году.

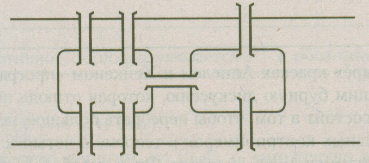
Рис. 1. Иллюстрация к задаче о Кенигсбергских мостах

2. Задача о трех домах и трех колодцах. Имеется три дома и три колодца. Про­вести от каждого дома к каждому колодцу тропинку так, чтобы тропинки не пересекались (рис. 7.2). Эта задача была решена Куратовским в 1930 году.

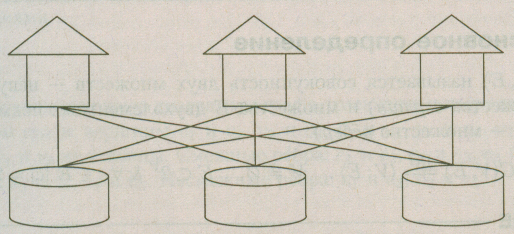
Рис.2. Иллюстрация к задаче о трех домах и трех колодцах

3. Задача о четырех красках. Любую карту на плоскости раскрасить четырьмя красками так, чтобы никакие две соседние области не были закрашены одним цветом (рис. 7.3).

Рис..3. Иллюстрация к задаче о четырех красках

Основное определение

Графом G(U, V) называется совокупность двух множеств — непустого множества U (множества вершин) и множества V бинарного отношения, определённого на множестве U.

Число вершин графа G обозначим n, а число ребер - m:

Смежность

Пусть u₁, u₂ — вершины, e = (v₂, v₁) — соединяющее их ребро. Тогда вершина u₁ и ребро е инцидентны, вершина u₂ и ребро е также инцидентны. Два ребра, инцидентные одной вершине, называются смежными; две вершины, инцидентные одному ребру, также называются смежными.

Множество вершин, смежных с вершиной u, называется множеством смежности вершины u и обозначается Г⁺(u):

ЗАМЕЧАНИЕ

Если не оговорено противное, то подразумевается Г⁺ и обозначается просто Г.

Диаграммы

Обычно граф изображают диаграммой: вершины — точками (или кружками), ребра — линиями.

Пример

На рис. 7.4 приведен пример диаграммы графа, имеющего четыре вершины и пять ребер. В этом графе вершины u₁ и u_2, u₂ и u_3, u₃ и u_4, u₄ и u_1, u₂ и u₄ смежны, а вершины u₁ и u₃ не смежны. Смежные ребра: e₁ и е₂, е₂ и е₃, е₃ и е₄, е₄ и e₁, e₁ и е₅, е₂ и е₅, е₃ и е₅, е₄ и е₅. Несмежные ребра: e₁ и е₃, е₂ и е₄.

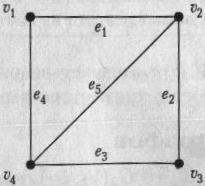
Рис.4. Диаграмма графа

Виды графов

1. Если элементами множества Е являются упорядоченные пары, то граф назы­ вается ориентированным (или орграфом). В этом случае элементы множества V называются узлами, а элементы множества Е — дугами.

2. Если элементом множества Е может быть пара одинаковых (не различных) элементов V, то такой элемент множества Е называется петлей, а граф называется графом с петлями (или псевдографом).

3. Если Е является не множеством, а набором, содержащим несколько одинаковых элементов, то эти элементы называются кратными ребрами, а граф назы­вается мулътшрафом.

4. Если элементами множества Е являются не обязательно двухэлементные, а любые подмножества множества V, то такие элементы множества Е называются гипердугами, а граф называется гиперграфом.

5.Если задана функция F: V→М и/или F: Е→М, то множество М называется множеством пометок, а граф называется помеченным (или нагруженным). В качестве множества пометок обычно используются буквы или целые числа.

Изоморфизм графов

Говорят, что два графа G₁(V₁,E₁) и G₂(V₂,E₂) изоморфны (обозначается G₁ ~ G₂), если существует биекция h: V₁ → V₂, сохраняющая смежность:

e₁ = (u,v) ∊ Е₁<=>e₂ = (h(u),h(v)) ∊ E₂,

Изоморфизм графов есть отношение эквивалентности. Действительно, изомор­физм обладает всеми необходимыми свойствами:

рефлексивность: G ~ G, где требуемая биекция суть тождественная функция;

симметричность: если G₁ ~ G₂ с биекцией h, то G₂ ~ G₁ с биекцией h^-1;

транзитивность: если g₁ ~ G₂ с биекцией h и G₂ ~ G₃ с биекцией g, то g₁ ~ G₃ с биекцией g∙h.

Графы рассматриваются с точностью до изоморфизма, то есть рассматриваются классы эквивалентности по отношению изоморфизма (см. раздел 2.2).

Элементы графов

После рассмотрения определений, относящихся к графам как к цельным объек­там, естественно дать определения различным составным элементам графов.

Подграфы

Граф G'(V’, E') называется подграфом графа G(V, E) (обозначается G’ G), если V’ V и/или Е'  Е.

Если V’ = V, то G' называется остовным подграфом G.

Если V’ V &Е'  E&(V’≠ V  Е' ≠ Е), то граф G' называется собственным подграфом графа G.

Подграф G'(V',E'} называется правильным подграфом графа G(V,E), если G' содержит все возможные ребра G:

u,v∊V’ (u,v) ∊ E(u,v) ∊E'.

Правильный подграф G'(V’, E') графа G(V, E) определяется подмножеством вер­шин V’.

Валентность

Количество ребер, инцидентных вершине v, называется степенью (или валент­ностью) вершины v и обозначается d(v):

 ∊ V0≤d()≤p - l, d() = Г⁺().

Обозначим минимальную степень вершины графа G через δ(G), а максималь­ную — через ∆(G):

Если степени всех вершин равны k, то граф называется регулярным степени k:

δ(G) = (G) = k.

Степень регулярности является инвариантом графа и обозначается r(G). Для нерегулярных графов r(G) не определено.

Пример

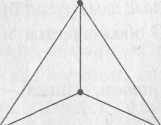
Рис. 7.7. Диаграмма регулярного графа степени 3

Если степень вершины равна 0 (то есть d(v) = 0), то вершина называется изолиро­ванной. Если степень вершины равна 1 (то есть d(v) = 1), то вершина называется концевой, или висячей.

Для орграфа число дуг, исходящих из вершины v, называется полустепенъю исхо­да, а входящих — полустепенью захода. Обозначаются эти числа, соответственно, d^-(v) и d⁺(v).

ТЕОРЕМА (Эйлера) Сумма степеней вершин графа равна удвоенному количеству ребер:

= 2q.

доказательство

При подсчете суммы степеней вершин каждое ребро учитывается два раза: для одного конца ребра и для другого. 

Маршруты, цепи, циклы

Маршрутом в графе называется чередующаяся последовательность вершин и ребер v₀,e₁,v₁,e₂,v₂,...,e_k,v_k, в которой любые два соседних элемента инцидентны.

ЗАМЕЧАНИЕ

Это определение подходит также для псевдо-, мульти- и орграфов. Для «обычного» графа достаточно указать только последовательность вершин или только последовательность ребер.

Если ₀ = _k, то маршрут замкнут, иначе открыт.

Если все ребра различны, то маршрут называется цепью. Если все вершины (а значит, и ребра) различны, то маршрут называется простой цепью. В цепи ₀,e_l,... ,e_k,_k вершины v₀ и v_k называются концами цепи. Говорят, что цепь с концами и и v соединяет вершины и и v. Цепь, соединяющая вершины и и v, обозначается (и, v). Очевиднб, что если есть цепь, соединяющая вершины и и v, то есть и простая цепь, соединяющая эти вершины.

Замкнутая цепь называется циклом; замкнутая простая цепь называется простым циклом. Число циклов в графе G обозначается z(G). Граф без циклов называется ациклическим.

Для орграфов цепь называется путем, а цикл — контуром.

Пример

В графе, диаграмма которого приведена на рис. 7.8:

1.₁, ₃, ₁, ₄ — маршрут, но не цепь;

2. _1, _3, _5, _2, _3, ₄ — цепь, но не простая цепь;

3. _1, _4, _3, _2, ₅ — простая цепь;

4. _1, _3, _5, _2, _3, _4, ₁ — цикл, но не простой цикл;

5. _1, _3, _4, ₁ — простой цикл.

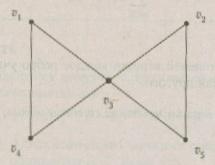
Рис.8. Маршруты, цепи, циклы

Расстояние между вершинами

Длиной маршрута называется количество ребер в нем (с повторениями). Если маршрут М= v₀, e₁,₁,e₂,v₂,..., e_k, _k то длина М равна k (обозначается |М| = k).

Расстоянием между вершинами и и v (обозначается d(u,v)) называется длина кратчайшей цепи (u,v), а сама кратчайшая цепь называется геодезической.

ЗАМЕЧАНИЕ -

Если  и, v, то по определению d(u, v).

Диаметром графа G (обозначается D(G)) называется длина длиннейшей геоде­зической.

Множество вершин, находящихся на одинаковом расстоянии n от вершины v (обозначение D(v,n)), называется ярусом:

D(v,u).

Связность

Говорят, что две вершины в графе связаны, если существует соединяющая их (простая) цепь. Граф, в котором все вершины связаны, называется связным.

Отношение связанности вершин является эквивалентностью. Классы эквива­лентности по отношению связанности называются компонентами связности гра­фа. Число компонент связности графа G обозначается k(G). Граф G является связным тогда и только тогда, когда k(G) = 1. Если k(G) > 1, то G — несвязный граф. Граф, состоящий только из изолированных вершин (в котором k(G) = p(G) и r(G) = 0), называется вполне несвязным.

Виды графов и операции над графами

В данном разделе рассматриваются различные частные случаи графов и вводят­ся операции над графами и их элементами. Заметим, что не все из используемых обозначений операций над графами являются традиционными и общепринятыми.

Тривиальные и полные графы

Граф, состоящий из одной вершины, называется тривиальным. Граф, состоящий из простого цикла с k вершинами, обозначается С_k.

Пример

С₃ — треугольник.

Граф, в котором каждая пара вершин смежна, называется полным. Полный граф с р вершинами обозначается К_р, он имеет максимально возможное число ребер:

Полный подграф (некоторого графа) называется кликой (этого графа).

Двудольные графы

Двудольный граф (или биграф, пли четный граф) — это граф G(V,E), такой что множество V разбито на два непересекающихся множества V₁ и V₂ (V₁  V₂ = V & V₁  V₂ = ), причем всякое ребро из Е инцидентно вершине из V₁ и вершине из V₂ (то есть соединяет вершину из V₁ с вершиной из |V₂). Множества V₁ и V₂ называются долями двудольного графа. Если двудольный граф содержит все ребра, соединяющие множества V₁ и V₂, то он называется полным двудольным графом. Если |V₁| = m и |V₂| = п, то полный двудольный граф обозначается K_m,n.

Пример

На рис. 7.9 приведена диаграмма графа К₃,₃.

Рис..9. Диаграмма графа Кз,з

ТЕОРЕМА Граф является двудольным тогда и только тогда, когда все его про­стые циклы, имеют четную длину.

доказательство

[Необходимость.] От противного.

Пусть G(V₁,V₂;E) — двудольный граф, и _1, ₂,..., _2k+1, ₁ — простой цикл не­четной длины. Пусть ₁ ∊ V₁, тогда ₂ ∊ V₂, ₃ ∊ V₁, ₄ ∊ V₂,... , _2k+1 ∊ V₁. Имеем: _1, _2k+1 ∊ V₁ и (_1, _2k+1)∊ E, что противоречит двудольности.

[Достаточность.] Не ограничивая общности, можно считать, что G — связный граф, поскольку каждую компоненту связности можно рассматривать отдельно. Разо­бьем множество V на V₁ и V₂ с помощью следующей процедуры:

Вход: граф G(V,E).

Выход: Множества V₁ и V₂ — доли графа.

select  ∊ V { произвольная вершина }

V₁: =  { в начале первая доля содержит , ... }

V₂ : =  { ... а вторая пуста }

for и ∊ V \ {} do

if d(, u] — четно then

V₁: = V₁ + u { помещаем вервину u в первую долю }

else

V₂ : = V₂ +u {помещаем вершину u во вторую долю }

end if

end for

Далее от противного. Пусть есть две вершины в одной доле, соединенные ребром. Пусть для определенности u, ω ∊ V₂ и (u, ω) ∊ Е.

Рассмотрим геодезические , u и , ω (здесь  — та произвольная вершина, ко­торая использовалась в алгоритме построения долей графа). Тогда длины | , u| и | , ω | нечетны. Эти геодезические имеют общие вершины (по крайней мере, вершину ). Рассмотрим наиболее удаленную от  общую вершину геодезиче­ских , u и , ω и обозначим ее ' (может оказаться так, что  = '). Имеем: | ’, u| + | ’, ω | = | , u| + | , ω -2| , ’| -четно, и ',...,u,ω,...,' -простой цикл нечетной длины, что противоречит условию. Если же , ω ∊ V₁, то длины | , u| и | , ω | четны и аналогично имеем: ',...,u,ω,...,' — простой цикл нечетной длины.

Направленные орграфы и сети

Если в графе ориентировать все ребра, то получится орграф, который называется направленным. Направленный орграф, полученный из полного графа, называется турниром.

ОТСТУПЛЕНИЕ---------------------------------------------------------------------------------------------------------------

Название «турнир» имеет следующее происхождение. Рассмотрим спортивное соревно­вание для пар участников (или пар команд), где не предусматриваются ничьи. Пометим вершины орграфа участниками и проведем дуги от победителей к побежденным. В таком случае турнир в смысле теории графов — это как раз результат однокругового турнира в спортивном смысле.

--------------------------------------------------------------------------------------------------------------------------------------

Если в орграфе полустепень захода некоторой вершины равна нулю (то есть d⁺() = 0), то такая вершина называется источником, если же нулю равна полу­степень исхода (то есть d^-() = 0), то вершина называется стоком. Направлен­ный орграф с одним источником и одним стоком называется сетью.

Операции над графами

Введем следующие операции над графами:

1. Дополнением графа G(V₁,E₁) (обозначение — (V₁,E₁)) называется граф G(V₂,E₂), где V₂= V₁& E₂=

2. Объединением графов G₁(V₁,E₁) и G₂(V₂,E₂) (обозначение - G₁(V₁,E₁)G₂(V₂,E₂), при условии V₁  V₂ = , E₁ E₂ = ) называется граф G(V,E), где C.

Пример

= С₃  С₃.

3. Соединением графов G₁(V₁,E₁) и G₂(V₂,E₂)

(обозначение – G₁(V₁,E₁) + G₂(V₂, Е₂), при условии V₁V₂= , E₁ E₂ =  называется граф G(V,E), где

V = V₁V₂&E= E₁ E_2{e= (_1, ₂)| ₁∊V_l&₂∊V₂}.

Пример

= + .

4. Если V₁V₂, то пересечением G₁G₂ графов G₁ и G₂ называется граф (V₁V₂, E₁E₂).

5. Кольцевой суммой G₁  G₂ называется граф (V₁V₂,E₁E₂), где E₁E₂= (E₁\E₂)(E₂\E₂)

Пример

Для графов G₁({a₁, a₂, a₃},{[ a₁, a₂],( a₂, a₃)}) и G₂({a₁, a₂, a₄},{( a₁, a₂₎,( a₄, a₁)}) (рис. 4.12) найдём G₁G₂, G1G2, G₁G₂. По определению имеем G₁G₂=({a₁, a₂, a₃},{[ a₁, a₂],( a₂, a₃), ( a₄, a₁)}), G1G2=({a₁, a₂},{( a₁, a₂)}), G₁G₂==({a₁, a₂, a₃, a₄},{( a₂, a₁),( a₂, a₃) ,( a₄, a₁)}).

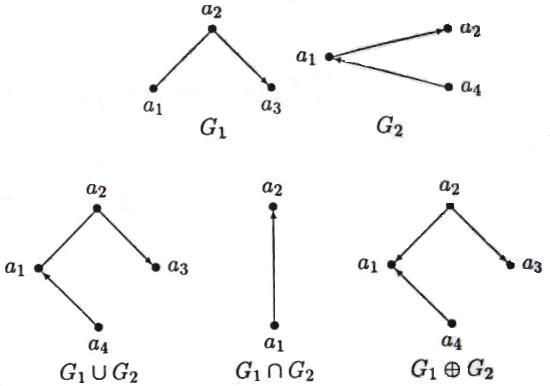
Рис. 4.12

6. Произведением G₁G₂ графов G₁ и G₂ называется граф, (V₁V₂,E), в котором ((a₁, b₁),( a₂, b₂))∊R тогда и только тогда, когда a₁= a₂ и (b₁, b₂)∊R₂ , или b₁= b₂ и (a₁, a₂)∊R₁.

Пример

На рис. 4.14 изображено произведение G₁G₂ графов G₁=({1,2},{(1,1),(2,1)}) и G₂=({a,b,c},{[a,b],(b,c)}).

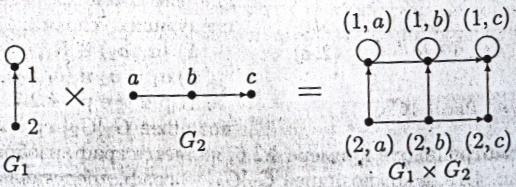
Рис. 4.14

7. Удаление вершины v из графа G₁(V₁,E₁) (обозначение — G₁(V₁,E₁) - v, при условии v ∊ V₁) дает граф G₂(V₂,E₂), где V₂ = V₁\{v}&E₂= E₁\{e = (v₁,v₂) | v₁ = v  v₁ = v} .

Пример

C₃-v = K₂.

8. Удаление ребра е из графа G₁(V₁,E₁) (обозначение — G₁(V₁,E₁) - e, при усло­вии е ∊ E₁) дает граф G₂(V₂, E₂), где V₂=V₁&E₂=E₁\{e}.

Пример

К₂-e = .

9.Добавление вершины v в граф G₁(V₁,E₁) (обозначение — G₁(V₁,E₁) + v, при условии v ∊ V₁) дает граф G₂(V₂,E₂), где V₂=V₁{v}&E₂=E₁.

Пример

K₂ + v = K₂  K₁.

10. Добавление ребра е в граф G₁(V₁,E₁) (обозначение — G₁(V₁,E₁) + е, при усло­вии е ∊ E₁) дает граф G₂(V₂, E₂), где V₂=V₁&E₂=E₁{e}.

11. Стягивание подграфа А графа G₁(V₁,E₁) (обозначение — G₁(V₁,E₁) /A, при условии А  V₁, v∊V₁) дает граф G₂(V₂,E₂), где V₂=(V₁\A){v}&

E₂=E₁\{e=(u,w)|u∊Aw∊A}{e=(u,v)|u∊Г(A)\A}.

Пример

K₄/C₃=K₂.

12. Размножение вершины v графа G₁(V₁,E₁) (обозначение — G₁(V₁,E₁)↑v при условии v∊V₁, v’V₁) дает граф G₂(V₂, E₂), гдеV₂ : = V₁  {v’} & E₂ : = E₁{(v, v')}{е = (u,v')|u∊ Г⁺(v) } .

Пример K₂↑v=C₃.

13. Операция отождествления вершин v и u графа G(V,E) состоит в удалении из графа G вершин v и u и присоединении новой вершины v’, дуг (v’,c), если (v, c)∊E или (u,c)∊E, и дуг (c,v’), если (c,v)∊E или (c, u)∊E: (V\{v,u}){v’},(E\{(c,d)|c=v или d=v, или c=u, или d=u}){(v’,c)|(v,c)∊E, или (u,c)∊E}{(c,v’)|(c,a)∊E, или (c,u)∊E}.

Говорят, что построенный граф получается из графа G отождествлением вершин v и u. В случае, когда v и u соединены дугой, операцию отождествления вершин v и u называют стягиванием дуги (v,u).

Пример

Из графа G, показанного на рис. 4.10, добавлением вершины 5 образуется граф G₁, добавлением дуги (3,1) – граф G₂, удалением дуги (3,2) – граф G₃, удалением вершины 2 – граф G₄, отождествлением вершин 1 и 4 – граф G₅, стягиванием дуги (2,3) – граф G₆.

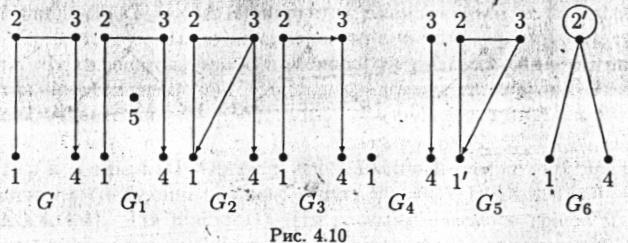
Рис. 4.10.

Представление графов в ЭВМ

Следует еще раз подчеркнуть, что конструирование структур данных для пред­ставления в программе объектов математической модели — это основа искус­ства практического программирования. Мы приводим четыре различных базовых представления графов. Выбор наилучшего представления определяется требова­ниями конкретной задачи. Более того, при решении конкретных задач исполь­зуются, как правило, некоторые комбинации или модификации указанных пред­ставлений, общее число которых необозримо. Но все они так или иначе основаны на тех базовых идеях, которые описаны в этом разделе.

Требования к представлению графов

Известны различные способы представления графов в памяти компьютера, кото­рые различаются объемом занимаемой памяти и скоростью выполнения опера­ций над графами. Представление выбирается, исходя из потребностей конкрет­ной задачи. Далее приведены четыре наиболее часто используемых представле­ния с указанием характеристики n(р, q) — объема памяти для каждого предста­вления. Здесь р — число вершин, a q — число ребер.

ЗАМЕЧАНИЕ

Указанные представления пригодны для графов и орграфов, а после некоторой модифи­кации также и для псевдографов, мультиграфов и гиперграфов.

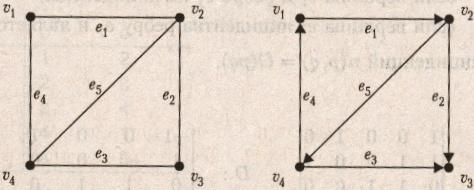
Рис.10 Диаграммы графа (слева) и орграфа (справа), используемых в качестве примеров

Представления иллюстрируются на конкретных примерах графа G и орграфа D, диаграммы которых представлены на рис. 7.10.

Матрица смежности

Представление графа с помощью квадратной булевской матрицы

М : array [l..p,l..p] of 0..1,

отражающей смежность вершин, называется матрицей смежности, где

Для матрицы смежности n(p,q) = О(р²).

Пример

Матрица инциденций

Представление графа с помощью матрицы H : array [l..p, l..q] of 0..1 (для оргра­фов H : array [l..p, l..g] of —1..1), отражающей инцидентность вершин и ребер, называется матрицей инциденций, где для неориентированного графа

а для ориентированного графа

Для матрицы инциденций n(p,q) = O(pq).

Пример

. Списки смежности

Представление графа с помощью списочной структуры, отражающей смежность вершин и состоящей из массива указателей Г : array [l..p] of ↑ N на списки смеж­ных вершин (элемент списка представлен структурой N : record v : l..p; n :↑ N end record), называется списком смежности. В случае представления неориенти­рованных графов списками смежности n(p,q) = O(p+2q), а в случае ориентиро­ванных графов n(р, q) = О(р + q).

Пример

Списки смежности для графа G и орграфа D представлены на рис.7.11.

Рис. 7.11. Списки смежности для графа G (слева) и орграфа D (справа)