
- •Министерство образования и науки Украины
- •Введение
- •1. Элементы теории множеств
- •1.1. Основные определения
- •Операции над множествами
- •1.3. Упорядоченное множество и прямое произведение множеств
- •1.4. Соответствия
- •1.5. Конечные и бесконечные множества. Мощность множества
- •2. Элементы теории графов
- •2.1. Основные определения
- •2.2. Способы задания графов
- •2.3. Операции над графами
- •2.4. Характеристические числа графов
- •2.5. Плоские графы
- •3. Элементы математической логики
- •3.1. Элементарные логические функции
- •3.2. Принцип суперпозиции. Законы и тождества алгебры логики
- •3.3. Способы задания логической функции
- •3.4. Конституенты единицы и нуля. Составление логической формулы по
- •3.5. Полином Жегалкина
- •3.6. Замкнутые классы логических функций
- •Элементарных булевых функций
- •Дизъюнктивные и конъюнктивные нормальные формы булевых функций
- •Минимизация булевых функций
- •1. Заданная функция преобразуется в сднф.
- •Минимизация не полностью определенных булевых функций
- •Синтез схем со многими выходами
- •4. Конечные автоматы
- •Основные понятия и определения
- •Переход от автомата Мили к эквивалентному автомату Мура и наоборот
- •Минимизация числа состояний конечного автомата
- •Постановка задачи синтеза автоматов
- •Структурно полные системы автоматов. Теорема о структурной полноте
- •Элементарные автоматы
- •4. 4. 3. Структурный синтез конечных автоматов
- •5. Случайные процессы в системах управления
- •5.1. Случайные величины и их основные характеристики
- •5.1.1. Интегральный закон распределения (функция распределения)
- •5.1.2. Дифференциальный закон распределения (плотность вероятности)
- •5.1.3. Моменты случайных величин и их свойства
- •5.2. Векторные случайные величины
- •5.2.1. Функция распределения двумерного случайного вектора
- •5.2.2. Функция плотности вероятности двумерного случайного вектора
- •5.2.3. Моменты системы случайных величин
- •5.3. Случайные функции. Многомерные законы распределения
- •5.4. Характеристики случайных функций
- •5.5. Операции над случайными функциями
- •5.5.1. Суммирование случайной и детерминированной функций
- •5.5.2. Интегрирование случайной функции
- •5.5.3. Дифференцирование случайной функции
- •5.5.4. Сложение случайных функций
- •5.6. Стационарные случайные процессы
- •5.6.1. Эргодическая теорема
- •5.6.2. Корреляционная функция стационарного случайного процесса
- •5.6.3. Расчет корреляционной функции по экспериментальным данным
- •5.7. Спектральная плотность стационарного случайного процесса
- •5.8. Связь между спектральной плотностью и корреляционной функцией стационарного случайного процесса
- •5.9. Случайные функции и их характеристики (примеры)
- •5.10. Прохождение стационарного случайного сигнала через линейную систему
3.2. Принцип суперпозиции. Законы и тождества алгебры логики
Выражения, построенные из конечного числа логических переменных, знаков логических функций, а также констант 0 и 1 называют булевыми формулами. Каждая булева формула может рассматриваться как некоторая булева функция от логических переменных, значение которой на каждом наборе переменных можно получить, если подставить значения переменных (0 или 1) на этом наборе в формулу и произвести указанные логические операции.
В логическую формулу вместо любой ее буквы можно подставить как независимую переменную, так и переменную, являющуюся функцией других переменных. В этом заключается принцип суперпозиции, т.е. подстановки булевых функций вместо аргументов в другую булеву функцию. С помощью принципа суперпозиции любая булева функция может быть представлена как некоторая комбинация функций двух переменных, полный набор которых представлен в табл.2.
Могут быть построены различные логические функции A(X,Y,Z,...) и B(X,Y,Z,...) от одних и тех же логических переменных X,Y,Z,... которые имеют одни и те же значения на всех одинаковых наборах переменных, т.е. A(X,Y,Z,...) = B(X,Y,Z,...)
Такое соотношение называется логическим тождеством. Для проверки тождества можно строить таблицы истинности для левой и для правой частей и сравнивать значения функций на всех наборах переменных.
Например,
рассмотрим тождество (XY)
+
![]() Y
=
Y
=
![]() + Y . Построим
таблицу истинности для левой и для
правой частей выражения и сравним их
значения на всех наборах переменных X
и Y
(табл.3). Из таблицы видно, что это
выражение представляет собой тождество.
+ Y . Построим
таблицу истинности для левой и для
правой частей выражения и сравним их
значения на всех наборах переменных X
и Y
(табл.3). Из таблицы видно, что это
выражение представляет собой тождество.
Таблица 3
-
X
Y
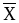
XY
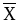 Y
Y(XY)+
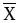 Y
Y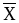 +Y
+Y0
0
1
1
0
1
1
1
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
0
1
0
1
1
Рассмотрим важнейшие тождества алгебры логики.
-
X X = X,
X + X = X,
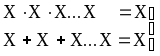
Законы идемпотентности.
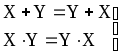
Коммутативные законы.
-
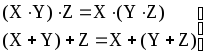
Ассоциативные законы.
-
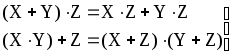
Дистрибутивные законы.
X + 1 = 1, X + 0 = X
X 1 = X, X 0 = 0.
X
+
![]() =
1. Закон
исключенного третьего.
=
1. Закон
исключенного третьего.
X
![]() = 0. Закон
противоречия.
= 0. Закон
противоречия.
-
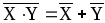 ,
,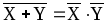 .
.Законы де Моргана.
![]() . Закон
двойного отрицания.
. Закон
двойного отрицания.
Рассмотрим еще несколько тождеств, в которых логические выражения, содержащие различные функции, приравниваются к выражениям, содержащим лишь функции отрицания, конъюнкции и дизъюнкции.
X
Y =![]() Y
+ X
Y
+ X![]() .
.
X
Y
=
![]() + Y.
+ Y.
X
Y = XY
+
![]()
![]() .
.
Если некоторая логическая функция тождественно равна единице, то она называется тавтологией. Если нулю - противоречием.
3.3. Способы задания логической функции
Существует ряд способов задания логической функции. Рассмотрим важнейшие из них.
1.
Формула,
указывающая последовательность
логических операций, которые нужно
произвести над высказываниями -
аргументами, чтобы получить значение
функции. Например,
F(X1,
X2,
X3)
= X1![]() X3.
X3.
2. Таблица истинности. В таблице указываются значения функции в зависимости от значений истинности аргументов. Если функция зависит от n аргументов, то число всех наборов аргументов равно 2n.
В таблице истинности указываются все наборы и значение функции на каждом наборе.
3. Числовой способ задания функции. Каждой независимой переменной-аргументу функции ставится в соответствие число 2k (k = 0, 1, 2,...). Аргументы функции записываются в виде упорядоченного множества, например, F(X1, X2, X3). При этом переменная, записанная крайней справа, получает коэффициент 20 = 1, переменная, стоящая рядом слева, получает коэффициент 21=2 и т. д. Так, для функции F(X1, X2, X3) независимые переменные получают следующие коэффициенты: X3-1, X2-2. X1-4. Для каждого набора независимых переменных определяется число номер N по формуле
N = 4 X1 + 2 X2 + 1 X3
При задании функции указывают номера тех наборов, на которых функция равна единице, и перед списком номеров единичных наборов ставят знак дизъюнкции. Можно также указать те номера наборов, на которых функция равна нулю, но при этом перед списком нулевых наборов ставят знак конъюнкции. Например, функция, заданная таблицей истинности (табл.4) может быть записана следующим образом: F(X,Y,Z) = (0,1,4,7) = (2,3,5,6)
логической
функции
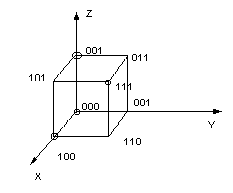 Рис.18.
Геометрический способ задания
Рис.18.
Геометрический способ задания
|
N |
X |
Y |
Z |
F |
|
0 |
0 |
0 |
0 |
1 |
|
1 |
0 |
0 |
1 |
1 |
|
2 |
0 |
1 |
0 |
0 |
|
3 |
0 |
1 |
1 |
0 |
|
4 |
1 |
0 |
0 |
1 |
|
5 |
1 |
0 |
1 |
0 |
|
6 |
1 |
1 |
0 |
0 |
|
7 |
1 |
1 |
1 |
1 |
4. Геометрический способ задания логической функции. Для функции n - независимых логических переменных рассматривается единичный n- мерный куб. Вершины куба соответствуют наборам независимых переменных. Каждой вершине приписывают значение функции на соответствующем наборе. На рисунке единичные наборы помечают, например, кружками. (рис.18).
5. Логическая схема, представляющая собой условное графическое обозначение логических функций. На рис.19 показаны графические обозначения некоторых элементарных логических функций. На рис.20 показан пример логической схемы.
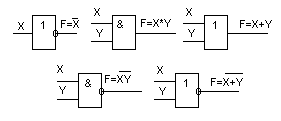
Рис.19. Графические обозначения элементарных логических функций.
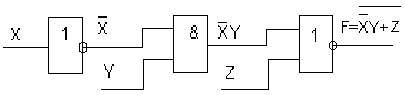
Рис.20. Логическая схема.
