2. Операции над множествами

Объединение множеств . Объединением множеств X и Y называется множество, состоящее из всех тех и только тех элементов, которые принадлежат X или принадлежат Y. Объединение обозначается через XY. Суть операции легко понять, пользуясь диаграммами Эйлера-Венна. Пусть X-множество точек левого круга (Рис.1а), Y-множество точек правого круга. Тогда XY - заштрихованная область.

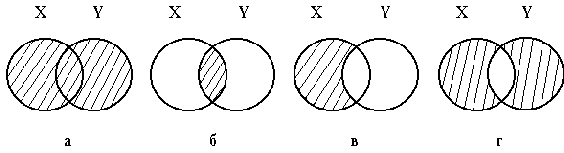
Рис.1. Диаграммы Эйлера-Венна

Пересечение множеств. Пересечением множеств X и Y называется множество, состоящее из всех тех и только тех элементов, которые принадлежат как множеству X, так и множеству Y. Пересечение множеств обозначается через XY. На рис.1б пересечение множеств X и Y соответствует заштрихованной области. Если XY=, то множество X и Y называются непересекающимися.

Разность множеств. Разностью множеств X и Y называется множество, состоящее из тех и только тех элементов, которые принадлежат X и не принадлежат Y. Обозначается разность множеств следующим образом: X\Y . На рис1.в заштрихована область, соответствующая разности множеств X и Y.

Симметрическая разность множеств. Симметрической разностью множеств X и Y называется множество, состоящее из всех тех и только тех элементов, которые принадлежат или множеству X, или множеству Y, но не обоим вместе. Обозначается симметрическая разность множеств следующим образом: XY.На рис1.г заштрихованная область соответствует XY.

Дополнение множества. Множество , определяемое из соотношения =J\X называется дополнением множества X. Пусть множество точек прямоугольника на рис.2 составляет универсальное множество J, X-множество точек круга. Тогда - множество точек заштрихованной области. Множества X и не имеют общих элементов, поэтому X=. Кроме того не имеется элементов в множестве J, которые не принадлежали бы ни X, ни , т.к. те элементы, которые не принадлежатX принадлежат . СледовательноX= J.

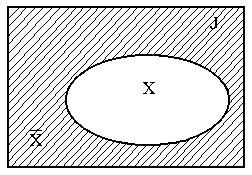
Рис.2. - дополнение множестваX

Разбиение множества. Некоторые множества можно представить как систему подмножеств. Так, например, множество студентов института составляют систему подмножеств факультетов, либо систему подмножеств курсов.

Рассмотрим некоторое множество М и систему множеств S={X₁, X₂,...,X_n}. Система множеств S называется разбиением множества M, если она удовлетворяет следующим условиям.

1. Любое множество X_i (i=1,2,...,n) из S является подмножеством множества M - X_i M, т.е. XS: XM.

2. Любые два множества X_i и X_j из S являются непересекающимися - X_iX_j=, если ij, т.е. X_iS и X_jS (ij): X_iX_j=.

3. Объединение всех множеств, входящих в разбиение, равно множеству M–

.

Тождества алгебры множеств. С помощью различных операций над множествами из множеств можно составлять различные алгебраические выражения. Пусть в результате некоторых операций над одними и теми же множествами X,Y,Z получены новые множества U и V, содержащие одни и те же элементы. Выражение U=V представляет собой тождество алгебры множеств.

Рассмотрим наиболее важные тождества алгебры множеств.

1. XY=YX

2. XY=YX Коммутативные

3. XY=YX законы

4. X(YZ)=(XY)Z Ассоциативные

5. X(YZ)=(XY)Z законы

6. (XY)Z=(XZ)( YZ) Дистрибутивные

7. (XY)Z=(XZ)( YZ) законы

8. =Тождества

9. = де Моргана

Все приведенные тождества могут быть легко доказаны, например, с помощью диаграмм Эйлера-Венна. В качестве примера рассмотрим доказательство дистрибутивного закона (тождество 6).

Рис.3. Геометрическая иллюстрация тождества 6.

На рис.3а двойная штриховка соответствует выражению (XY)Z, на рис.3б заштрихованная область равна (XZ)(YZ). Из диаграмм видно, что оба выражения определяют одно и то же множество.