5.2.3. Моменты системы случайных величин

Начальный момент порядка k случайной величины Х может быть определен по формуле

Для величины Y:

Центральные моменты порядка k определяются формулами:

Например, средние значения для каждой из величин X и Y равны:

Дисперсии величин X и Y могут быть подсчитаны по формулам:

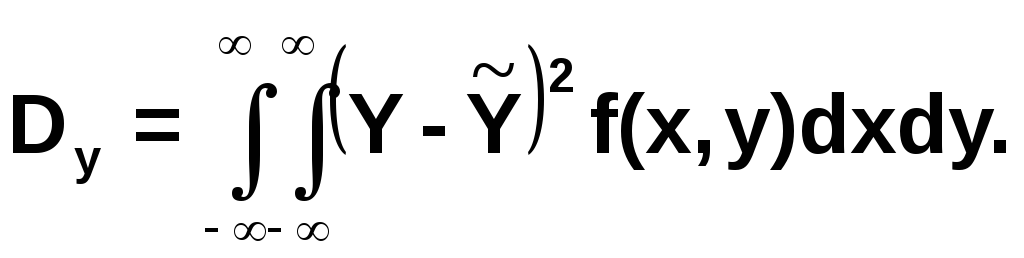
Смешанным моментом порядка r, s системы случайных величин X, Y называется математическое ожидание величины x^ry^s:

Очевидно, что при s=0, либо r=0 формула дает моменты случайной величины X и Y по отдельности.

Смешанным центральным моментом порядка r, s случайных величин X, Y называется математическое ожидание величины

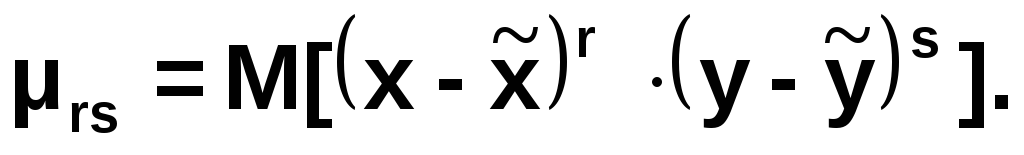
Очевидно, что при s=0 или r=0 формула дает центральные моменты случайных величин X и Y по отдельности.

Особую роль играет центральный смешанный момент первого порядка ₁₁, который называется корреляционным моментом:

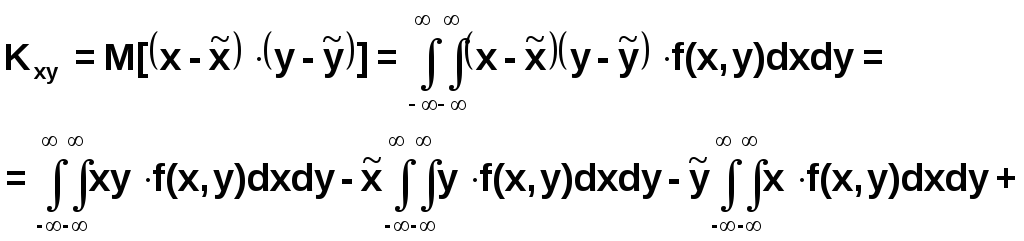
Коэффициентом корреляции случайных величин Х,Y называется безразмерная величина

Важным свойством коэффициента корреляции является следующее:

| R_xy | ≤ 1.

Коэффициент корреляции и корреляционный момент независимых случайных величин равен нулю. Случайные величины Х и Y называются коррелированными, если их корреляционный момент отличен от нуля. Они называются некоррелированными, если К_ху=R_xy=0. Независимые величины всегда некоррелированы. Зависимые величины могут быть как коррелированными, так и некоррелированными. При ряде обычных законов распределения понятия некоррелированные и независимые совпадают. В частности, для того, чтобы две величины, подчиненные нормальному закону, были взаимно независимы, необходимо и достаточно, чтобы R_xy=0.

Величина R_xy определяет степень коррелированности (связанности) случайных величин. Если абсолютное значение R_xy=1, то случайные величины являются полностью коррелированными. При этом случайные величины X и Y связаны между собой линейной зависимостью. Знак R_xy определяет характер связанности случайных величин. Положительный знак R_xy означает, что при отклонении одной из случайных величин от ее математического ожидания другая случайная величина будет иметь в среднем тенденцию к отклонению от своего математического ожидания по знаку в ту же сторону, что и первая случайная величина. Эта тенденция будет проявляться тем сильнее, чем ближе к единице будет значение R_xy. Наоборот, отрицательное значение R_xy означает, что при отклонении одной из случайных величин от ее математического ожидания другая случайная величина будет иметь в среднем тенденцию к отклонению от своего математического ожидания по знаку в другую сторону по сравнению с первой случайной величиной. Эта тенденция будет проявляться тем сильнее, чем ближе к -1 будет значение R_xy.

5.3. Случайные функции. Многомерные законы распределения

Случайной функцией (процессом) называется функция, значения которой при каждом данном значении аргумента являются случайной величиной. В результате опытов случайная функция принимает различные конкретные формы - это реализации случайной функции. Случайную функцию можно рассматривать как бесконечную совокупность случайных величин, зависящих от одного или нескольких непрерывно изменяющихся параметров. Случайные функции времени называются стохастическими процессами. Случайный процесс не есть определенная кривая (рис.61). Это такая функция времени, значения которой в каждый момент времени являются случайной величиной. Предсказать протекание одной реализации случайного процесса нельзя. Можно сделать лишь предсказание статистического характера относительно множества реализа-

Рис.61. Реализации случайного процесса

ций, протекающих в одинаковых условиях, т.е. случайный процесс может быть оценен некоторыми вероятностными характеристиками, например, законами распределения. Так как при каждом данном значении аргумента t значение случайной функции x(t) является случайной величиной, то полной вероятностной характеристикой этого значения является его закон распределения, который называется одномерным законом распределения. Этот закон зависит от t как от параметра и может быть задан одномерной плотностью вероятности f(x,t). Это функция времени, ибо вероятностное распределение с течением времени может меняться.

Произведение f(x,t)dx дает вероятность того, что в момент времени t величина X находится в интервале (x<X<x+dx). Эту величину можно найти приближенно экспериментальным путем, если наблюдать в момент времени t ряд систем, находящихся в одинаковых условиях. Для каждого данного t в отдельности будет свой закон распределения, причем для каждого из них

Одномерный закон распределения случайной функции является достаточной характеристикой случайной функции для тех задач, в которых значения случайной функции при различных значениях аргумента рассматриваются изолировано друг от друга. Для того, чтобы определить связь между возможными значениями случайной функции x(t) в различные моменты времени, вводится двумерный закон распределения, который задается двумерной плотностью вероятности: f(x₁,x₂,t₁,t₂). Это характеристика системы двух случайных величин x(t₁), x(t₂)- двух сечений случайной функции x(t) в произвольные моменты времени t₁ и t₂.