6.3. Прямая линия в пространстве r3

Положение прямой в пространстве R³ может быть определено заданием: а) любых двух точек; б) ee точки и вектора , параллельного этой прямой; в) двух пересекающихся плоскостей.

6.3.1. Векторное уравнение прямой

Рассмотрим произвольную прямую . Отметим точку и приложенный к точке . Произвольную (текущую) точку обозначим М. (Рис.6.10.) Вектор ={ m; n; p} называется направляющим вектором прямой.

Вектор т.к. и коллинеарные

(6.22.) — векторное уравнение прямой.

Рис.6.10.

Если известны координаты точек: и 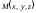, то в координатной форме (6.22.) имеет вид:

(6.23.) — параметрическое уравнение прямой.

6.3.2. Канонические уравнения прямой

Исключая параметр t из (6.23.) получим:

(6.24.)

где m, n, p — одновременно не равны нулю.

Задача 6.3.1. Составить уравнение прямой проходящей через две данные точки _,

Решение: В качестве направляющего вектора прямой можно взять вектор .

Поскольку прямая проходит через точку , то ее каноническое уравнение запишем в соответствии с (6.24.):

(6.25.) - называется уравнением прямой по двум ее точкам.

6.3.3. Прямая как линия пересечения двух плоскостей

Всякие две пересекающиеся плоскости и заданные уравнениями:

(6.26.)

определяют линию их пересечения.

Уравнения (6.26.) называют общими уравнениями прямой. Если плоскость непараллельна плоскости то :Ю.

Чтобы из (6.26.) получить каноническое уравнение надо найти: 1) точку, удовлетворяющую одновременно двум уравнениям; 2) направляющий вектор.

Найдем точку, удовлетворяющую уравнениям (6.26.), из системы найдется определитель не равный нулю:

Пусть то (6.26.) записываем в виде:

Пусть . Решив данную систему находим , .Любой вектор лежащий на прямой перпендикулярен нормалям плоскостей ,

, т.е.

Отсюда каноническое уравнение имеет вид

.

Пример 6.3.1. Составить каноническое уравнение прямой

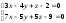
Решение: Найдите точку , удовлетворяющую данной системе:

1) Положив , , Решив систему получим:, .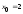

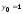Точка _{. Координаты нормальных векторов заданных плоскостей . Найдем направляющий вектор прямой:}

Подставим найденные величины в уравнение (6.24.).

Следовательно каноническое уравнение имеет вид:

.

6.3.4. Угол между двумя прямыми

Углом между двумя прямыми называется угол между их направляющими векторами.

Обозначим угол между направляющими векторами данных прямых через , направляющие вектора имеют координаты:

(6.27.)

6.3.5. Условия параллельности и перпендикулярности прямых

Если прямые параллельны то векторы и колиинеарные, и их коэффициенты пропорциональны.

(6.28.) – условие параллельности двух прямых в пространстве R3.

Если прямые перпендикулярны то , т.е. скалярное произведение равно нулю.

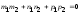_{(6.29) - условие перпендикулярности двух прямых в пространстве R3.}

_{Контрольные вопросы и задания.}

1. _{Какой вектор называется направляющим вектором прямой?}

2. _{Чем определяется положение прямой в пространстве R3?}

3. _{Запишите канонические уравнения прямой.}

4. _{Составьте уравнение прямой по двум ее точкам.}

5. _{Как перейти от общих уравнений прямой к ее каноническому уравнению?}

6. _{Как найти угол между двумя прямыми?}

7. _{Назовите условие параллельности и перпендикулярности прямых в R3.}

_{Задачи для самостоятельной работы.}

1. Прямая задана общими уравнениями:

записать ее канонические уравнения.

2. Вычислить величину угла между прямыми

3. Найти точку пересечения двух прямых

4. Найти уравнение прямой, проходящей через точку M(0,3,-2) и пересекающей прямые:

5. Найти проекцию точки M(0,1,2)на прямую x=1+2t, y=-1+3t, z=2+t

6. Найти точку M΄, симметричную данной точке M(4,3,10) относительно прямой (x-1)/2=(y-2)/4=(z-3)/5