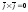- •Основы линейной, векторной алгебры и аналитической геометрии
- •Содержание.
- •Обозначения, используемые в пособии.
- •1.3.Транспонирование матриц
- •Операция транспонирования обладают следующими свойствами:
- •1.4. Понятие определителя.
- •1.5. Минор. Теорема Лапласа. Определение 1.5.1.
- •Свойства определителей
- •1.7 Обратные матрицы
- •Достаточность: Пусть Рассмотрим элементы с определяются как
- •4)Обратная матрица единственна
- •1.8 Ранг матрицы Определение 1.8.1.
- •Определение 1.8.2.
- •2. Системы линейных алгебраических уравнений
- •2.1. Основные понятия
- •2.2 Крамеровские системы
- •Пример 2.2.2. Решить по формулам Крамера систему уравнений:
- •2.3 Системы линейных уравнений общего вида
- •2.4 Однородные системы линейных уравнений
- •Пример 2.4.1 Решить систему:
- •3. Основы численных методов решения задач теории матриц и систем линейных алгебраических уравнений .
- •3.1 Элементарные преобразования матриц
- •Действительно:
- •3.2 Вычисление определителя
- •3.3 Вычисление ранга матрицы
- •3.4 Решение систем линейных уравнений
- •3.5 Нахождение обратной матрицы.
- •4. Линейные векторные пространства
- •4.1 Понятие линейного пространства
- •4.2 Линейная зависимость системы векторов
- •4.3. Базис и размерность линейного пространства.
- •4.4. Координаты вектора
- •Пример 4.4.1.
- •4.5. Евклидово пространство
- •4.6. Ортогональность векторов в Еп.
- •5. Вектора в трёхмерном пространстве .
- •5.1. Угол между двумя векторами. Проекция вектора на ось.
- •5.2. Координаты вектора заданного двумя точками.
- •5.3.Условие коллинеарности двух векторов в координатной форме
- •5.4. Скалярное произведение векторов в координатной форме
- •5.5. Определение длины вектора и угла между двумя векторами.
- •5.6. Направляющие косинусы вектора
- •5.7. Векторное произведение двух векторов
- •5. 8. Смешанное произведение трех векторов
- •5.9. Свойства смешанного произведения
- •Элементы аналитической геометрии.
- •6.1. Прямая на плоскости.
- •Уравнение прямой в отрезках
- •6.2.3. Уравнение плоскости в отрезках
- •6.2.4. Уравнение плоскости проходящей через три точки
- •6.2.5.Угол между двумя плоскостями
- •6.2.6. Условия перпендикулярности и параллельности плоскостей
- •6.2.7. Расстояние от точки до плоскости
- •6.3. Прямая линия в пространстве r3
- •6.3.1. Векторное уравнение прямой
- •6.3.2. Канонические уравнения прямой
- •6.3.3. Прямая как линия пересечения двух плоскостей
- •6.3.4. Угол между двумя прямыми
- •6.3.5. Условия параллельности и перпендикулярности прямых
- •6.4. Прямая и плоскость в пространстве
- •6.4.1. Пересечение прямой и плоскости в пространстве r3
- •6.4.2.Условие параллельности и перпендикулярности прямой и
- •6.4.3.Угол между прямой и плоскостью
- •7. Кривые второго порядка
- •7.1.Окружность
- •7.2. Эллипс
- •7.3.Гипербола
- •7.4.Парабола
- •7.5. Уравнения кривых второго порядка с осями симметрии параллельными осям координат.
- •8. Поверхности второго порядка
- •8.1.Цилиндрические поверхности с образующими, параллельными координатной оси
- •8.2.Цилиндры второго порядка
- •8.3.Поверхности вращения
- •8.4. Поверхности второго порядка заданные каноническими уравнениями
- •8.4.1. Эллипсоид
- •8.4.2.Гиперболоиды
- •8.4.3. Параболоиды Эллиптический параболоид.
- •Гиперболический параболоид.
- •8.4.4. Конус второго порядка
- •9. Расчетные задания.
- •9.1. Линейная и векторная алгебра.
- •9.2. Аналитическая геометрия.
- •10. Тестовые задания для самостоятельной работы.
- •Задание 3. Найдите матрицу х из уравнений:
- •Задание 4. С помощью формул Крамера решить систему уравнений:
- •Задание 9. Найти координаты вектора векторного произведения векторов a и b.
- •2. Найти точку пересечения прямой и плоскости.
5.6. Направляющие косинусы вектора
Пусть в
пространстве с заданной прямоугольной
системой координат задан ненулевой
вектор
 (см. Рис.5.5.).
(см. Рис.5.5.).
z

M
γ
β
O y
α
Рис.5.5.
Направление
вектора в пространстве определяется
углами
 ,
которые вектор составляет с осями
координат. Косинусы этих углов называются
направляющими .
,
которые вектор составляет с осями
координат. Косинусы этих углов называются
направляющими .
Если вектор
 задан
координатами
задан
координатами
 ={x;y;z}
или
={x;y;z}
или
 ,
,
где
 - орты координатных осей, то x,y,z
являются проекциями вектора
- орты координатных осей, то x,y,z
являются проекциями вектора
 на координатные оси OX,
OY, OZ
в соответствии с теоремой 5.1.1. получим
следующие равенства:
на координатные оси OX,
OY, OZ
в соответствии с теоремой 5.1.1. получим
следующие равенства:


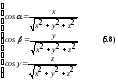
Возведем обе
части соотношений (5.8.) в квадрат и сложим,
получим:
 .
.
Сумма квадратов направляющих косинусов любого вектора равна единице.
Для единичного вектора


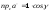
разложение его
по осям координат имеет вид:
 .
.
Пример 5.6.1. На
точку действуют три силы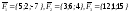 Найти величину и направление
равнодействующей силы
Найти величину и направление
равнодействующей силы
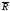 .
.
Решение: Так
как
 то R={20,9,12} тогда величина
то R={20,9,12} тогда величина
 равна
равна а ее направление определяется направляющими
косинусами
а ее направление определяется направляющими
косинусами

Контрольные вопросы и задания.
-
Запишите условие коллениарности векторов.
-
Дайте определение скалярного произведения.
-
Перечислите свойства скалярного произведения.
-
Что определяют направляющие косинусы вектора?
-
Какому условию должны удовлетворять ненулевые векторы
 и
и
 ,
чтобы вектор
,
чтобы вектор
 был
ортоганален вектору
был
ортоганален вектору
 ?
? -
Доказать, что скалярное произведение двух векторов не изменится, если к одному из них прибавить вектор, ортогональный другому сомножителю.
-
Найти величину угла между биссектрисами углов XOY и XOZ.
-
Какая тройка векторов называется правой?
Задачи для самостоятельной работы.
-
Вычислить скалярное произведение векторов
 и
и
 ,
если векторы
,
если векторы
 и
и
 образуют
угол
образуют
угол
 и
и

-
Вычислить величину угла между векторами
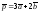 и
и ,
где
,
где и
и
 –
единично взаимно перпендикулярные
векторы.
–
единично взаимно перпендикулярные
векторы. -
Даны вершины треугольника A(-1, -2, 4), B(-4, -2, 0) и C(3, -2, 1).Определить величину его внутреннего угла при вершине B.
-
Даны три силы
 .
Найти величину, направление равнодействующей
силы R и работу, которую она производит,
когда точка
.
Найти величину, направление равнодействующей
силы R и работу, которую она производит,
когда точка
 ее приложения, двигаясь прямолинейно
перемещается в положение
ее приложения, двигаясь прямолинейно
перемещается в положение .
. -
Найти угол между диагоналями параллелограмма, построенного на векторах
 и
и
 .
. -
Найти вектор
 ,
зная, что он перпендикулярен векторам
a={2,3,-1} и b={1,-2,3} и удовлетворяет
условию (x,2i-j+k) = -6 .
,
зная, что он перпендикулярен векторам
a={2,3,-1} и b={1,-2,3} и удовлетворяет
условию (x,2i-j+k) = -6 . -
К некоторой точке приложены две силы, действующие под углом 120, причем
 .
Найти величину равнодействующей силы.
.
Найти величину равнодействующей силы.
5.7. Векторное произведение двух векторов
Определение
5.7.1. Векторным произведением вектора
 на
вектор
на
вектор
 называется вектор
называется вектор
 ,
удовлетворяющий следующим условиям:
,
удовлетворяющий следующим условиям:
-
вектор
 перпендикулярен
векторам
перпендикулярен
векторам
 и
и
 ,
т.е.
,
т.е.
 ;
;

Рис. 5.6.
2) модуль вектора
 численно равен площади параллелограмма,
построенного на перемножаемых векторах
численно равен площади параллелограмма,
построенного на перемножаемых векторах
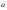 и
и
 ,
как на сторонах, т.е.
,
как на сторонах, т.е.
 ;
;
3) упорядоченная
тройка векторов( )
является правой. В определении
предполагается что
)
является правой. В определении
предполагается что .
.
Свойства векторного произведения
-
При перестановке сомножителей векторное произведение меняет свой знак, сохраняя модуль.

 — правая тройка
— правая тройка
 — левая тройка.
— левая тройка.
 направлены противоположно
направлены противоположно

Рис.5.7.
2) Сочетательное свойство относительно скалярного множителя или векторное умножение ассоциативно относительно умножения на число, т.е.

3) Распределительное свойство или векторное умножение дистрибутивно относительно операции сложения векторов:
 .
.
4) Если
 и
и
 ,
не равны нулю
,
не равны нулю
 ,
то
,
то
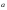 и
и
 коллинеарные вектора
коллинеарные вектора
 .
.
Для того чтобы
два ненулевых вектора
 и
и
 были коллинеарны, необходимо и достаточно
чтобы их векторное произведение равнялось
нуль вектору.
были коллинеарны, необходимо и достаточно
чтобы их векторное произведение равнялось
нуль вектору.
5) Векторное
произведение векторов
 :
:
|
a) |
б) |
|
|
|
|
|
|
в)  .
.
6) Векторное произведение в координатной форме:
Пусть  ,
, 
Умножим применив
третье свойство, а затем пятое:
применив
третье свойство, а затем пятое:



 .
.
Пример 5.7.1. Найти
площадь параллелограмма построенного
на векторах
 и
и
 .
.
Решение:

 кв. ед.
кв. ед.
Пример 5.7.2. Сила P={2;-4;5} приложена к точке M0(4;-2;3). Определить момент этой силы относительно точки A(3;2;-1).
Решение:
Момент силы P
относительно точки A
есть вектор
 .
Найдем координаты
.
Найдем координаты
 :
:
 ={1;-4;4}
и координаты
вектора
={1;-4;4}
и координаты
вектора
 :
:

Контрольные вопросы и задания.
-
Дайте определение векторного произведения.
-
Перечислите свойства векторного произведения.
-
Доказать, что векторное произведение не изменится, если к одному из сомножителей прибавить вектор, коллениарный другому сомножителю.
-
Запишите условие коллениарности векторов.
-
Найдите единичный вектор
 ,
одновременно перпендикулярный вектору
,
одновременно перпендикулярный вектору
 и
оси абсцисс.
и
оси абсцисс.
Задачи для самостоятельной работы.
-
Найти координаты вектора [2a+b,b], если a={3,-1,-2}, b={1,2,-1} .
-
Вычислить площадь Sпараллелограмма, построенного на векторах a={8,4,1} и b={2,-2,1} .
-
Найти площадь S треугольника, построенного на векторах a=i-2j+5k и b=5j-7k .
-
Сила P={2,-4,5} приложена к точке M0(4,-2,3). Определить момент этой силы относительно точки A(3,2,-1).
-
Вектор m , перпендикулярный оси аппликат и вектору a=8i-15j+3k, образует острый угол с осью абсцисс. Зная, что
 ,
найти его координаты.
,
найти его координаты. -
Сила Q={3,4,-2} приложена к точке C(2,-1,-2). Определить величину и направление момента этой силы относительно начала координат.
-
Вектор m, перпендикулярный оси аппликат и вектору
 , образует острый угол с осью абсцисс.
Зная, что
, образует острый угол с осью абсцисс.
Зная, что
 ,
найти его координаты.
,
найти его координаты. -
Найти момент силы
 относительно
начала координат, если точка ее приложения
A(1,1,1). Определить также
направляющие косинусы момента.
относительно
начала координат, если точка ее приложения
A(1,1,1). Определить также
направляющие косинусы момента.