3.2. Преобразования сигнала

Для преобразования аналогового сигнала в дискретный используется процедура, которая называется квантованием. Различают два вида квантования – по времени и по уровню (дискретизацию).

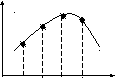
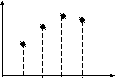
Квантование по времени – замена непрерывной (по времени и по уровню) функции x(t) (рис. 3.1а) некоторым множеством непрерывных (по уровню) функций x(t_i) (на рис. 3.1б i = {1,2,3,4}).

x x

x(t₃) x(t₃)

x(t₂) x(t₄) x(t₂) x(t₄)

x(t₁) x(t₁)

x(t)

t₁ t₂ t₃ t₄ t t₁ t₂ t₃ t₄ t

а) б)

Рис. 3.1. Иллюстрация к квантованию по времени:

а) аналоговый сигнал x(t) до квантования;

б) дискретный (по времени) сигнал x(t) – результат квантования.

Очевидно, дискретизация связана с потерей информации. В самом деле, дискретный сигнал на рис. 3.1б не показывает, как ведет себя исходный сигнал в моменты времени, например, между t₃ и t₄. Иначе говоря, дискретизация связана с некоторой погрешностью , которая зависит от шага дискретизации t = t_i – t_i-1: при малых значениях шага дискретизации число точек замера высоко, и теряется мало информации; очевидно, картина обратная при больших шагах дискретизации. Погрешность дискретизации  в каждый момент времени t определяется по формуле:

(t) = x(t) – v(t), (3.1)

где v(t) – функция восстановления, которая по дискретным значениям восстанавливает x(t).

Виды дискретизации различаются по регулярности отсчетов:

• равномерная дискретизация, когда t постоянно;

• неравномерная дискретизация, когда t переменно, причем этот вид, в свою очередь, делится на подвиды:

• адаптивную, когда t меняется автоматически в зависимости от текущего изменения сигнала. Это позволяет увеличивать шаг дискретизации, когда изменения сигнала x(t) незначительны, и уменьшать – в противном случае;

• программируемую, когда t изменяется оператором или в соответствии с заранее выставленными условиями, например, в фиксированные моменты времени.

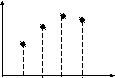
Квантование по уровню - преобразование непрерывных (по уровню) сигналов x(t_i) в моменты отсчета t_i в дискретные. В результате непрерывное множество значений сигнала x(t_i) в диапазоне от x_min до x_max преобразуется в дискретное множество значений x_k – уровней квантования (рис. 3.2). Шаг квантования x определяется по формуле:

x = x_j – x_j-1 .

Можно сказать, что квантование по уровню – это измерение сигнала. В самом деле, по рис. 3.2б видно, что сигнал x(t₁) составляет 0 уровней квантования (k = 0), а сигнал x(t₄) – 2 уровня квантования (k = 2).

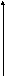
x(t) x(t)

x₂

x(t₃) x_max x(t₃)

x

x₁

x_min

(t₂) x(t₄) x(t₂) x(t₄)

x(t₁) x(t₁)

t₁ t₂ t₃ t₄ t t₁ t₂ t₃ t₄ t

а) б)

Рис. 3.2. Иллюстрация к квантованию по уровню:

а) аналоговые по уровню (но дискретные по времени) сигналы x(t_i) до квантования;

б) квантованные по уровню сигналы x(t_i).

При квантовании по уровню не всегда сигнал x(t_i) совпадает с уровнем квантования (см. сигнал x(t₂) на рис. 3.2б). В таком случае поступают одним из следующих способов:

1. x(t_i) отождествляют с ближайшим значением (в нашем примере – с x₂);

2. x(t_i) отождествляют с ближайшим меньшим (или большим) значением. Тогда при отождествлении с ближайшим большим значением сигнал x(t₂) отождествится с x₂ независимо от того, насколько близко он к этому уровню квантования находится. При отождествлении с ближайшим меньшим значением сигнал x(t₂) отождествится с x₁ также независимо от того, насколько близко он к этому уровню квантования находится.

Очевидно, и при квантовании по уровню возникает погрешность квантования (x_k):

(x_k) = x(t_i) - x_k. (3.2)

Погрешность квантования по уровню тем меньше, чем меньше шаг квантования.

Виды квантования по уровню:

1. равномерное, когда диапазон изменения сигнала разбивается на m одинаковых частей. Тогда, зная размер шага квантования, для представления x_k достаточно знать число k.

2. неравномерное, когда диапазон изменения сигнала разбивается на m различных частей.