4.4.3. Коды, исправляющие ошибки

Особое значение имеют помехозащитные коды, которые могут исправлять ошибки определенной кратности. Соотношение между максимальной кратностью исправляемой ошибки q и кодовым расстоянием d определяется по формуле (4.7):

d  2q + 1. (4.7)

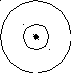
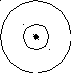
В основу исправления ошибок положена следующая идея: определяется множество кодовых комбинаций, включающее все разрешенные и те запрещенные, которые получены при искажении ошибкой кратности не более q. Это множество разбивается на m подмножеств, где m – число исходных кодируемых символов. В каждое подмножество входят: разрешенная кодовая комбинация и ближайшие к ней запрещенные, которые отстоят от разрешенной на расстояние не больше q. Например, при построении помехозащитного кода для двух символов, способного исправлять ошибки кратности не больше q, подобное разбиение может выглядеть так, как показано на рис. 4.7.

q q

….. 1 …..

Рис. 4.7. Иллюстрация к принципу исправления ошибок в помехозащитном коде

Здесь центры окружностей – разрешенные кодовые комбинации, окружности с минимальным радиусом – множество кодовых комбинаций, отстоящих от разрешенной на расстояние, равное 1; окружности с радиусом q - множество кодовых комбинаций, отстоящих от разрешенной на расстояние, равное q; промежуточные окружности (показаны многоточием) – содержат кодовые комбинации, отстоящие от разрешенной на расстояние, равное их радиусу (от 1 до q). Расстояние между внешними окружностями, равное 1, вводится для различения подмножеств.

Тогда при декодировании определяется, в какое подмножество входит принятая кодовая комбинация. Если она является разрешенной, то сразу декодируется; если запрещенная, то исправляется на разрешенную, с которой находится в одном подмножестве, а затем декодируется.

Пример 4.10. Построить помехозащитный код, исправляющий ошибку кратности 1, для передачи двух символов: a и b.

Построим первичный код. Поскольку для кодирования двух символов достаточно одного двоичного разряда, первичный код может иметь следующий вид:

a 0,

b 1.

В силу (4.7) и поскольку по заданию q = 1, имеем d = 3, таким образом, для исправления ошибки кратности 1 кодовое расстояние должно быть равно по меньшей мере 3.

Поскольку в первичном коде обеспечено расстояние между кодовыми комбинациями, равное 1, для выполнения условия d = 3 необходимо, чтобы проверочные разряды обеспечивали расстояние между кодовыми комбинациями, по меньшей мере, равным 2.

Очевидно, для этого число проверочных разрядов должно быть не меньше 2. Тогда разрешенные кодовые комбинации могут иметь вид:

исходный информационный проверочные результирующий

символ разряд разряды код

a 0 00 000

b 1 11 111

Очевидно, кодовое расстояние равно 3, а построенные кодовые комбинации являются разрешенными.

Определим общее число всевозможных комбинаций, если число разрядов кода равно 3:

000 - разрешенная кодовая комбинация,

001

010

0

- запрещенные кодовые комбинации,

11

100

101

110

111 - разрешенная кодовая комбинация.

Определим подмножества кодовых комбинаций, которые отстояли бы от каждой разрешенной на минимальное расстояние, равное 1:

для 000 для 111

001 011

010 101 (4.8)

100. 110.

Пусть передается кодовая комбинация 000 (символ a) и на нее накладывается ошибка кратности 1. В табл. 4.15 показаны полученные кодовые комбинации и их декодирование.

Таблица 4.15

Передаваемая кодовая комбинация	Ошибка	Принимаемая кодовая комбинация	Результат исправления (см. (4.8))	Результат декодирования
000	100	100	000	a
000	010	010	000	a
000	001	001	000	a

Таким образом, построенный код позволяет исправлять ошибки кратности 1.

Пример 4.11. Построить помехозащитный код, исправляющий ошибку кратности 1, для передачи символов: a, b и c.

Построим первичный код: a – 00; b – 01; c – 10.

Для решения поставленной задачи необходимо обеспечить d = 3 (см. пример 4.10).

Воспользуемся схемой формирования кода Грея из примера 4.9:

	00	01	11
000	a
011		b
101			c

Таким образом, получены коды:

a  00000, b  01101, c 10111.

Полученное кодовое расстояние d = min {d_ab, d_ac, d_bc} = min {3, 4, 3} = 3 обеспечивает исправление ошибки кратности q = 1.

Рассмотрим, как исправляются ошибки в данном случае. Все множество кодовых комбинаций пятиразрядного двоичного кода равно 2⁵ = 32. Из них три кодовые комбинации – разрешенные, остальные – запрещенные. Разобьем кодовые комбинации на три подмножества, в каждое из которых будут входить: одна разрешенная и те запрещенные, которые отстоят от разрешенной на расстояние в 1. Имеем:

для 00000 для 01101 для 10111

00001 01100 10110

00010 01111 10101

00100 01001 10011 (4.9)

01000 00101 11111

10000 11101 00111

Очевидно, общее число кодовых комбинаций, включенных в построенные подмножества, равно 24. Оставшиеся 8 кодовых комбинаций являются следствием ошибки кратности больше 1 и в сформированные подмножества не включены.

Проверим, как выполняется исправление ошибки кратности 1. Пусть передается кодовая комбинация 01101 (символ b) и на нее накладывается ошибка кратности 1. В табл. 4.16 показаны полученные кодовые комбинации и их декодирование.

Таблица 4.16

Передаваемая кодовая комбинация	Ошибка	Принимаемая кодовая комбинация	Результат исправления (см. (4.9))	Результат декодирования
01101	10000	11101	01101	b
01101	01000	00101	01101	b
01101	00100	01001	01101	b
01101	00010	01111	01101	b
01101	00001	01100	01101	b

Пусть на ту же кодовую комбинацию накладывается ошибка кратности 2 (табл. 4.17). Результирующие кодовые комбинации либо невозможно декодировать, либо декодирование неверно.

Таблица 4.17

Передаваемая кодовая комбинация	Ошибка	Принимаемая кодовая комбинация	Результат декодирования
01101	10001	11100	Невозможно декодировать
01101	01001	00100	То же
01101	00101	01000	a
01101	00011	01110	Невозможно декодировать
01101	10010	11111	с
01101	01010	00111	То же
01101	00110	01011	Невозможно декодировать
01101	10100	11001	То же
01101	01100	00001	а
01101	11000	10101	с

В заключение отметим, что для обнаружения ошибки кратности q₁ и исправления ошибки кратности q₂ (q₁  q₂) минимальное кодовое расстояние должно удовлетворять следующему соотношению:

d  q₁ + q₂ + 1.