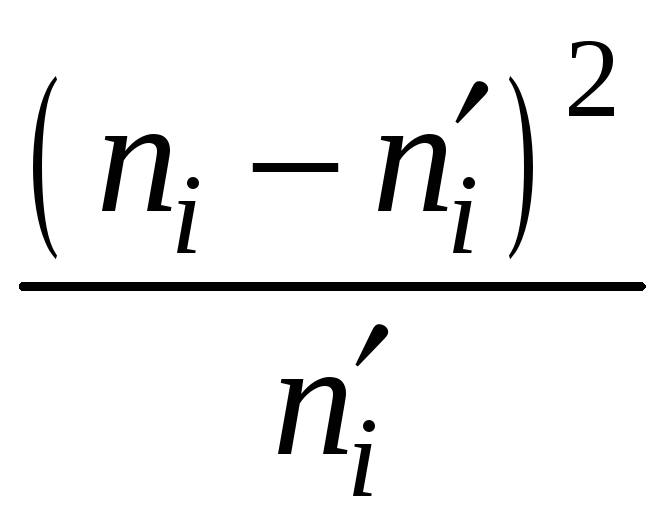1.4.1. Критерій узгодження к.Пірсона

Критерій узгодження Пірсона застосовується для зіставлень емпіричного розподілу ознаки з теоретичним – рівномірним, нормальним або якимось іншим, а також для зіставлення двох, трьох і більше емпіричних розподілів тієї самої ознаки.

Обмеження для достовірного застосування цього критерію є такими:

1. Обсяг вибірки повинен бути більше 30.

2. Теоретична частота для кожного часткового інтервалу (або групи значень) не повинна бути менш п'яти.

3. Обрані класи інтервалів повинні «вичерпати» весь розподіл, тобто охоплювати весь діапазон варіативності ознаки. При цьому групування на інтервали повинно бути однаковим у всіх розподілах, що зіставляються.

4. Необхідно вносити «виправлення на неперервність» при зіставленні розподілів ознак, які приймають усього два значення.

5. Часткові інтервали (або групи значень) повинні бути не перехресними: якщо спостереження віднесене до одного інтервалу, то воно вже не може бути віднесено ні до якого іншого.

За міру розбіжності між теоретичною і емпіричною функціями розподілу відповідно до критерію Пірсона приймають статистику

. (21)

Тут – емпіричні частоти, – теоретичні частоти, – число інтервалів статистичного ряду, – обсяг вибірки. Зрозуміло, що чим менше різниці , тим ближче теоретичний розподіл до емпіричного, тому, чим менше значення критерію , тим з більшою вірогідністю можна стверджувати, що емпіричний і теоретичний розподіл підпорядковані одному закону.

Критерій визначає, чи з однаковою частотою зустрічаються різні значення ознаки в емпіричному і теоретичному розподілах або в двох і більше емпіричних розподілах. Чим більше розбіжності між двома розподілами, що розглядаються, тим більше емпіричне значення .

Схема застосування критерію Пірсона:

• обчислюють величину 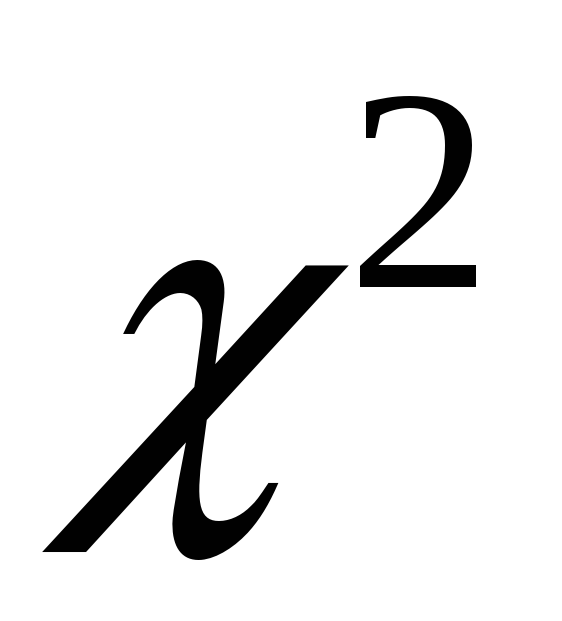–статистику за формулою (21);

• по таблицях критичних точок Пірсона (додаток 4) знаходять значення , де число параметрів теоретичного розподілу, оцінки яких були обчислені по ЕД (у випадку нормального або рівномірного розподілу , для розподілу Пуассона ), 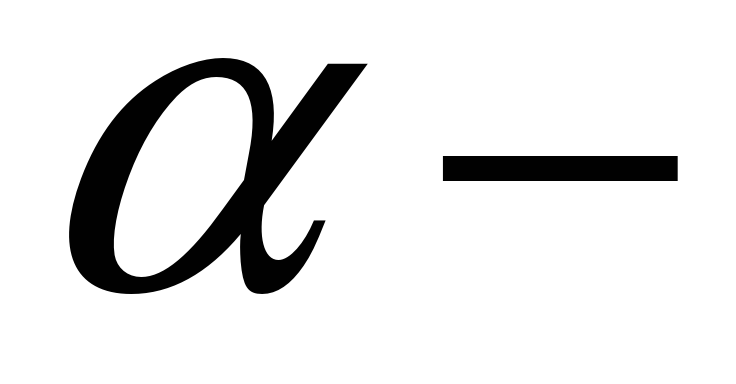рівень значущості, що характеризує величину припустимої похибки (звичайно 0,01; 0,05; 0,1);

• порівняння отриманих величин:

• якщо , то при заданому рівні значущості можна стверджувати, що статистичні дані розподілені за даним законом розподілу, і отримана розбіжність між теоретичними і емпіричними частотами є випадковою за рахунок обмеженого об'єму вибірки;

• якщо , то розбіжність між теоретичними і емпіричними частотами не є випадковою, а свідчить про наявність істотної різниці між статистичним і теоретичним законами розподілу.

Слід зазначити, що критерієм Пірсона з достатньою точністю можна користуватися в тих випадках, коли об'єм вибірки досить великий і в кожному інтервалі число спостережень не менш п'яти . Перевірку правильності обчислень –статистики, яку визначає відношення (21), проводять за формулою .

Приклад 5: перевірка за критерієм Пірсона гіпотези про розподіл кількості значень згасань сигналу за законом Пуассона

У прикладі 1 побудовано теоретичні частоти в припущенні про розподіл досліджуваної ознаки за законом Пуассона. Перевірити узгодженість теоретичних і емпіричних частот за критерієм Пірсона.

	42	156	294	403	410	329	225	157	54	17	8	4	1
	38	154	308	410	410	328	219	125	63	28	11	4	2

Розв'язання: для коректного застосування критерію Пірсона об'єднаємо останні дві групи значень (тоді число спостережень стане не менш п'яти, як це потрібно для коректного застосування критерію). Проведемо допоміжні обчислення в табл.7.

Таблиця 7

Розрахунок –статистики

42	38	16	0,42	1764	46,42
156	154	4	0,03	24336	158,03
294	308	196	0,64	86436	280,64

Продовження таблиці 7

403	410	49	0,12	162409	396,12
410	410	0	0	168100	410
329	328	1	0,003	108241	330,003
225	219	36	0,16	50625	231,16
157	125	1024	8,19	24649	197,19
54	63	81	1,29	2916	46,29
17	28	121	4,32	289	10,32
8	11	9	0,82	64	5,82
5	6	1	0,17	25	4,17
			16,163		2116,163

Перевірка доводить правильність проведених обчислень

Закон Пуассона є однопараметричним (за ЕД визначають один параметр ), тому . Число інтервалів статистичного ряду , тоді по таблиці критичних точок Пірсона (див. додаток 4) для рівня значущості знаходимо

.

Оскільки , то гіпотезу про те, що кількість значень згасань сигналу розподілено за законом Пуассона, можна вважати правдоподібною і узгодженою з ЕД.