1.2.8. Розподіл Вейбула
Цей розподіл названий по прізвищах інженера В.Вейбула, який ввів його в практику аналізу результатів випробувань, і математика Б.В.Гнеденка, що одержав такий розподіл як граничний при вивченні максимального з результатів випробувань.
Нехай
–
випадкова величина,
що
характеризує тривалість функціонування
виробу,
складної системи, елемента, підприємства
або життя живої істоти. Опишемо типову
поведінку
інтенсивності відмови
,
де
і
– функція і щільність розподілу
випадкової величини
.
Весь інтервал часу можна розбити на три
періоди. На першому
з них (період «обкатування») функція
має високі значення і явну тенденцію
до спадання (найчастіше вона монотонно
спадає). Це можна пояснити наявністю у
розглянутій партії одиниць продукції
з
явними і прихованими дефектами, які
приводять до відносно швидкого виходу
з ладу цих одиниць продукції. Саме на
перший період звичайно поширюється
гарантійний строк.
Потім настає період нормальної експлуатації, що характеризується приблизно постійною і порівняно низькою інтенсивністю відмов. Природа відмов у цей період носить раптовий характер (аварії, помилки експлуатаційних працівників) і не залежить від тривалості експлуатації одиниці продукції.
В третій період експлуатації (період старіння і зношування) природа відмов складається з незворотних фізико-механічних і хімічних змін матеріалів, що приводять до прогресуючого погіршення якості одиниці продукції та остаточному виходу її з ладу.
Кожному
періоду
відповідає свій вид
функції
,
де
– певні числові параметри. Значення
,
,
відповідають виду
інтенсивності відмов у періоди
обкатування, нормальної експлуатації
і старіння відповідно.
Розподіл Вейбула–Гнеденка застосовується також при побудові ймовірнісних моделей ситуацій, у яких поведінку об'єкта визначають «найбільш слабкою ланкою»(страхові виплати або втрати через комерційні ризики, при вивченні границь пружності і витривалості сталі, ряду характеристик надійності).
Закон розподілу Вейбула описується диференціальною функцією
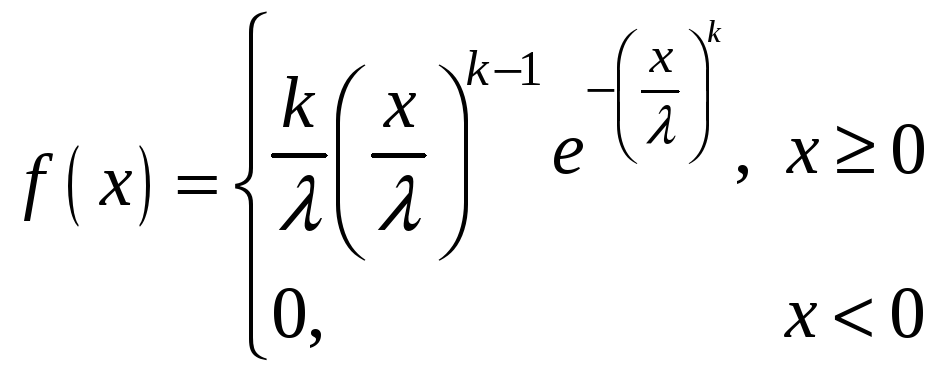(13)
Тут
і
– параметри розподілу. Величина
параметра
впливає на форму кривої розподілу,
заданої відношенням (13) (див. рис.13).
Рис.13. Розподіл Вейбула
Інтегральна
функція розподілу Вейбула
має вигляд
.
Характеристики випадкової величини,
розподіленої
за законом Вейбула,
такі: математичне сподівання
;
дисперсія
;
асиметрія
;
ексцес
,
де
.
При
розподіл Вейбула перетворюється в
експоненціальний, при
і
наближається до нормального. Розподіл
Вейбула широко застосовується при
розрахунку показників надійності,
зокрема, при дослідженні міцності і
довговічності деталей. Цьому закону
добре підпорядковуються розподіл
границь пружності ряду металів,
характеристики міцності і довговічності
деталей (підшипники кочення, напружені
осі і вали).
1.2.9. Гамма-розподіл
Випадкова величина, що має гамма-розподіл, описується щільністю ймовірності
(14)
Тут
і
– параметри розподілу,
–
одна з використовуваних у математиці
спеціальних функцій, так звана
«гамма-функція», по якій і названо цей
розподіл. Крива розподілу залежить від
двох параметрів закону (14)
і
(див.
рис.14).
а)
б)
Рис.14. Гамма-розподіл
Гамма-розподілена
випадкова величина
визначається
наступними характеристиками: математичне
сподівання
,
дисперсія
,
асиметрія
,
ексцес
,
де
і
– параметри розподілу.
Слід
зазначити, що гамма-розподіл (14) відповідає
експоненціальному розподілу
(12) при
.
Нормальний розподіл (9) є
граничним випадком гамма-розподілу при
.
Гамма-розподіл
широко застосовують в економіці і
менеджменті,
теорії і практиці надійності випробувань,
у різних областях
техніки і метеорології. Зокрема,
гамма-розподілу підпорядковані
в багатьох ситуаціях такі величини,
як загальний
термін служби виробу,
час досягнення виробом граничного стану
при корозії, час наробітки до
ої
відмови
.
Тривалість життя хворих хронічними
захворюваннями, час досягнення визначеного
ефекту при лікуванні в ряді випадків
мають гамма-розподіл. Це розподіл є
найбільш адекватним для опису попиту
в економіко-математичних моделях
управління
запасами.
Закон розподілу випадкової величини, яку вивчає дослідник, може бути визначено у першому наближенні за величиною коефіцієнта варіації (див.табл.1)
,
(15)
що вказує міру відносного розсіяння випадкової величини, тобто показує, яку долю середнього значення цієї величини складає її середнє розсіяння.
Таблиця 1
Закон розподілу випадкової додатної величини
в залежності від її коефіцієнта варіації
|
Границі зміни коефіцієнта
варіації
|
Закон розподілу випадкової
величини
|
|
|
нормальний |
|
|
гамма-розподіл |
|
|
Вейбула, Пуассона |
|
|
експоненціальний |
