1.2.7. Експоненціальний (показниковий) розподіл

Розглянемо "потік подій", тобто послідовність подій, що відбуваються одна за одною у якісь моменти часу. Прикладами можуть служити потік викликів на телефонній станції, потік відмов обладнання в технологічному ланцюжку, потік відмов виробів при випробуваннях продукції, потік звернень клієнтів у відділення банку, потік покупців, що звертаються за товарами і послугами. У теорії потоків подій справедлива теорема, аналогічна центральній граничній теоремі. Розглядається сумарний потік, що складено з великої кількості незалежних потоків, жоден з яких не має переважного впливу на сумарний потік. Наприклад, потік викликів, що надходять на телефонну станцію, складається з великої кількості незалежних потоків викликів, що надходять від окремих абонентів. Доведено, що у випадку, коли характеристики потоків не залежать від часу, сумарний потік цілком описується одним числом – інтенсивністю потоку.

Щільність експоненціального розподілу відмінна від нуля тільки для невід'ємних значень . У нулі вона приймає максимальне значення, яке дорівнює – параметр розподілу. Зі зростанням вона спадає, залишаючись угнутою, і асимптотично наближується до нуля. Вираз для щільності показникового розподілу такий

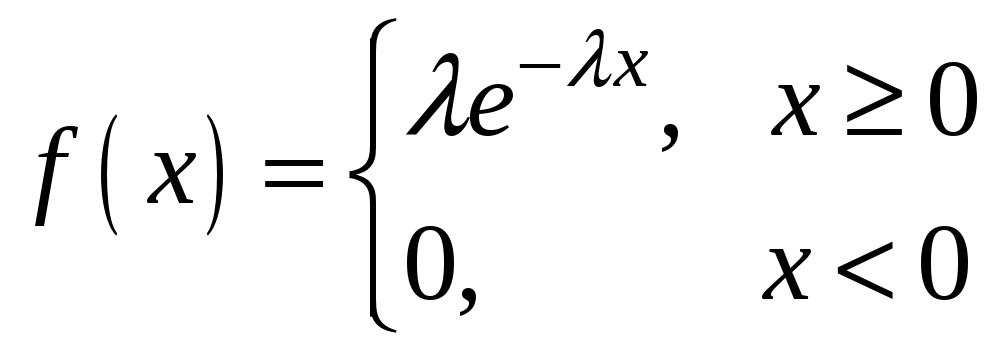
. (12)

Графік диференціальної функції розподілу (12) показано на рис.12.

Рис.12. Експоненціальний закон розподілу

Інтегральна функція має вигляд 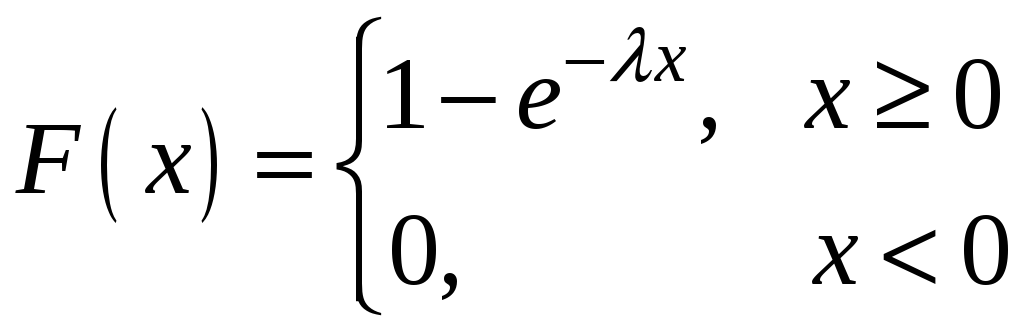. Це співвідношення має просту інтерпретацію в термінах теорії надійності технічних виробів і пристроїв. Воно означає, що інтенсивність відмов (тобто інтенсивність виходу виробів з ладу) є постійною, інакше кажучи, не залежить від того, скільки часу виріб уже проробив. Звичайно інтенсивність відмов постійна на основному етапі експлуатації, після того, як на початковому етапі виявлені приховані дефекти, і до того, як через природне старіння матеріалів починає відбуватися прискорене зношування з різким зростанням інтенсивності виходу виробів з ладу.

Показниковий розподіл є однопараметричним: його щільність (12) і інтегральна функція залежать від одного параметра .

Цей закон характерний для розподілу випадкових величин, зміну яких обумовлено впливом якогось домінуючого фактора. За показниковим законом розподілено інтервал між однотипними випадковими подіями: викликами на АТС, замовленнями до фірми, страховими випадками. Він використовується також при розгляді термінових відмов деталей у тих випадках, коли явища зношування і утоми виражені настільки слабко, що ними можна зневажити (наприклад, наробіток до відмови багатьох не відновлюваних виробів). Показниковий закон застосовують для опису часу обслуговування заявок у теорії масового обслуговування.

Характеристики експоненціального розподілу такі: математичне сподівання , дисперсія , асиметрія , ексцес . Помітимо, що характерною рисою цього закону є рівність математичного сподівання і середнього квадратичного відхилення: .

Експоненціальний розподіл є частковим випадком розподілу Вейбула–Гнеденка.