1.4.4. Критерій в.І.Романовського

Для цього критерію так само, як і для критерію узгодження Пірсона, необхідно обчислювати величину статистики, за допомогою якої розраховують значення

. (25)

Тут визначає число степенів вільності розподілу, – число груп або часткових інтервалів статистичного розподілу, – кількість параметрів теоретичного закону, знайдених по ЕД. Нагадаємо, що статистику обчислюють за формулою (21) і перевіряють правильність проведених обчислень за допомогою співвідношення .

Відповідно до критерію Романовського:

• якщо , то можна стверджувати, що статистичний розподіл підпорядковано даному закону розподілу і отримана розбіжність між теоретичними і емпіричними частотами є випадковою за рахунок обмеженого об'єму вибірки;

• якщо , то розбіжності між теоретичними і емпіричними частотами не є випадковими, а свідчать про наявність істотної різниці між статистичним і теоретичним законами розподілу.

Приклад 9. Перевірка гіпотези про нормальний розподіл ЕД за критерієм узгодження Романовського

У прикладі 4 побудовано теоретичні частоти в припущенні розподілу ЕД за нормальним законом. Перевірити узгодженість теоретичних і емпіричних частот за критерієм Романовського.

	2	12	44	92	38	11	1
	1	12	51	79	46	10	1

Розв'язання: проведемо необхідні для визначення –статистики обчислення в табл.11.

Таблиця 11

Розрахунок –статистики

2	1	1	1	4	4
12	12	0	0	144	12
44	51	49	0,96	1936	37,96
92	79	169	2,14	8464	107,14
38	46	64	1,39	1444	31,39
11	10	1	0,1	121	12,1
1	1	0	0	1	1
			5,59		205,59

Перевірка доводить правильність проведених обчислень

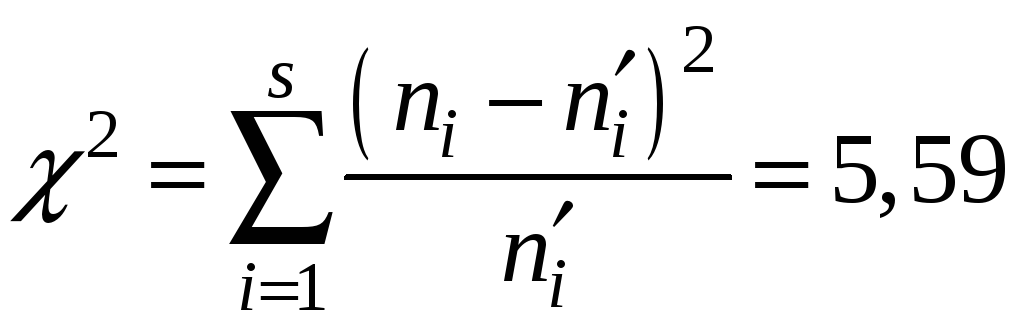
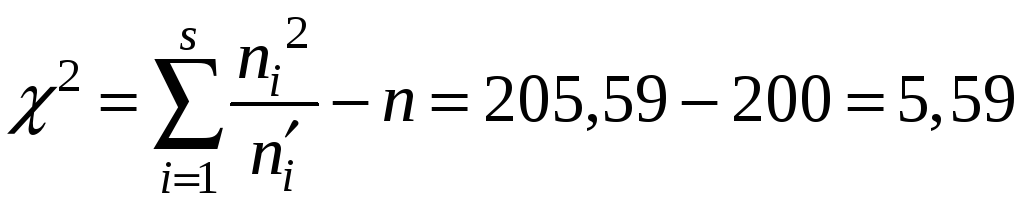
Нормальний закон є двохпараметричним (по ЕД визначають два параметри і ), тому . Число інтервалів статистичного ряду , тому . За формулою (25) знаходимо статистику критерію узгодження Романовського

.

Оскільки , то немає підстав відхилити гіпотезу про те, що час обробки деталей розподілено за нормальним законом.