
- •Предисловие
- •Глава I
- •§ 1. Предмет методики преподавания математики
- •§ 2. Цели обучения математике в советской средней общеобразовательной школе. Значение школьного курса математики в общем образовании
- •§ 3. Содержание школьного курса математики
- •§ 4. Вопросы политехнического образования в обучении математике
- •Литература
- •Глава II
- •§ 1. Принципы обучения как категории дидактики
- •§ 2. Принцип коммунистического воспитания
- •§ 3. Принцип научности
- •§ 4. Принцип сознательности, активности и самостоятельности
- •§ 5. Принцип систематичности и последовательности
- •§ 6. Принцип доступности
- •§ 7. Принцип наглядности
- •§ 8. Принцип индивидуального подхода к учащимся
- •§ 9. Принцип прочности знаний
- •Литература
- •Глава III
- •§ 1. Математические понятия
- •§ 2. Математические предложения
- •2) Рассмотрим определение четной функции:
- •§ 3. Математические доказательства
- •Литература
- •Глава IV методы обучения математике
- •§ 1. Проблема методов обучения
- •§ 2. Эмпирические методы: наблюдение, опыт, измерения
- •§ 3. Сравнение и аналогия
- •§ 4. Обобщение, абстрагирование и конкретизация
- •§ 5. Индукция
- •§ 6. Дедукция
- •§ 7. Анализ и синтез
- •§ 8. Методы проблемного обучения
- •§ 9. Особенности программированного обучения
- •§ 10. Специальные методы обучения математике
- •Литература
- •Глава V
- •§ 1. Значение учебных математических задач
- •§ 2. Роль задач в процессе обучения математике
- •§ 3. Обучение математике через задачи
- •§ 4. Общие методы обучения решению математических задач
- •§ 5. Организация обучения решению математических задач
- •Литература
- •Глава VI организация обучения математике
- •§ 1. Урок, его структура. Основные требования к уроку. Типы уроков
- •§ 2. Подготовка учителя к уроку. Анализ урока
- •§ 3. Организация самостоятельной работы при обучении учащихся математике
- •§ 4. Организация повторения
- •§ 5. Предупреждение неуспеваемости
- •§ 6. Индивидуализация и дифференциация при обучении
- •§ 7. Проверка знаний, умений и навыков учащихся по математике
- •§ 8. Специфика организации обучения математике в школе продленного дня
- •§ 9. Специфика обучения математике в вечерней (сменной) средней общеобразовательной школе
- •§ 10. Особенности организации работы по математике в средних профтехучилищах
- •Литература
- •Глава VII средства обучения математике
- •§ 1. Учебник математики
- •§ 2. Дидактические материалы и справочная математическая литература
- •§ 3. Учебное оборудование по математике и методика использования его в учебной работе
- •§ 4. Организация и оборудование кабинета математики
- •§ 5. Некоторые вопросы изготовления наглядных пособий по математике
- •Литература
- •Глава VIII
- •§ 1. Особенности преподавания математики в школах и классах с углубленным изучением этого предмета
- •§ 2. Факультативные занятия по математике
- •§ 3. Внеклассная и внешкольная работа по математике
- •Литература
§ 7. Анализ и синтез
7.1. Анализ — логический прием, метод исследования, состоящий в том, что изучаемый объект мысленно (или практически ) расчленяется на составные элементы (признаки, свойства, отношения), каждый из которых исследуется в отдельности как часть расчлененного целого.
Синтез — логический прием, с помощью которого отдельные элементы соединяются в целое.
Очень часто умение мыслить связывают с умением анализировать. Это вполне правомерно, так как вывод следствий, выражающих новые свойства изучаемого объекта, очень часто требует анализа того, что уже известно о нем.
В математике, чаще всего, под анализом понимают рассуждение в «обратном направлении», т. е. от неизвестного, от того, что необходимо найти, к известному, к тому, что уже найдено или дано, от того, что необходимо доказать, к тому, что уже доказано или принято за истинное.
В таком понимании, наиболее важном для обучения, анализ является средством поиска решения, доказательства, хотя в большинстве случаев сам по себе решением, доказательством еще не является.
Синтез, опираясь на данные, полученные в ходе анализа, дает решение задачи или доказательство теоремы.
Мы ограничимся этим пониманием анализа и синтеза.
7.2. Анализ лежит в основе весьма общего подхода к решению задач (имеется в виду нестандартных задач, для которых нет соответствующего алгоритма), известного под названием сведения (редукции) задачи к совокупности подзадач.
Идея такого подхода состоит именно в свойственном для анализа «размышлении в обратном направлении» от задачи, которую предстоит решить, к подзадачам, затем от этих подзадач к подподзадачам и т. д., пока исходная задача не будет сведена к набору элементарных задач. Что же понимают под «элементарными задачами»? Это, во-первых, задачи, решаемые за один шаг поиска, во-вторых, более сложные задачи (т. е. не решаемые за один шаг поиска), решение которых уже известно из имеющегося опыта решения задач.
Из такого понимания элементарной задачи следует, что чем больший опыт решения задач, тем больше задач становятся для нас «элементарными» в упомянутом выше смысле, а следовательно, тем меньше объем поиска при решении новых задач, их сведения к элементарным, так как цель поиска состоит в получении элементарных задач, останавливающих процесс поиска.
Рассмотрим пример применения описанного подхода к решению задачи на доказательство: «Если через точку вне окружности провести секущую и касательную, то произведение секущей на ее внешнюю часть равно квадрату касательной».
Обозначим для
краткости через Р условие:
![]() —
касательная,
—
касательная,
С — точка касания;
![]() —
секущая,—
—
секущая,—
![]() ее внешняя часть;
ее внешняя часть;
через Q
— заключение:
![]() (рис.
20).
(рис.
20).
Во введенных обозначениях задача запишется так:
![]()
гДе Г — совокупность уже известных истинных предложений геометрии.
Доказываемое равенство непосредственно из ранее известного получить как будто нельзя. Нельзя ли это равенство несколько преобразовать? Его можно представить в виде пропорции
![]()
С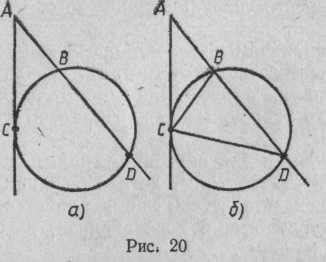 ледовательно,
ледовательно,
![]() , Q-элементарная
задача.
, Q-элементарная
задача.
Но тогда возникает новая задача:
![]()
Откуда можно
получить пропорциональность отрезков?
Очевидно, из подобия треугольников, в
которых эти отрезки являются
сходственными сторонами. Какие же
треугольники нужно образовать? Это
видно из самой пропорции. Если члены
первого отношения
![]() будем считать сторонами одного
треугольника, а члены второго отношения
будем считать сторонами одного
треугольника, а члены второго отношения
![]() —
сторонами другого треугольника,
—
сторонами другого треугольника,
то нужно образовать треугольники ACD и ABC, т. е. соединить точки (С, D) и (В, С) (рис. 20, б) (к этому же мы придем, если допустим, что предыдущие члены отношений — стороны одного треугольника, а последующие — стороны другого).
Итак,— элементарная задача (пропорциональность сходственных сторон непосредственно следует из подобия треугольников), но тогда возникает новая задача:
![]()
Перебирая (в уме) признаки подобия треугольников и учитывая, что пропорциональность сторон нам нужно доказать и поэтому на нее нельзя ссылаться, приходим к элементарной задаче:
![]() (первый признак
подобия треугольников). Но тогда возникают
еще две новые задачи:
(первый признак
подобия треугольников). Но тогда возникают
еще две новые задачи:
![]()
первая из которых тривиальна (совпадающие углы равны), вторая непосредственно следует из измерения вписанного угла и угла, образованного касательной и хордой, и поэтому может считаться элементарной.
На этом сведение исходной задачи к подзадачам завершается.
Теперь, идя обратным путем, от элементарных задач, к которым мы свели в конце концов исходную задачу, мы получим решение этой задачи, т. е. доказательство сформулированного предложения.
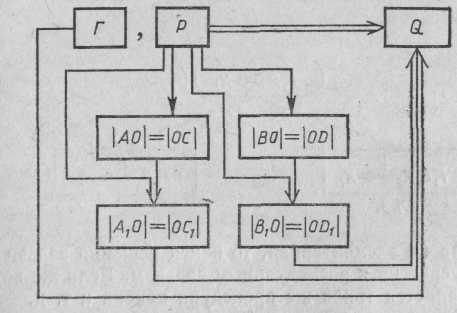
Осуществленный поиск (с помощью сведения задачи к совокупности подзадач) доказательства и само полученное в результате этого поиска решение могут быть наглядно представлены в виде следующих графов:
В приведенном примере исходная задача была сведена к одной совокупности подзадач, в результате чего был открыт один способ решения (доказательства). Однако часто подобный поиск открывает возможность сведения исходной задачи к альтернативным совокупностям подзадач. Такой процесс сведения наглядно изображается с помощью так называемого И/ИЛИ графа.
Изображенный на рисунке 21 с помощью такого графа процесс сведения задачи А состоит в следующем: для решения задачи А достаточно решить одну из задач В или С (В и С называются ИЛИ- вершинами графа или вершинами типа ИЛИ). Для решения задачи В необходимо решить задачи D и Е (D и Е называются И- вершинами


или вершинами типа И). Такого же типа являются вершины F, G Н, К, L (стрелки, ведущие к И- вершинам, соединены дугой). Вершины же М и Р являются опять ИЛИ-вершинами (для решения задачи Я достаточно решить одну из задач — М или Р).
И/ИЛИ-граф оказывается подходящей формой для наглядного представления процесса сведения и может быть использован в обучении.
Приведем пример.
Задача. Доказать, что середины полудиагоналей параллелограмма являются вершинами параллелограмма.
Обозначим через
Р совокупность посылок (условие),
т. е.
![]() параллелограмм;
параллелограмм;
![]() (рис. 22).
(рис. 22).
1режде чем приступить к поиску решения сведением задачи к подзадачам, необходимо вспомнить все связанные с рассматриваемыми в задаче объектами уже известные положения (определения, признаки, другие ранее доказанные теоремы, касающиеся параллелограмма, треугольника, средней линии треугольника). Эти положения могут оказаться полезными в процессе сведения данной задачи к подзадачам.
Определение и каждый из известных признаков параллелограмма подсказывает возможное направление поиска. Можно вести поиск по всем этим направлениям, если мы хотим найти различные способы доказательства. Но, если мы ищем один, возможно более простой, способ, мы ведем поиск лишь в том направлении, которое кажется более перспективным, исходя из той эвристической информации, которая заложена в условии. Так как условие связано с диагоналями, то можно предполагать, что именно признак параллелограмма, связанный со свойствами диагоналей, быстрее приведет к цели.
На приведенном
ниже фрагменте и/или-графа поиск доведен
до конца лишь в этом направлении, на нем
для краткости через Q
обозначено заключение («![]() —
параллелограмм»).
—
параллелограмм»).
П олный
граф поиска (по всем направлениям)
позволяет сравнить различные способы
доказательства, выявить наиболее
рациональный (приведенный на схеме) и
подсказывает учителю, как направить
поиск учащихся по кратчайшему пути.
олный
граф поиска (по всем направлениям)
позволяет сравнить различные способы
доказательства, выявить наиболее
рациональный (приведенный на схеме) и
подсказывает учителю, как направить
поиск учащихся по кратчайшему пути.
Как показывает этот пример, из условия задачи можно извлечь эвристическую информацию, способствующую открытию наиболее перспективного направления поиска.
Найденный способ доказательства может быть представлен . в виде следующего графа, наглядно изображающего синтез этого доказательства и легко получающегося из графа поиска, если продвигаться от элементарных задач к началу, т. е. к доказываемому предложению.
7.3. Внимательно изучив оба примера сведения задачи на доказательство к подзадачам, можно заметить, что в них применена одна И та же схема поиска доказательства. Ввиду того что эта схема встречается довольно часто, рассмотрим ее в общем виде.
Пусть необходимо доказать предложение
![]()
Мы уже знаем, что эту задачу можно представить в виде
![]()
где Г — совокупность уже известных предложений теории, на языке которой сформулировано и доказываемое предложение.
Общая схема сведения к подзадачам задач такого вида состоит в том, что в исходную задачу вводят новые дополнительные посылки так, чтобы получить элементарную задачу, а затем формулируют дополнительные задачи на доказательство этих новых посылок.
Так, при, сведении задачи (1) может быть добавлена одна новая посылка X1. В этом случае получаем:

Если задача (2) элементарная, то процесс сведения задачи (1) к элементарным задачам завершен.
Если же задача (2) не является элементарной, то к ней применяется такая же процедура поиска, что и к задаче (1), т. е. ищем такую посылку Х2, добавление которой позволило бы нам получить элементарную задачу и новую задачу на доказательство дополнительной посылки Х2:

Если задача (3) элементарная, то поиск решения задачи (1) заканчивается, она сведена к элементарным задачам. Если же нет, то к задаче (3) применяется такая же процедура поиска и т. д.
Но что здесь означает «и т. д.»?
Процесс поиска должен быть конечен и состоять из не очень большого числа, шагов, так как его осуществляет человек. Очень большой объем поиска часто является причиной того, что процесс решения не доводится до конца.
Вообще, процесс поиска (по описанной выше схеме) может иметь два исхода: либо через определенное число шагов мы получаем элементарные задачи (т. е. поиск привел к решению исходной задачи), либо на каком-то шагу мы получаем неэлементарную задачу, которую не удается свести к элементарным таким же путем, т. е. в наших знаниях мы не находим той дополнительной посылки, с помощью которой
это можно было бы сделать. В таком случае поиск не привел к решению исходной задачи, нас постигла неудача, или, как часто говорят, «мы зашли в тупик». Если это случилось, то необходимо (возможно после некоторого перерыва) возобновить поиск решения задачи, но уже по другому направлению, с помощью других «операторов сведения»!
О![]() писанная
схема поиска не всегда применяется в
таком виде, когда на каждом шагу
добавляется только одна дополнительная
посылка.
писанная
схема поиска не всегда применяется в
таком виде, когда на каждом шагу
добавляется только одна дополнительная
посылка.
Встречаются случаи, как это имело место в одном из приведенных примеров, когда одновременно добавляется несколько дополнительных посылок, чтобы превратить нашу задачу в элементарную, и получают несколько новых задач на доказательство этих дополнительных посылок:

Иногда, как это случилось во втором из приведенных примеров, в самом начале поиска доказательства мы обнаруживаем несколько возможных направлений поиска и ведем его по всем этим направлениям, открывая различные способы доказательства.
Описанная схема поиска доказательства, естественно, не единственно возможная. Она также не является универсальной, т. е. применимой к любой задаче на доказательство, независимо от структуры доказываемого предложения.
7.4. Подход к решению задач, состоящий в сведении задач к совокупности подзадач, находит широкое применение в практике решения не только задач на доказательство.
Приведем в качестве примера арифметическую задачу для IV класса: «В двух бригадах совхоза участки под зерновые составляли 2000 га и 3000 га соответственно. Первая бригада собрала по 30 ц, вторая rjo 26 ц с гектара. Продано государству 5500 т е первого участка и 7000 т со второго. Остальное зерно засыпано в семенной фонд. Сколько зерна засыпал совхоз в семенной фонд?»
О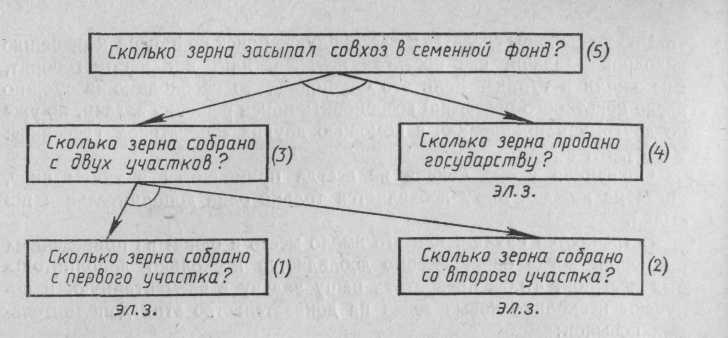 бычно
анализ задачи по существу представляет
собой процесс сведения данной задачи
к совокупности подзадач, доведенный до
элементарных задач. Здесь элементарной
считается задача, решаемая с помощью
не более одного действия над данными
задачи (т. е. элементарной считается
и задача, решение которой находится
среди данных, например: «Сколько
зерна продано государству с первого
участка?»).
бычно
анализ задачи по существу представляет
собой процесс сведения данной задачи
к совокупности подзадач, доведенный до
элементарных задач. Здесь элементарной
считается задача, решаемая с помощью
не более одного действия над данными
задачи (т. е. элементарной считается
и задача, решение которой находится
среди данных, например: «Сколько
зерна продано государству с первого
участка?»).
Возможен и иной путь поиска.
Построение самого процесса решения (синтез) осуществляется последовательным решением подзадач в обратном порядке, начиная с элементарных (1—2—3—4—5).
