2.3. Условия применения линейных моделей при описании функционирования производственных систем

После описания ряда конкретных моделей и их обобщения в основной планово-производственной задаче Канторовича целесообразно рассмотреть некоторые теоретические проблемы описания функционирования производственных систем.

Известно, что для описания процесса функционирования производственной системы используется метод производственных функций.

Пусть, как и выше в процессе производства система использует т видов ресурсов и пусть вектор характеризует данный набор используемых ресурсов. В свою очередь, производственная система включает определенный набор технологических способов производства: Т₁,..., Т_r , при этом по s-му способу выпускается продукция s-го наименования, в производстве которой используются все виды ресурсов или только некоторая их часть. Производственная функция связывает объем потребляемых по s-й технологии ресурсов с величиной выпуска валовой (в натуральных единицах) или товарной (в стоимостном выражении) продукции s-го наименования.

Таким образом, где х_s — объем продукции, выпускаемой по s-й технологии, f_s — соответствующая производственная функция (ПФ).

Если математическая сущность ПФ заключается в том, что она задает отображение множества наборов ресурсов на множество товарных выпусков , то экономическая сущность ПФ заключается в том, что соотношение выражает объем продукции, выпущенной по s-й технологии, при наиболее рациональном использовании ресурсов. Основной целью функционирования системы управления производством является выбор вектора ресурсов , а также способа реализации технологии Т_s , при котором будет реализован “оптимальный” способ использования ресурсов.

Производственная функция является одним из основных инструментов планово-производственных расчетов при анализе производственно-коммерческой деятельности промышленной фирмы. Как будет ясно из дальнейшего, ПФ объектов микроэкономики могут быть как линейными, так и (очень часто) нелинейными.

Рассмотрим очень важный для модельных приложений случай, когда технологическое множество производственной системы является линейным выпуклым множеством. В этом случае модель производства оказывается линейной.

Основная предпосылка возможного применения этой модели состоит в том, что любой происходящий производственный процесс можно представить в виде линейной комбинации с неотрицательными коэффициентами некоторых основных (или базовых) производственных процессов. В свою очередь, каждый из этих процессов задается при помощи вектора “выпуск-затраты”, размерность которого определяется суммой количества видов производимых продуктов и потребляемых ресурсов. Коэффициенты в разложении данного производственного процесса по базовым производственным процессам назовем, как и выше, интенсивностями основных способов.

Одним из примеров, характеризующих сказанное, является интерпретация основного производственного способа как производства продукции и расхода ресурсов в единицу времени. В этом случае величины интенсивностей выражают собой, например, количество смен работы некоторого производственного участка по какой-либо из r технологий. В этом случае основные показатели выпуска продукции и затрат ресурсов на всем производстве являются суммой выпусков и затрат отдельных участков. Последнее и служит основой для представления модели производства как линейной.

Дадим теперь строгие предположения относительно множества технологий Т₁,..., Т_r , которые приводят к линейным моделям.

Предположение 2.1 (об однородности технологических способов или закон постоянства удельного выпуска независимо от масштаба производства):

если то для всякого    справедливо

Это предположение означает, что если технологически допустимым является вектор то технологически допустимы также векторы “выпуск-затраты”, у которых выпуск увеличивается (уменьшается) в  раз при одновременном увеличении (уменьшении) затрат также в  раз.

Предположение 2.2 (об аддитивности технологических способов):

если а то существует такая технология Т, для которой

Это предположение означает, что, если возможен выпуск продукции s₁-го наименования в количестве при затратах вектора ресурсов , а также выпуск продукции s₂-го наименования в количестве при затратах вектора ресурсов , то допустимым является выпуск вектора + при затратах ресурсов +.

Предположение 2.3 (о линейной структуре множества технологий):

существует конечное число основных технологических способов (каждый из которых является вектором “выпуск-затраты”): Р₁,..., Р_К таких, что для любого технологически допустимого набора найдутся такие неотрицательные числа ₁,..., _К , что справедливо соотношение

Замечание. Совместно предположения 2.1 и 2.2 означают, что технологическое множество является выпуклым конусом. Предположение 2.3, выделяющее линейные технологии, означает, что этот конус является выпуклым многогранником в полупространстве .

Таким образом, в качестве основного параметра линейной производственной системы можно принять вектор основных производственных способов Р₁,..., Р_К . При этом характеристикой внутреннего состояния системы следует считать неотрицательный вектор их интенсивностей . Вектор , описывающий функционирование всего производства, имеет вид

При помощи ограничений на компоненты вектора формируются производственные и ресурсные ограничения на множества допустимых значений интенсивностей основных технологических процессов. Кроме того, каждая производственная система обладает специфическими ограничениями на интенсивности отдельных технологических способов, обусловленными особенностями производства.

На множестве возможных состояний формируется некоторое правило выбора наилучшего или оптимального состояния производственной системы. Наиболее часто это правило имеет содержательный смысл выпуска наибольшего количества продукции, максимального увеличения прибыли или минимизации затрат. Иногда это правило формулируется путем постановки задачи многоцелевой оптимизации.

Итак, мы рассмотрели связи, существующие между производственными функциями и основной планово-производственной задачей Канторовича, являющейся обобщением линейных оптимизационных задач. Не случайно наиболее общие из встречающихся в литературе многочисленных определений производственной функции не противоречат по своей сути содержанию оптимизационных задач, а определение множества производственных возможностей, как множества всех возможных сочетаний затрат и выпусков, корреспондирует с определением области допустимых планов. При этом мы оставались в рамках наиболее простого с математической стороны случая линейности всех исследуемых зависимостей, т.е. в рамках предпосылки о пропорциональности затрат выпускам и наоборот.

Представим себе любую линейную оптимизационную задачу и кратко напомним основные особенности симплекс-метода. Его идея состоит в переходе от одного базисного (опорного) плана к другому таким образом, что линейная форма улучшается на каждом шаге и достигает экстремума. Переход происходит по вершинам выпуклого многогранника условий в n-мерном пространстве, причем на каждом шаге переход осуществляется в соседнюю вершину. При нахождении в такой вершине проводится проверка плана на оптимальность. Линейная форма (гиперплоскость) делит всё пространство на две части. Вершинам, находящимся в верхней части, соответствуют отрицательные элементы целевой строки, а вершинам из нижней части — положительные. Переход осуществляется только в соседние вершины из верхнего полупространства до тех пор пока в нем не останется ни одной вершины. Переход проводится в ту вершину, которой соответствует максимальный по абсолютной величине из отрицательных элементов целевой строки. Если на последнем шаге линейная форма имеет более одной общей точки с выпуклым многогранником условий, то имеется множество оптимальных планов. Итак, отличительной особенностью метода является движение к оптимуму по вершинам. Все отмеченные выше особенности можно проследить на рис.2.1, где представлен многогранник условий ОАВСD и показаны положения линейной формы при последовательном движении по вершинам О, А и В (точка оптимума).

На данном рисунке хорошо видно, что для задач линейного программирования характерно следующее:

x₂

А

В

С

О D x₁

Рис 2.1

1.Множество допустимых решений выпукло и имеет конечное число крайних точек (вершин);

2.Целевая функция представляет собой гиперплоскость. Гиперплоскости, соответствующие разным значениям целевой функции параллельны.

3.Локальный оптимум является одновременно и глобальным оптимумом.

4.Если целевая функция ограничена на множестве допустимых решений, то оптимум достигается по крайней мере в одной из крайних точек вершин) этого множества, и, начав с произвольной вершины, перемещаясь затем на каждом шаге в соседнюю, достигаем точки оптимума за конечное число шагов.

В задачах нелинейного программирования эти условия полностью или частично не соблюдаются. Рассмотрим ряд случаев.

Случай 1. Пусть при линейных ограничениях имеем нелинейную, сепарабельную целевую функцию вида

с₁ (x₁- x₁) ² + с₂ (x₂- x₂) ²  min ,

которая экономически представляет собой штраф за отклонение нашего решения от рекомендованного (желательного). Причем, благодаря возведению в квадрат, одинаково штрафуются отклонения искомых значений выпусков x₁ и x₂ в любую сторону от их заданных значений x₁ и x₂. Штрафные коэффициенты с₁ и с₂ определяют силу штрафа. Как видим из рис.1.2 , различным значениям целевой функции соответствуют эллипсы с центрами в точке (x₁, x₂), а оптимум достигается в точке А, точке касания эллипсом границы выпуклого множества допустимых

x₂

x₂

А

O x₁

x₁

Рис 2.2

решений.

Итак, в данном случае невыполнение условия 2 влечет за собой и невыполнение условия 4. Оптимум достигается не на вершине, а на грани, откуда следует, что перебор вершин недостаточен.

Из рис. 2.2 видно, что при смягчении заданий по выпуску продукции x₁ и x₂ можно уменьшить сумму штрафа вплоть до нуля. Так, сместив центр эллипса вовнутрь многогранника условий, получим, что оптимум достигается во внутренней точке.

Случай 2. При иной конфигурации области допустимых значений, описываемой как и ранее линейными ограничениями, и при опять-таки нелинейной сепарабельной целевой функции вида

p₁ (x₁- x₁) ² + p₂ (x₂- x₂) ²  max ,

получим рис.2.3. Данная целевая функция экономически представляет собой премию за отклонения выпусков x₁ и x₂ от зара-

x₁

B

E C

A

D x₂

Рис.2.3

нее заданных их значений x₁ и x₂, где значения коэффициентов p₁ и p₂ определят силу таких премий. Как видим из рис.2.3, при расположении центра эллипсов внутри многогранника условий в точке Е с координатами x₁ и x₂ возможно попадание в локальный оптимум в вершине А. Перемещение из нее в соседние вершины В или D ухудшит значение целевой функции (уменьшит эллипс), хотя в вершине С достигается глобальный оптимум. Итак невыполнение условия 2 ведет и к невыполнению условия 3.

Случай 3.Пусть одно из ограничений будут нелинейным, а именно:

(x₁ - a₁) (x₂ - a₂)  b₁ ,

где x₁ и x₂ — искомые выпуски двух видов продукции, a₁ и a₂ — минимально разрешенные (по технологическим или экономическим соображениям) размеры производства, a b₁ — предельно допустимый уровень загрязнения окружающей среды, мультипликативно зависящий от объемов производства двух видов продукции. Кроме того, имеются обычные ограничения по производственной программе и на неотрицательность переменных

x₁ + x₂  b₂ ;

x₁  0 ; x₂  0 .

На рис. 2.4 заштрихована область допустимых решений. Как

x₂

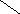
a₂

О a₁ x₁

Рис.2.4

видим, она состоит из двух несвязанных областей. Более того, каждое из двух подмножеств допустимых решений невыпукло. В этих условиях даже линейность целевой функции не может гарантировать от локального оптимума.

Итак, невыполнение условия 1 ведет к невыполнению условий 3 и 4.

Случай 4. Требование целочисленности решения даже при наличии прочих линейных ограничений и линейной целевой функции ведет к невыполнению условий 1 и 4. Из рис.2.5 видно, что область допустимых целочисленных значений переменных состоит из четырех точек О, А, D и Е , а оптимум достигается в точке D. Причем это решение не только существенно хуже оптимального решения без условий целочисленности (достигается в точке В), но и не может быть получено путем его округления до ближайших целых чисел (точки А и С).

x₂

С

B

D

A

O x₁

E

Рис.2.5

Рассмотренные случаи не являются исчерпывающими и служат лишь иллюстрацией, из которой видно, что в чисто вычислительном аспекте для нелинейных задач характерны затруднения с получением точного решения, либо из-за попадания в локальный оптимум, либо из-за плохой сходимости вычислительного процесса. Кроме того, методы нелинейного программирования в отличие от линейного не являются универсальными и приспособлены для решения лишь ограниченного круга задач того или иного специального класса, а потому гораздо более чувствительны к размерности задач.

С содержательной же стороны использование линейных зависимостей дает возможность предельно прозрачно экономически интерпретировать не только модели, отдельные математические выражения и входящие в них величины, а также результаты решения, но даже и сами вычислительные процедуры. Подобные свойства линейных моделей делают их весьма удобными с методической точки зрения для усвоения в процессе обучения общих экономических принципов и закономерностей.

В экономической практике и исследованиях вычислительная привлекательность и хорошая интерпретируемость линейных моделей (не обязательно оптимизационных, т.е. моделей в широком смысле) делает целесообразным их применение и в случае линейной аппроксимации с приемлемой погрешностью нелинейных закономерностей, если это не мешает экономическому содержанию задачи.