12 Перпендикулярность прямой и плоскости.

Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, принадлежащим этой плоскости.

Если прямая перпендикулярна плоскости, то она перпендикулярна любой прямой, принадлежащей этой плоскости. Учитывая свойство прямого угла, этими прямыми должны быть горизонталь, фронталь и профильная прямые. Следовательно, на ортогональном чертеже проекции перпендикуляра к плоскости будут перпендикулярны к соответствующим проекциям горизонтали, фронтали и профильной прямым плоскости или к ее следам (рисунок 72).

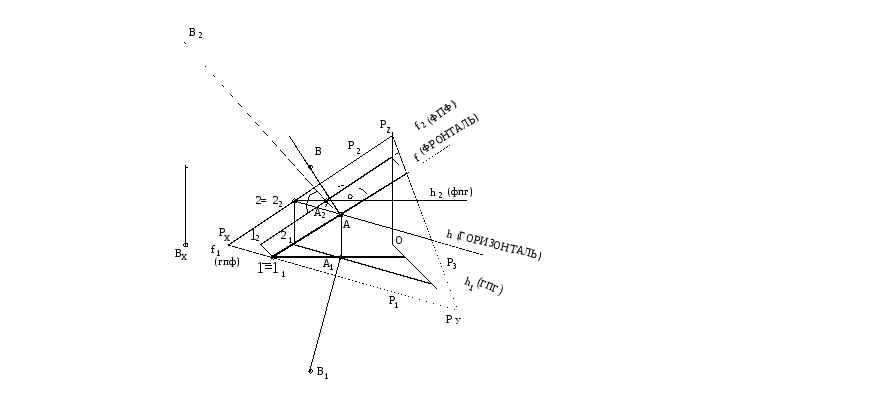
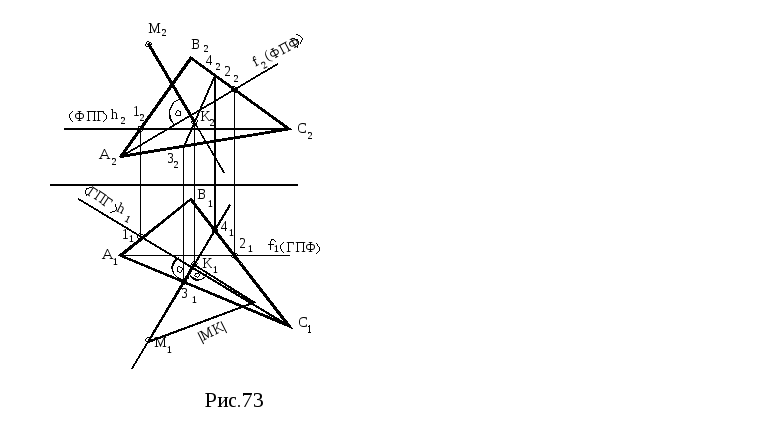
Рисунок 72 Рисунок 73

Пример. Определить расстояние от точки М до плоскости треугольника АВС.

Плоскость треугольника является плоскостью общего положения. Чтобы провести проекции перпендикуляра к плоскости, нужно провести в плоскости линии уровня: горизонталь и фронталь. Тогда горизонтальная проекция перпендикуляра будет перпендикулярна горизонтальной проекции горизонтали, а фронтальная проекция перпендикуляра - перпендикулярна фронтальной проекции фронтали (рисунок 73).

Алгоритм решения задачи:

1. Из точки М опущен перпендикуляр на плоскость АВС

2. Определена точка пересечения перпендикуляра с плоскостью АВС.

3. Определено расстояние от точки М до плоскости АВС, применив метод прямоугольного треугольника.

13 Перпендикулярность плоскостей

Плоскости взаимно перпендикулярны, если одна из них содержит прямую, перпендикулярную к другой плоскости.

Пример. Через точку М провести плоскость, перпендикулярную плоскости треугольника АВС (рисунок 74).

Можно задать плоскость перпендикулярную плоскости треугольника АВС двумя прямыми пересекающимися в точке М. Одна из этих прямых является перпендикуляром к плоскости (прямая МК), а вторая прямая(МЕ) может быть произвольной.

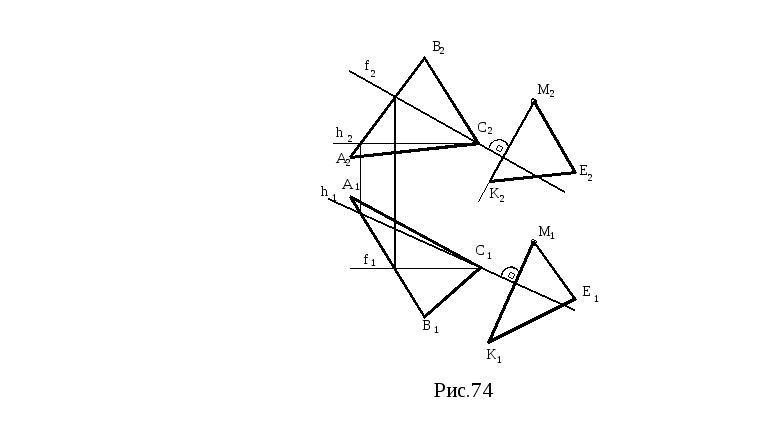
Рисунок 74

14 Методы преобразования чертежа

Методы преобразования чертежа построений, а, следовательно, и точность получаемого ответа часто зависят не от условия задачи, а от расположения заданных геометрических элементов относительно плоскостей проекций. Решение получается более простым и наглядным, если объекты проецирования имеют частное положение относительно плоскостей проекций.

Преобразовать графическую задачу из общего положения в частное можно при помощи методов преобразования чертежа.

14.1 Метод замены плоскостей проекций

Сущность метода замены плоскостей проекций заключается в том, что одна из плоскостей проекций системы П_!/П₂ (или последовательно обе) заменяется новой плоскостью, перпендикулярной к плоскости оставшейся. Положение заданных геометрических элементов в пространстве при этом не изменяется. Образуется новая система плоскостей проекций П₁/П₄ (П₂/П₅).

На рисунке 75 показано проецирование точки на плоскости П₄ и П₅. Плоскость П₄ перпендикулярна плоскости П₁.

[АА₁]=[А₂А_х]=[А₄А_х1],т.е.

расстояние от новой фронтальной проекции до новой оси равно расстоянию от старой фронтальной проекции точки до старой оси.

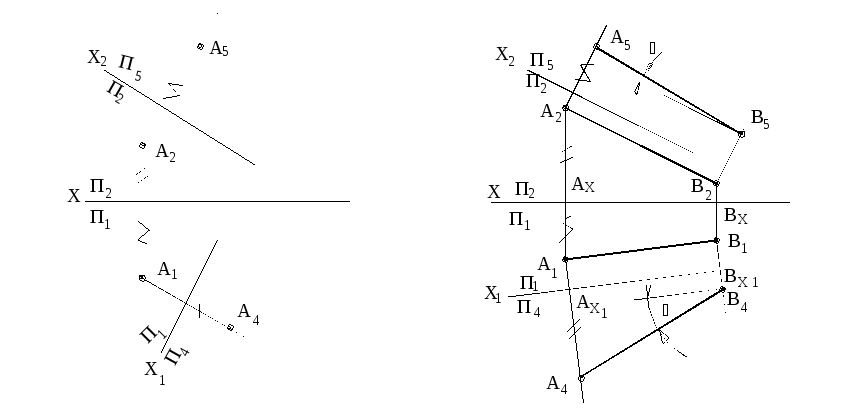
Рисунок 75 Рисунок 76

При построении эпюра в новой системе, новая проекция точки А₄ и старая проекция точки А₁ (или А₅ и А₂ ) расположены на одном перпендикуляре к новой оси.

Пример 1. Определить длину отрезка АВ и угол наклона его к плоскости П₁ и П_2.

Решение задачи показано на рисунке 76.

Введена плоскость П₄ перпендикулярно П₁ и параллельно отрезку АВ, т. к. Х₁ параллелен А₁В₁. А₁А₄ и В₁В₄ находятся на одной линии связи перпендикулярной новой оси Х₁. Отрезки А₂А_х=А₄А_х1; В₂В_х=В₄В_х1. Отрезок[А₄В₄] =[АВ] –длина отрезка.

Углы наклона показаны на чертеже.  - угол наклона к П_1; - угол наклона к П_2.

Для решения некоторых задач требуется вводить поочередно замены двух плоскостей проекций.

Пример 2. Определить истинную величину треугольника АВС.

Последовательность решения задачи на рисунке 77.

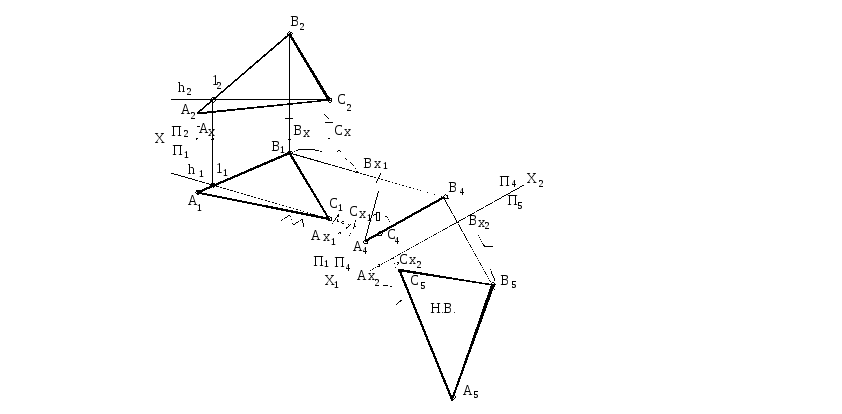
Рисунок 77

1) Введена плоскость П_{4 ┴} П₁; П₂ /П₁ П₄/П₁

Плоскость П₄ перпендикулярна плоскости треугольника АВС, так, как она перпендикулярна горизонтали, проведенной в треугольнике. На плоскости П₄ проекция треугольника А₄В₄С₄- прямая линия, угол - угол наклона плоскости АВС к горизонтальной плоскости проекций П₁.

[А₂А_х]=[А₄А_х1]; [В₂В_х]=[В₄В_х1]; [С₂С_х]=[С₄С_х1].

2) Введена плоскость П_{5 ┴} П₄. П₄/П₁ П₅/П₄

Плоскость треугольника АВС стала параллельна плоскости П₅ т.к. Х₂ параллельна А₄В₄С₄.

[А₁А_х1]=[А₅А_х2]; [В₁В_х1]=[В₅В_х2] ; [С₁С_х1]=[С₅С_х2]

Треугольник А₅В₅С₅-натуральная величина треугольник а АВС.

Пример 3. Определить точку пересечения прямой МЕ с плоскостью общего положения, заданной треугольником АВС.

Последовательность решения задачи на рисунке 78.

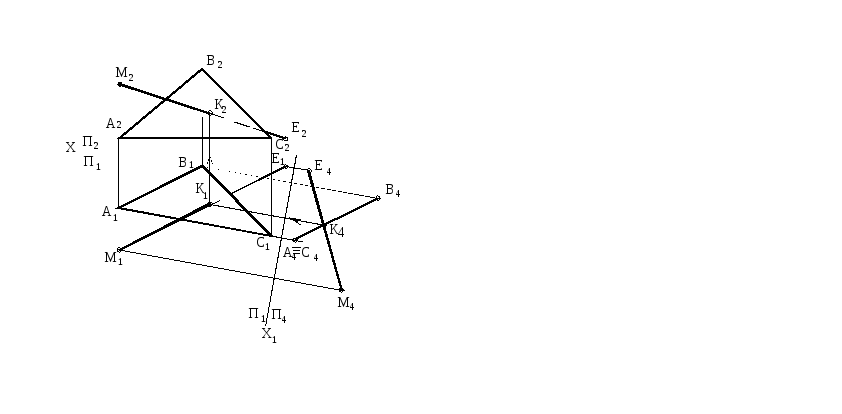
Рисунок 78

Так как прямая ВС является горизонталью, то вспомогательная плоскость П₄ проводится перпендикулярно П₁, а новая ось Х₁ будет перпендикулярна горизонтальной проекции горизонтали В₁С₁. Плоскость АВС станет проецирующей относительно плоскости П₄ и проецируется на нее в прямую линию А₄В₄С₄. Поэтому проекция точки К₄ искомой точки пересечения прямой МЕ с плоскостью АВС будет находиться на проекции А₄В₄С₄ или ее продолжении. Обратный переход от системы П₁/П₄ к исходной системе П₁/П₂ позволяет определить проекции К₁ и К₂ точки пересечения прямой МЕ с плоскостью АВС. Относительная видимость прямой и плоскости определяется методом конкурирующих точек.