Тема 7. Интегральное исчисление.

1. Первообразная, неопределенный интеграл и их свойства

Определение

Пусть функции f(x) и F(x) определены на интервале (a,b). Если функция F(x) имеет производную на (а,b) и для всех выполняется равенство.

(1)

то функция F(x) называется первообразной для функции f(x) на интервале (a,b).

Пример

Теорема 1.1

Пусть F₁(x) и F₂(x) - любые две первообразные для функции f(x) на интервале (a,b). Тогда для всех выполняется равенство

где С - некоторая постоянная. (Без доказательства)

Вывод. Если F(x) - одна из первообразных функций для функции f(x) на интервале (a,b), то любая первообразная Ф(x) для функции f(x) на интервале (а,b) имеет вид

Ф(х)=F(х)+С, где С - некоторая постоянная.

Определение

Совокупность всех первообразных функций для функции f(x) на интервале (а,b), называется неопределенным интегралом от функции f(x) на этом интервале и обозначается

Символ называется знаком интеграла, f(x) – подынтегральная функция.

Таким образом, если F(х) - какая-либо первообразная функции f(x) на интервале (а,b). то пишут

Свойства неопределенного интеграла

Свойство 1.

Свойство 2.

Свойство 3.

Свойство 4.

Свойство 5. Пусть F(x) есть первообразная для функции f(x).

Тогда

2.Таблица основных неопределенных интегралов

1. 

2. 

3. 

4. 

5. 

6. 

7. 

8. ;

9. 

10. 

11. 

12. 

13. 

14. 

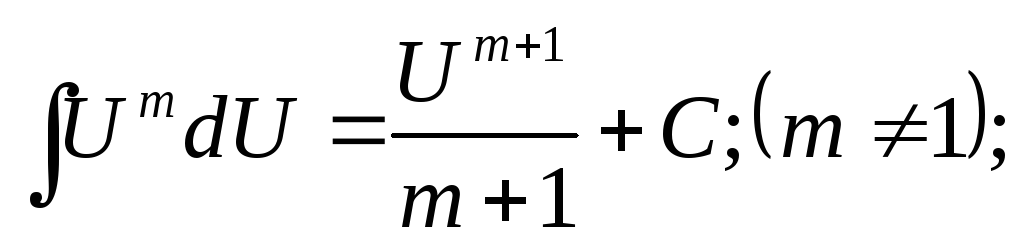
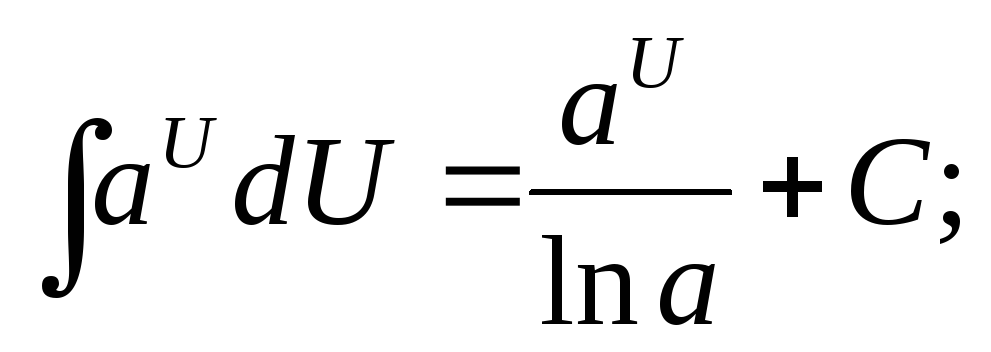
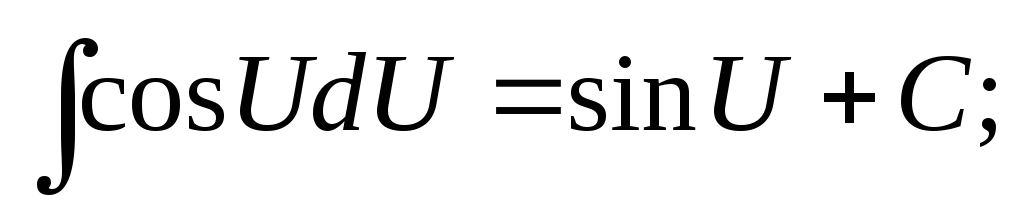
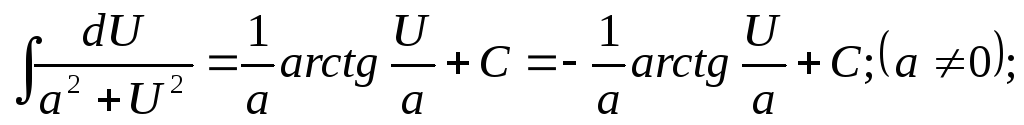
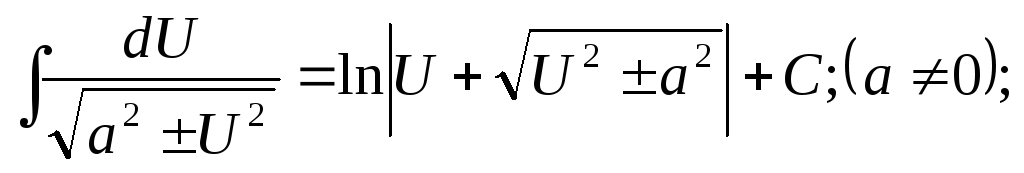
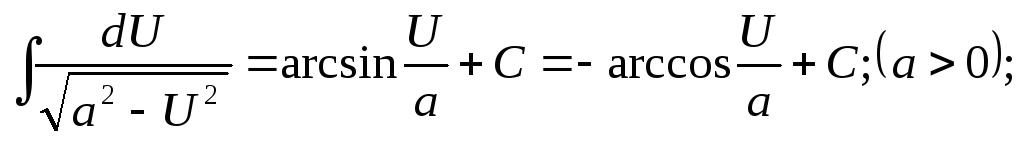
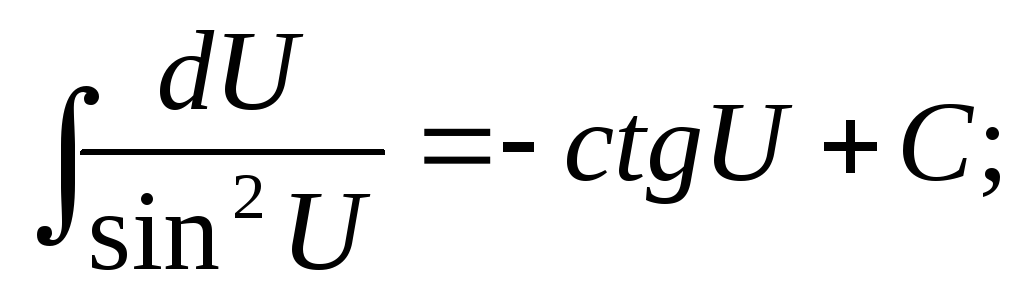
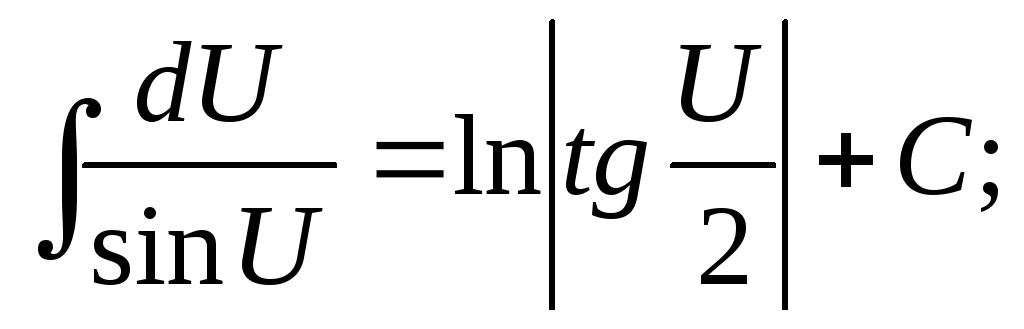
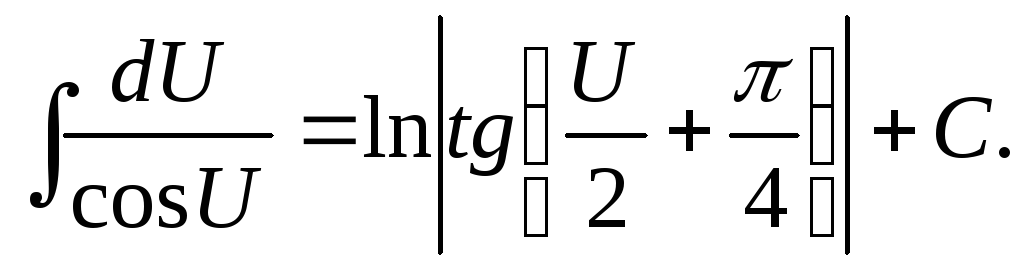
Пример1. Найти неопределенный интеграл

Пример 2. Найти . Это интеграл вида . По свойству 5 неопределенных интегралов имеем

Пример 3. Найти .

Воспользуемся формулами тригонометрии. Отсюда

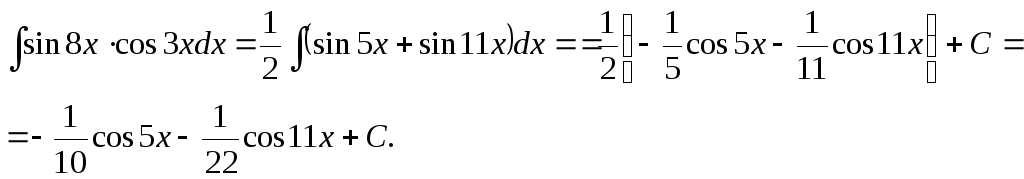
3. Основные методы интегрирования

1). Интегрирование путем подведения под знак дифференциала

На основании свойств неопределенного интеграла имеем

(1)

где F(U) есть первообразная функции f(U).

Пример 1. Рассмотрим интеграл

Известно, что отсюда

Значит, наш интеграл преобразуется следующим образом:

Пример 2. Найти

2). Интегрирование по частям

Теорема 2.1

Если функции U(x) и V(x) дифференцируемы на интервале (а,b), то

(2)

(без доказательства).

Таким образом, вычисление сводится к вычислению , которое может оказаться более простым.

Пример 1. Вычислить .

Положим U=x, , тогда Константу С при определении функции мы опускаем, так как она входит в окончательный ответ dU=dx. Отсюда по формуле (2) имеем

Пример 2. Вычислить интеграл

Пусть U=х, dV=sinxdx, тогда dU=dx, Применим к исходному интегралу формулу интегрирования по частям

Метод интегрирования по частям применяют при вычислении следующих интегралов:

1)

где P_n(x) – полином степени n

В этих интегралах за U(x) принимается P_n(x) и интегрируют по частям n раз.

Пример 3. Применим рассмотренный метод для вычисления интеграла Примем тогда

Окончательно получаем

2)

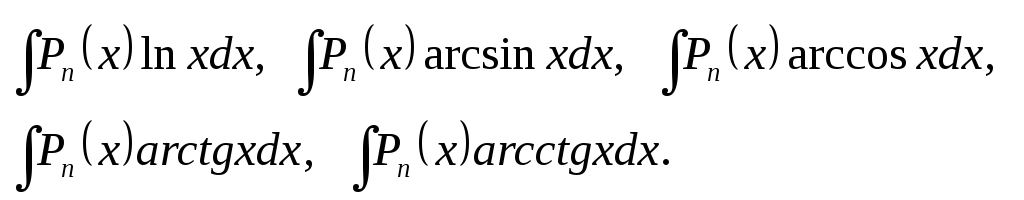
В этих интегралах dV принимается

Пример 4. Вычистить по частям интеграл Сделаем предварительные преобразования, тогда

отсюда

3) .

В этих интегралах, выбор U(x) произволен. Дважды интегрируем по частям. Оба раза за U берем одно и то же. Интеграл сводится к самому себе.

Пример 5. Так в интеграле , примем .

Используя формулу интегрирования по частям (2), имеем

.

Ко второму интегралу повторно применим формулу (2), положив .

Тогда и

Таким образом наш интеграл свелся к самому себе. Разрешим последнее соотношение относительно J₆

или

Замечание. В рассмотренном примере в ответе следовало бы писать константу С₁, так как С₁=4/29 С. Однако константы С и С₁ являются произвольными постоянными величинами, поэтому мы не будем вводить дополнительные индексы. Конечно, указанные группы интегралов не исчерпывают всех, которые можно вычислять по формуле (2).