1 Способ.

1. Рассчитывается значение предполагаемой прибыли в условиях уверенности

2. Рассчитывается значение предполагаемой прибыли в условиях риска

3. Из первого значения вычитается второе

Предполагаемая стоимость точной информации

=

Предполагаемая прибыль в условиях уверенности

-

Предполагаемая прибыль в условиях риска

Формула 1

2 Способ.

Использовать для расчёта EVPI таблицу упущенных возможностей. Чтобы это сделать, необходимо определить предполагаемый убыток для каждой альтернативы. Минимальное значение будет равно

EVPI.

Пример

Используя данные расчёта критерия EMV , определить ожидаемую стоимость точной информации по формуле 1.

Решение

1. Подсчитываем прибыль в условиях уверенности. Для этого определяем максимальную прибыль для каждого из возможных условий. Затем делаем поправку на коэффициент вероятности каждого условия и складываем полученные значения.

2. Так максимальная прибыль в условиях низкого спроса равна 10, при среднем спросе - 12, при высоком спросе - 16

3. Тогда ожидаемая прибыль в условиях уверенности составляет:

4. 0,30 (10)+0,50(12)+0,20 (16)=12,2

5. Ожидаемая прибыль в условиях риска из примера составляет 10,5. Разница между этими двумя величинами

EVPI = 12,2 - 10,5=1,7

Эта цифра показывает верхнюю границу суммы, которую принимающий решение захочет потратить на получение точной информации в данном случае.

Так, если затраты равны, или превышают эту сумму, то целесообразно не тратить эту дополнительные средства, а просто придерживаться альтернативы с максимальной ожидаемой прибылью

Пример

Определить ожидаемую стоимость точной информации для проблемы планирования производственных мощностей с точки зрения убытков от упущенных возможностей.

Решение

Используя информацию из вышеприведённых примеров, можно подсчитать убытки для каждого альтернативного варианта.

Малая мощность	0,30 (0)	+	0,50 (2)	+	0,20(6)	=	2,2
Средняя мощность	0,30 (3)	+	0,50 (0)	+	0,20(4)	=	1,7
Высокая мощность	0,30 (14)	+	0,50 (10)	+	0,20(0)	=	2,2

Наименьший возможный убыток - 1,7, во втором варианте. Следовательно, EVPI =1,7; что согласуется с предыдущим примером.

9. Анализ чувствительности

Можно сказать, что и прибыли, и вероятности в такого рода проблемах часто являются результатами субъективной оценки того, кто принимает это решение. Следовательно , достаточно важно будет использовать показатель, который будет характеризовать чувствительность выбора альтернатив к изменениям этих факторов. Недостатком этого метода является невозможность учесть все возможные комбинации всех переменных. Мы будем говорить об анализе чувствительности показателей вероятности.

Анализ чувствительности - определение такого уровня вероятности, для которого альтернатива имеет максимальную предполагаемую прибыль.

Анализ чувствительности определяет уровень вероятности, за которым выбор варианта не меняется.

Этот подход наиболее полезен, когда имеется два варианта условий. Он предусматривает построение графика, а затем использование алгебраических методов для определения уровня вероятностей, для которых данное решение является оптимальным. График визуально отображает уровень вероятности, для которого различные альтернативные варианты являются оптимальными, а алгебраический расчёт обеспечивает точные координаты конечных точек этих уровней.

Пример

Используя приведённую таблицу, определите тот уровень вероятности для условия №2, т.е. Р(2), для которого каждая альтернатива является оптимальной, используя подход ожидаемой стоимости.

Альтернатива	Возможное условие
	№1	№2
А	4	12
В	16	2
С	12	8

Решение

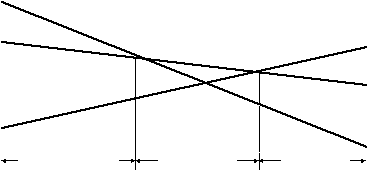
1. Строим на графике все альтернативные варианты связанные с Р (2)

Для этого на левой стороне графика обозначаем показатели №1, а справа - показатели №2

16	В	16
14	А	14
12	С	12
10		10
8		8
6		6
4		4
2	Лучший вариант В Лучший вариант С Лучший вариант А	2

На графике видно, что уровень значений Р (2), сверх которых каждая альтернатива будет оптимальна. Так, для низких показателей Р (2) (следовательно, для высоких показателей Р (1), так как Р(1) + Р(2) = 1,0), альтернатива В будет иметь самую высокую ожидаемую стоимость. Для более высоких оценок Р (2)оптимальна альтернатива А.

Чтобы найти точные значения уровней, определите точки пересечения верхних частей линий. Обратите внимание, что в точках пересечения две альтернативы, представленные данными линиями, будут эквивалентны с точки зрения ожидаемой стоимости. То есть здесь выбор будет равнозначен. Чтобы получить координаты точек пересечения, надо получить уравнения прямых. Уравнение будет иметь вид:

y=a+bx, где

а - точка пересечения с осью у слева, а b - наклон прямой, х - это Р(2) наклон определяется как изменение У при изменении Х на одну единицу. В данных задачах расстояние между осями составляет 1,0. Следовательно, наклон всех прямых равен правому значению минус левое знаяение.

Альтернатива	Возможное условие
	№1	№2	Наклон	уравнение
А	4	12	12 - 4 = +8	У = 4+8 Р(2)
В	16	2	2 - 16 = -14	У = 16 - 14 Р(2)
С	12	8	8 - 12 = - 4	У = 12 - 4 Р(2)

На графике видно, что альтернатива В является оптимальной от Р(2)= 0 до точки, где эта альтернатива пересекает прямую альтернативы С. здесь начинается область, где вариант С лучше. Чтобы найти эту точку, необходимо решить сравнение для альтернативы Р(2) в точках пересечений. Для этого необходимо приравнять оба равенства и решить их для Р(2).

Т.о.

16 - 14 Р(2) = 12 - 4 Р(2) в результате преобразований получаем : 4 = 10 Р(2) решив уравнение, получим Р(2) = 0,40. То есть альтернатива В является лучшей от Р(2) = 0 до Р(2) = 0,40

альтернатива С является наилучшей от этой точки до того момента, когда её прямая пересекает линию альтернативы А. Чтобы найти точку пересечения, приравниваем 4+8 Р(2) = 12 - 4 Р(2). Получаем Р(2) = 0,67. Для оценок от 0,67 и до единицы наилучшим является альтернативы А.

Для определения уровней относительно альтернативы Р (1), определяются уровни дл Р (2 как описано выше, а затем из единицы вычитаются каждое значение Р (2). 0,40 - 0, 60; 0, 67 - 0,33

Рассмотрим платёжную матрицу

Предположим, что менеджер действует в условиях полной неопределённости, то есть он не имеет совершенно никакой информации о вероятности различных условий. В этом случае используются следующие критерии:

Максимин	Максимакс	Лаплас	Минимакс регрет
maximin	Maximax	Laplace	Minimax regret
Максимум из минимума (лучший из худших)	Максимум из максимума (лучший из лучших)	Лучший из средних	Наименьший вред
Определяется самая худшая возможная окупаемость для каждой альтернативы и выбирается альтернатива с лучшим из худших значением.	Определяется наилучшая возможная окупаемость и выбирается альтернатива с этим значением	Определяется среднее значение окупаемости для каждой альтернативы и выбирается наилучшая из средних значений альтернатива	Определяются наихудшие возможные последствия для каждой альтернативы и выбирается альтернатива с лучшим из плохих значением.
Пессимистический, по сути, подход, т.к. принимает во внимание только самый худший вариант. Фактический результат может быть не так уж и плох, но этот подход устанавливает гарантированный минимум	Оптимистический, наступательный подход, не принимается во внимание никакой другой вариант кроме лучшего.	Подход определяет обстоятельства как равновероятные

Главный недостаток этих подходов (кроме лаплас), в том, что они не принимают во внимание все возможные результат. Они сосредотачиваются на самомо плохом или самом хорошем и в результате теряется часть информации. При этом слабость метода «Лаплас» состоит в том, что он все условия считает равновероятными.