
3. Определитель матрицы и его свойства.
В этой лекции речь будет идти только о квадратных матрицах.
Каждой квадратной матрице можно поставить в соответствие некоторое число – определитель этой матрицы. Прежде чем дать общее определение, введем определители матриц 2х2 и 3х3.
2.1. Определитель матрицы 2х2.
Назовем определителем матрицы

число,
равное
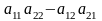 .
.
Обозначения:
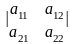 ,
,
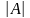 ,
,
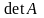 .
.
Пример:
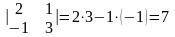 .
.
Определитель матрицы 3х3. Для квадратной матрицы 3-го порядка определитель задается следующим образом:
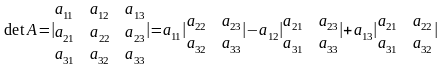 .
.
Раскрывая входящие в это выражение определители второго порядка, получаем:
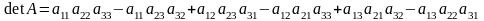 .
.
Несмотря на громоздкость выражения, запомнить его легко.
Тройные произведения элементов матрицы на первой схеме берутся со знаком «+», на второй – со знаком «-.».
Перестановки и подстановки.
Прежде чем обобщить понятие определителя на матрицы более высокого порядка, дадим некоторые новые определения..
Рассмотрим конечное множество из
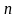 элементов. Занумеруем эти элементы
первыми числами натурального ряда.
Таким образом, будем считать, что
элементами являются числа 1, 2, … .
.
элементов. Занумеруем эти элементы
первыми числами натурального ряда.
Таким образом, будем считать, что
элементами являются числа 1, 2, … .
.
Обычный порядок этих чисел можно изменить, переставив их. Например, числа 1,2,3 можно расположить так: 3,1,2 или 2,3,1. Всякое расположение чисел 1,2,…, назовем перестановкой.
Утверждение. Число всех перестановок множества из элементов равно !.
Доказательство. Общий вид перестановки таков:
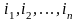 ,
,
где
каждое из
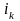 -
одно из чисел
-
одно из чисел
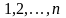 ,
причем все они различны. В качестве
,
причем все они различны. В качестве
 можно взять любое из
чисел. Для каждого выбора числа
есть
можно взять любое из
чисел. Для каждого выбора числа
есть
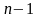 возможность выбрать
возможность выбрать
 .
Если
и
выбраны, то остается
.
Если
и
выбраны, то остается
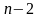 возможности выбрать
возможности выбрать 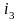 ,
и т.д. Итак, получаем
,
и т.д. Итак, получаем
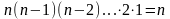 !
!
способов переставить числа 1,2,… . . Ч.т.д.
Подстановкой будем называть
любое взаимно однозначное отображение
множества
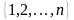 на себя. Чтобы это лучше представить,
запишем одну под другой две строки: в
первой запишем элементы множества
,
а во второй – любую перестановку этих
элементов. Получим
на себя. Чтобы это лучше представить,
запишем одну под другой две строки: в
первой запишем элементы множества
,
а во второй – любую перестановку этих
элементов. Получим
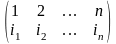
И
будем считать, что при этой подстановке
элемент 1 переходит в
,
элемент 2 – в
и т.д. Очевидно, что каждой подстановке
соответствует перестановка, и это
соответствие взаимно однозначное,
поэтому мы можем записывать подстановку,
указывая только перестановку в нижней
строке. Множество всех подстановок
обозначим
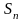 .
Подстановки будем обозначать греческими
буквами
.
Подстановки будем обозначать греческими
буквами
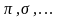 ;
запись
;
запись
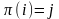 означает, что подстановка
означает, что подстановка
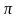 отображает элемент
отображает элемент
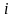 в элемент
в элемент
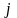 .
.
Четность подстановки.
Пусть
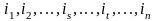 -
-
некоторая
перестановка. Говорят, что
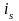 и
и
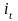 образуют инверсию, если
образуют инверсию, если
 <
<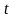 ,
но
>
. Перестановка
называется четной, если она
содержит четное число инверсий, и
нечетной, если число инверсий
нечетно. Например:
,
но
>
. Перестановка
называется четной, если она
содержит четное число инверсий, и
нечетной, если число инверсий
нечетно. Например:
2 3 1 5 4 - 3 инверсии (2,1), (3,1).(5,4); перестановка нечетная.
4 3 1 5 2 - 6 инверсий (4,3), (4,1), (4,2), (3,1), (3,2), (5,2); перестановка четная.
Установленное выше соответствие между
перестановками и подстановками позволяет
говорить и о четности подстановок: будем
называть подстановку четной (нечетной),
если соответствующая ей перестановка
четная (нечетная). Знак подстановки
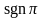 равен +1, если подстановка четная, и -1,
если подстановка нечетная.
равен +1, если подстановка четная, и -1,
если подстановка нечетная.
Лемма. Две перестановки
 и
и
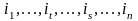
имеют различную четность.
Доказательство. Пусть сначала
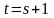 ,
т.е. вторая получается из первой
перестановкой двух соседних элементов:
,
т.е. вторая получается из первой
перестановкой двух соседних элементов:
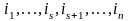 ;
;
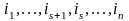 .
.
Инверсии,
содержащиеся в первой перестановке,
в которых хотя бы один элемент не равен
или
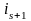 сохраняются и во второй перестановке.
Исключение составляет пара
сохраняются и во второй перестановке.
Исключение составляет пара
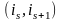 .
Если она образует инверсию, то во
второй перестановке пара
.
Если она образует инверсию, то во
второй перестановке пара
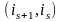 инверсии
не образует. И наоборот, если инверсии
не было, то во второй перестановке,
поменявшись местами, эти элементы
образуют инверсию. Значит, количество
инверсий в этих перестановках отличается
на одну инверсию.
инверсии
не образует. И наоборот, если инверсии
не было, то во второй перестановке,
поменявшись местами, эти элементы
образуют инверсию. Значит, количество
инверсий в этих перестановках отличается
на одну инверсию.
Пусть теперь и произвольные. Тогда вторую перестановку можно получить из первой за несколько шагов, каждый раз меняя соседние элементы:
и
,
и
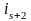 ,…,
и
- всего
,…,
и
- всего  шагов;
шагов;
затем
и
 ,
и
,
и
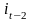 ,…,
и
- всего
,…,
и
- всего
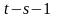 шагов.
шагов.
Итого,
мы сделаем
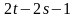 шагов. На каждом шаге знак перестановки
менялся, а поскольку число шагов было
нечетно, то знаки перестановок различны.
шагов. На каждом шаге знак перестановки
менялся, а поскольку число шагов было
нечетно, то знаки перестановок различны.
