3. Признак Лейбница сходимости знакочередующегося ряда.

Признак Лейбница – признак сходимости знакочередующегося ряда. Формулировка:

Пусть для знакочередующегося ряда выполняются следующие условия:

(монотонное невозрастание )

то ряд сходится.

Если выполнены все условия, и ряд из модулей () сходится, то исходный ряд сходится абсолютно. Если выполнены все условия, но ряд из модулей расходится, то исходный ряд сходится условно.

Строгая положительность a_n существенна.

Ряды, удовлетворяющие признаку Лейбница, называются рядами Лейбница. Следует отметить, что этот признак является достаточным, но не необходимым.

Билет №2

1. Теорема о среднем для определённого интеграла.

Если f(x) непрерывна на отрезке [a,b], то существует точка , такая что .

Док-во. Функция, непрерывная на отрезке, принимает на этом отрезке своё наименьшее m и наибольшее M значения. Тогда . Число заключено между минимальным и максимальным значениями функции на отрезке. Одно из свойств функции, непрерывной на отрезке, заключается в том, что эта функция принимает любое значение, расположенное между m и M. Таким образом, существует точка , такая что .

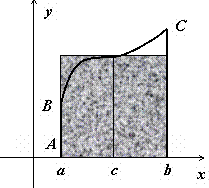
Это свойство имеет простую геометрическую интерпретацию: если непрерывна на отрезке [a,b], то существует точка такая, что площадь криволинейной трапеции ABCD равна площади прямоугольника с основанием [a,b] и высотой f(c) (на рисунке выделен цветом).

2. Формула замены переменной в определённом интеграле.

Пусть функция :

1. определена, непрерывно дифференцируема и монотонна на отрезке ,

2. ,

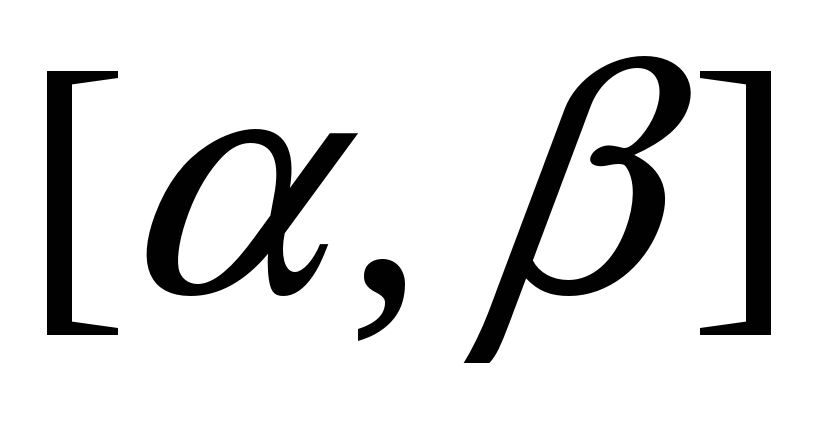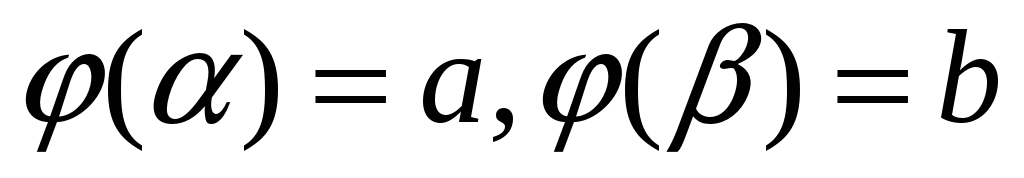3. функция 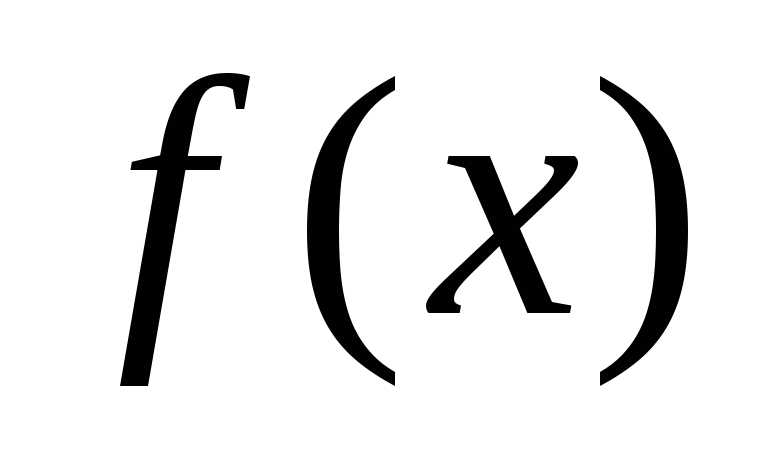непрерывна на отрезке [a, b].

Тогда .

Док-во. Пусть F(x) - первообразная для функции f(x), т.е. , тогда - первообразная для функции .

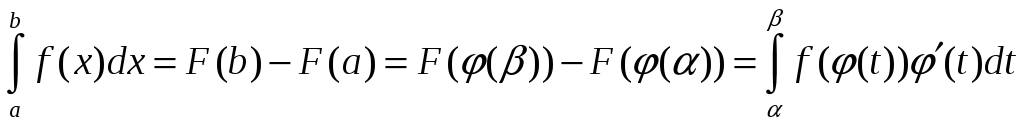, что и требовалось доказать.

При решении задач нельзя забывать о том, что при переходе к новой переменной надо обязательно вычислить новые пределы интеграла.

Пример:

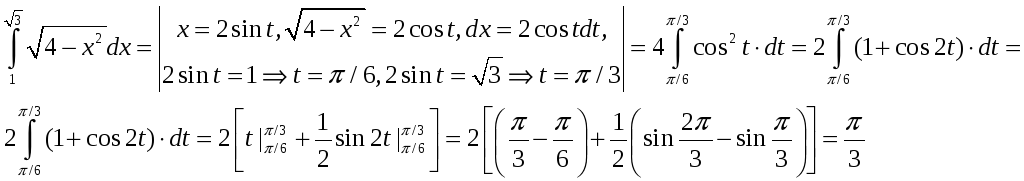
3. Интегральный признак сходимости числового ряда

Интегральный признак Коши — признак сходимости убывающего положительного числового ряда. Признак Коши даёт возможность свести проверку сходимости ряда к проверке сходимости несобственного интеграла соответствующей функции на , последний часто может быть найден в явном виде.

Пусть для функции f(x) выполняется:

1. (функция принимает только положительные значения)

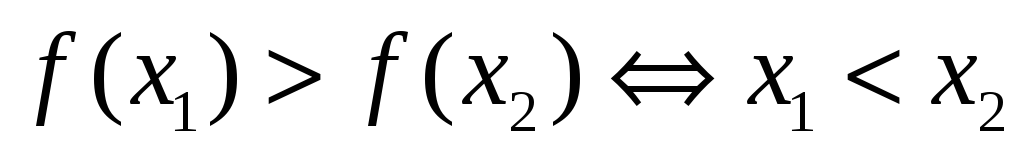2. (функция монотонно убывает)

3. 

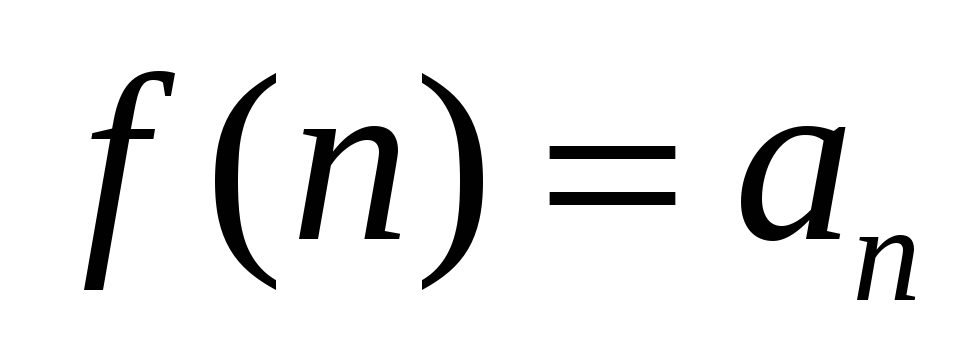
Тогда ряд и несобственный интеграл сходятся или расходятся одновременно, смотря по тому, сходится или расходится интеграл.

Набросок доказательства:

1. Построим на графике f(x) ступенчатые фигуры.

2. Площадь большей фигуры равна

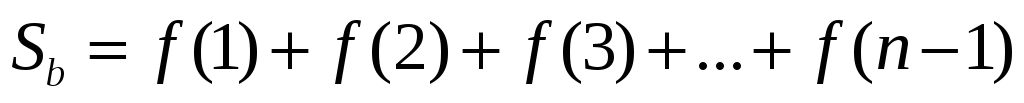
3. Площадь меньшей фигуры равна

4. Площадь криволинейной трапеции под графиком функции равна

5. Получаем

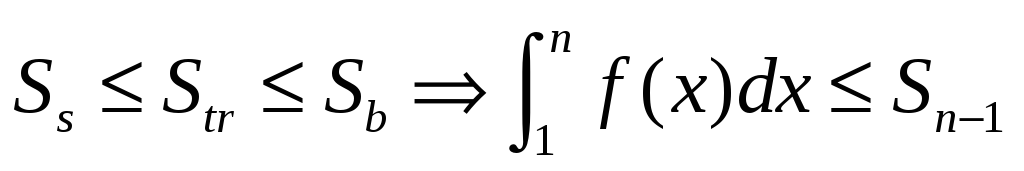
6. Далее доказывается с помощью критерия сходимости знакоположительных рядов.

Примеры:

расходится, так как

сходится, так как

Билет №3

1. Критериий Коши сходимости числового ряда.

Для того, чтобы ряд был сходящимся необходимо и достаточно, чтобы для любого существовал номер N такой, что при n>N и любом p>0 выполнялось бы неравенство

.

Однако, на практике использовать непосредственно критерий Коши не очень удобно. Поэтому, как правило, используются более простые признаки сходимости:

1) Если ряд сходится, то необходимо, чтобы общий член u_n стремился к нулю. Однако это условие не является достаточным. Можно говорить только о том, что если общий член не стремится к нулю, то ряд точно расходится. Например, так называемый гармонический ряд является расходящимся, хотя его общий член и стремится к нулю.

Пример. Исследовать сходимость ряда

Найдем 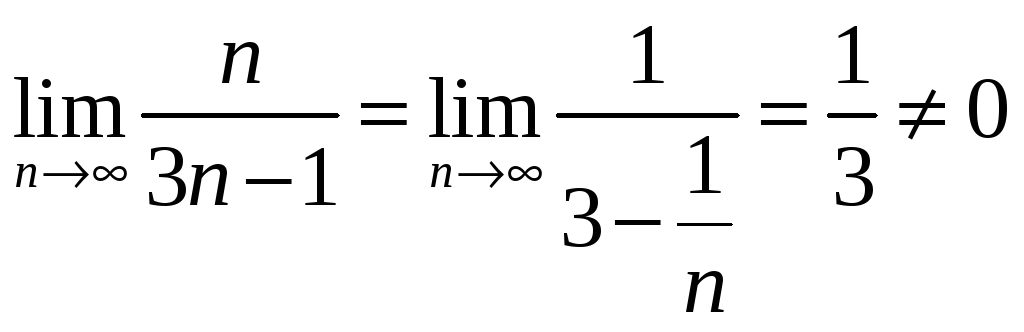- необходимый признак сходимости не выполняется, значит ряд расходится.