
- •1. Формула Ньютона-Лейбница.
- •1. Теорема о среднем для определённого интеграла.
- •1. Определение интеграла Римана.
- •1. Теорема о среднем для определённого интеграла.
- •Билет №1
- •1. Формула интегрирования по частям для определённого интеграла.
- •2. Признак сравнения для ряда с неотрицательными членами.
- •3. Признак Лейбница сходимости знакочередующегося ряда.
- •Билет №2
- •1. Теорема о среднем для определённого интеграла.
- •2. Формула замены переменной в определённом интеграле.
- •3. Интегральный признак сходимости числового ряда
- •Билет №3
- •1. Критериий Коши сходимости числового ряда.
- •2. Признак Даламбера.
- •3. Формула Ньютона-Лейбница.
- •Билет №4
- •1. Определение первообразной и неопределённого интеграла.
- •2. Подстановки Эйлера.
- •3. Формула интегрирования по частям для неопределённого интеграла.
- •Билет №5
- •1. Определение первообразной и неопределенного интеграла.
- •2. Интегрирование рациональной функции.
- •3. Обьём тела вращения.
- •Билет №6
- •1. Формула Ньютона-Лейбница.
- •2. Схема исследования функции.
- •3. Первообразная и неопределенный интеграл.
- •Билет №7
- •1. Теорема о среднем для определённого интеграла.
- •2. Понятие суммы ряда. Необходимое условие сходимости.
- •3. Определение интеграла Римана.
- •Билет №8
- •1. Понятие длины кривой. Достаточное условие спрямляемости кривой.
- •2. Формула интегрирования по частям для определенного интеграла.
- •3 Определение обьёма тела.
- •Билет №9
- •1. Определение интеграла Римана.
- •3. Площадь криволинейной трапеции и криволинейного сектора.
- •Билет №10
- •1. Определение первообразной и неопределённого интеграла. Вычисление интегралов
- •2. Формула замены переменной в неопределённом интеграле.
- •3. Интегралы от рациональной функции от sin X и cos X. Методы вычисления.
- •Билет №11
- •1. Теорема о среднем для определённого интеграла.
- •2. Формула замены переменной в определенном интеграле.
- •3. Подстановки Эйлера.
Билет №9
1. Определение интеграла Римана.
Риман формализовал понятие интеграла, разработанное Ньютоном и Лейбницем, как площади подграфика (фигуры, заключенной между графиком функции и осью абсцисс). Для этого он рассмотрел фигуры, состоящие из нескольких вертикальных прямоугольников и получающиеся при разбиении отрезка (см. рисунок). Если при «размельчении» разбиения существует предел, к которому сходятся площади таких фигур (интегральные суммы), этот предел называется интегралом Римана функции на отрезке.
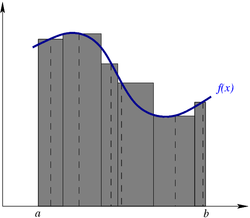
Определение через интегральные суммы:
Пусть на отрезке [a,b] определена вещественнозначная функция f.
Рассмотрим разбиение отрезка
![]() — конечное множество попарно различных
точек отрезка. Это разбиение делит
отрезок [a,b] на n отрезков . Длина
наибольшего из отрезков δR =max(Δxi),
называется шагом разбиения, где Δxi
= xi − xi − 1
– длина элементарного отрезка.
— конечное множество попарно различных
точек отрезка. Это разбиение делит
отрезок [a,b] на n отрезков . Длина
наибольшего из отрезков δR =max(Δxi),
называется шагом разбиения, где Δxi
= xi − xi − 1
– длина элементарного отрезка.
Отметим на каждом отрезке разбиения по
точке
![]() .
Интегральной суммой называется выражение
.
Интегральной суммой называется выражение
![]() .
.
Если при стремлении шага разбиения к
нулю интегральные суммы стремятся к
одному и тому же числу, независимо от
выбора
![]() ,
то это число называется интегралом
функции f на отрезке [a,b], т.е.
,
то это число называется интегралом
функции f на отрезке [a,b], т.е.
![]() .
.
В этом случае, сама функция f называется интегрируемой (по Риману) на [a,b]; в противном случае f является неинтегрируемой (по Риману) на отрезке [a,b].
Свойства:
-
Невырожденность:

-
Положительность: Если интегрируемая функция f неотрицательна, то её интеграл по отрезку [a,b] также неотрицателен.
-
Линейность: Если функции f и g интегрируемы, и
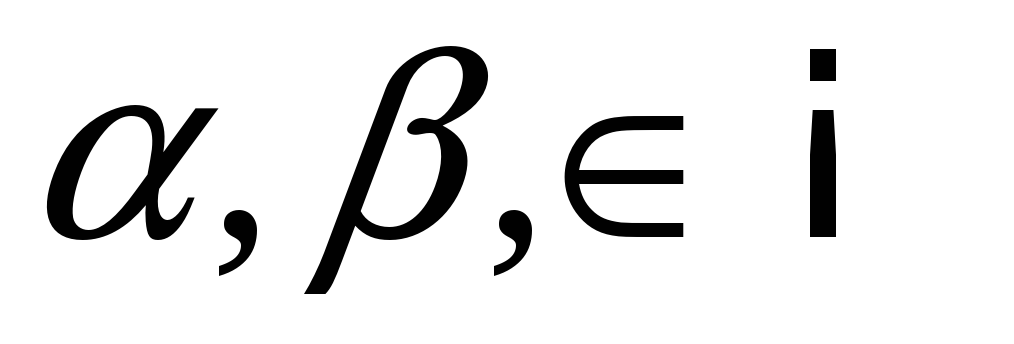 ,
то функция αf + βg
тоже интегрируема, и
,
то функция αf + βg
тоже интегрируема, и
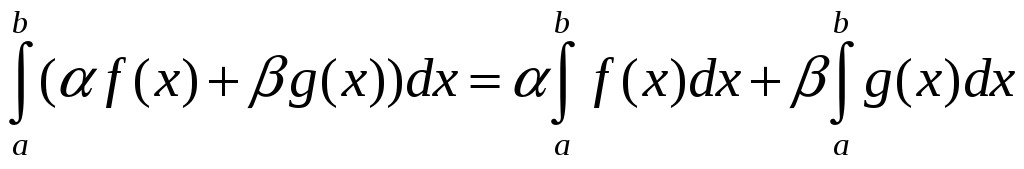 .
. -
Непрерывность: Если интегрируемые функции fi равномерно сходятся на отрезке [a,b] к функции f, то f интегрируема, и
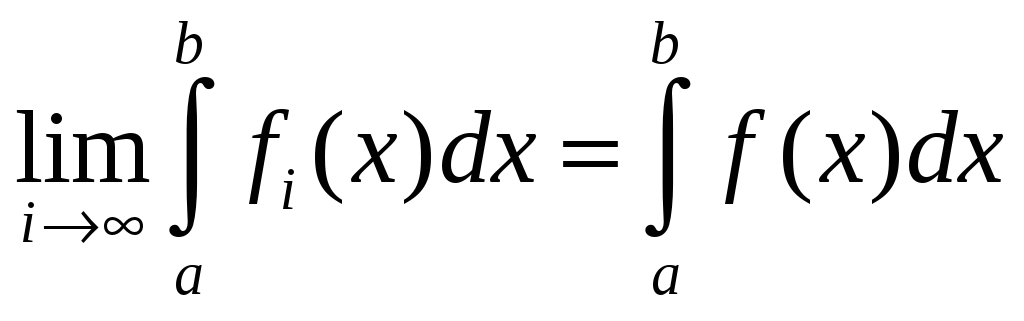 .
(Последняя формула может быть получена
уже как формальное следствие свойств
1-3 и интегрируемости предельной функции.)
.
(Последняя формула может быть получена
уже как формальное следствие свойств
1-3 и интегрируемости предельной функции.) -
Аддитивность при разбиениях отрезка Пусть a < b < c. Функция f интегрируема на отрезке [a,c], тогда и только тогда, когда она интегрируема на каждом из отрезков [a,b] и [b,c], при этом
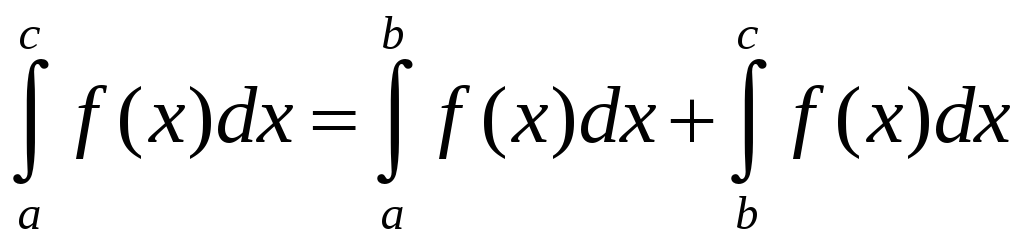 .
. -
Непрерывная на отрезке функция интегрируема по Риману (следствие свойств 1-5). Разрывные функции могут быть интегрируемы, но могут и не быть; примером функции, не интегрируемой по Риману, является всюду разрывная функция Дирихле. Критерий Лебега интегрируемости функции по Риману: функция интегрируема по Риману на отрезке [a,b], если и только если на этом отрезке она ограничена, и множество точек, где она разрывна, имеет нулевую меру (то есть может быть покрыто счётным семейством интервалов со сколь угодно малой суммарной длиной).
-
Если функция F является первообразной непрерывной функции f, то интеграл функции f на отрезке [a,b] может быть вычислен по формуле Ньютона-Лейбница: он равен F(b) − F(a). (Это - общее свойство любых интегралов, удовлетворяющих свойствам 1-5, а не только интеграла Римана.) Непрерывная на отрезке функция f всегда имеет первообразную, и каждая первообразная имеет вид:
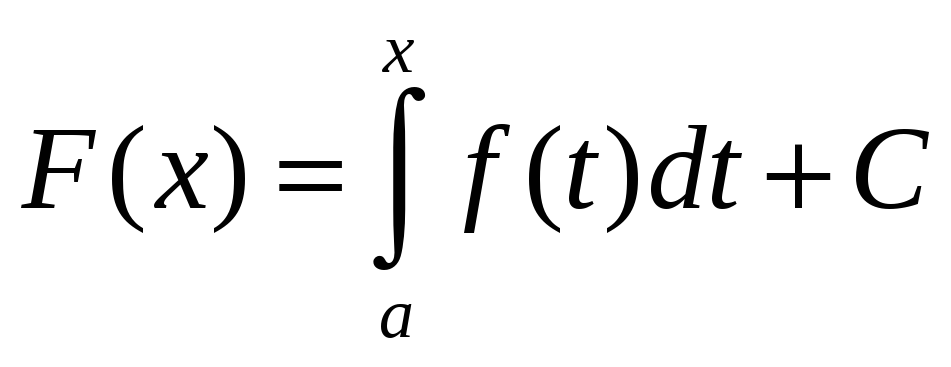 ,
где C - произвольная
константа.
,
где C - произвольная
константа.
2. Суммы Дарбу. Критерий интегрируемости функции, ограниченной на отрезке.
Пусть на отрезке [a,b] определена
вещественнозначная функция f.
Рассмотрим разбиение
![]() .
.
Введем обозначения
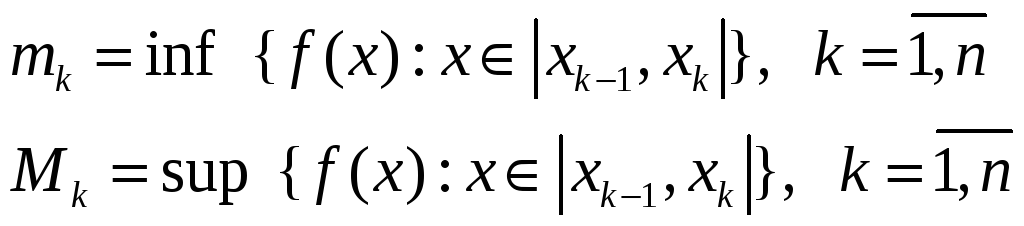 ,
,
Наконец, рассмотрим суммы
![]() – нижняя сумма Дарбу,
– нижняя сумма Дарбу,
![]() – верхняя сумма Дарбу.
– верхняя сумма Дарбу.
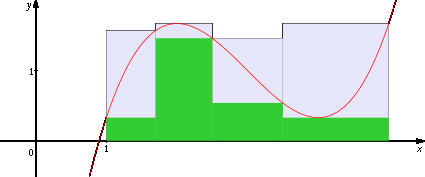 Нижняя (зеленая) и верхняя (серая) суммы
Дарбу
Нижняя (зеленая) и верхняя (серая) суммы
Дарбу
Критерий Дарбу интегрируемости функции
Приведенные утверждения даны для функции одной переменной.
Пусть вещественнозначная функция
![]() определена и ограничена на отрезке
определена и ограничена на отрезке
![]() .
Пусть
.
Пусть
![]() и
и
![]() - верхний и нижний интегралы Дарбу
функции
- верхний и нижний интегралы Дарбу
функции
![]() на заданном отрезке соответственно.
Тогда следующие 3 условия эквивалентны:
на заданном отрезке соответственно.
Тогда следующие 3 условия эквивалентны:
![]() интегрируема по Риману на отрезке
интегрируема по Риману на отрезке
![]() ,
,
![]() ,
,
![]() ,
где τ и Δτ — некоторое разбиение и его
мелкость.
,
где τ и Δτ — некоторое разбиение и его
мелкость.
