2. Формула замены переменной в неопределённом интеграле.

Пусть функция :

4. определена, непрерывно дифференцируема и монотонна на отрезке ,

5. ,

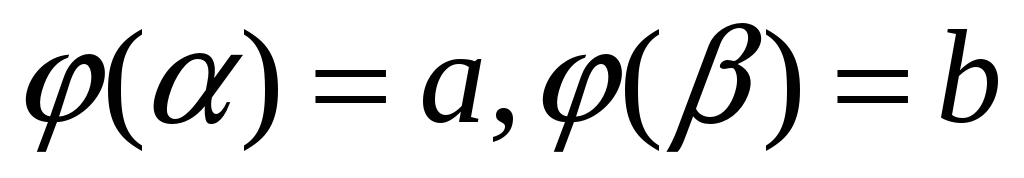6. функция 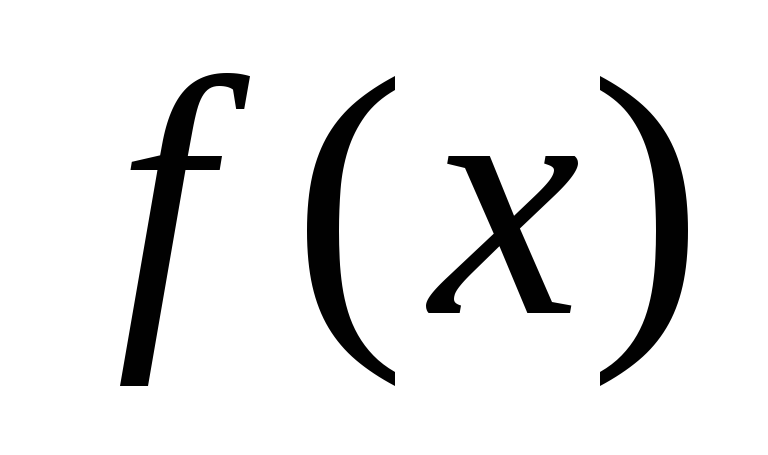непрерывна на отрезке [a, b].

Тогда .

Док-во. Пусть F(x) - первообразная для функции f(x), т.е. , тогда - первообразная для функции .

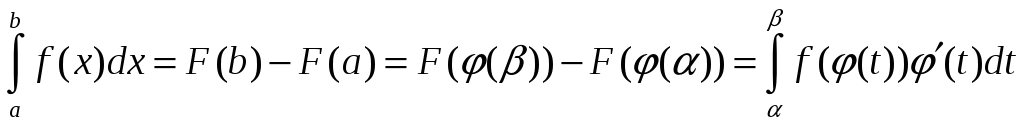, что и требовалось доказать.

При решении задач нельзя забывать о том, что при переходе к новой переменной надо обязательно вычислить новые пределы интеграла.

Пример:

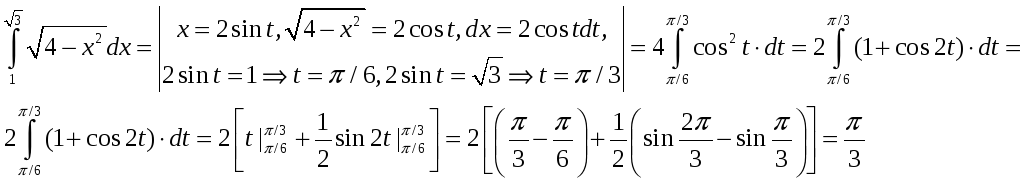
3. Интегралы от рациональной функции от sin X и cos X. Методы вычисления.

Интегралов от тригонометрических функций может быть бесконечно много. Большинство из этих интегралов вообще нельзя вычислить аналитически, поэтому рассмотрим некоторые главнейшие типы функций, которые могут быть проинтегрированы всегда.

Интеграл вида .

Здесь R – обозначение некоторой рациональной функции от переменных sinx и cosx.

Интегралы этого вида вычисляются с помощью подстановки . Эта подстановка позволяет преобразовать тригонометрическую функцию в рациональную.

,

Тогда

Таким образом:

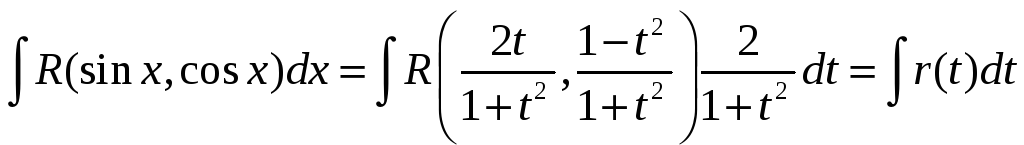
Описанное выше преобразование называется универсальной тригонометрической подстановкой.

Пример: 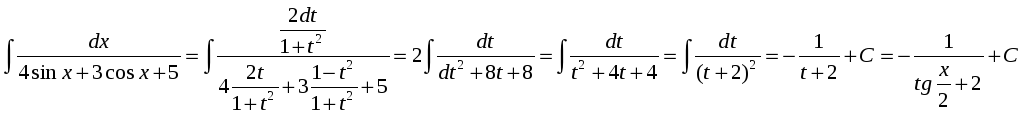Несомненным достоинством этой подстановки является то, что с ее помощью всегда можно преобразовать тригонометрическую функцию в рациональную и вычислить соответствующий интеграл. К недостаткам можно отнести то, что при преобразовании может получиться достаточно сложная рациональная функция, интегрирование которой займет много времени и сил.

Однако при невозможности применить более рациональную замену переменной этот метод является единственно результативным.

Билет №11

1. Теорема о среднем для определённого интеграла.

Если f(x) непрерывна на отрезке [a,b], то существует точка , такая что .

Док-во. Функция, непрерывная на отрезке, принимает на этом отрезке своё наименьшее m и наибольшее M значения. Тогда . Число заключено между минимальным и максимальным значениями функции на отрезке. Одно из свойств функции, непрерывной на отрезке, заключается в том, что эта функция принимает любое значение, расположенное между m и M. Таким образом, существует точка , такая что .

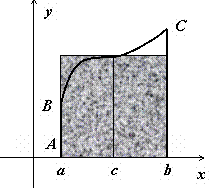
Это свойство имеет простую геометрическую интерпретацию: если непрерывна на отрезке [a,b], то существует точка такая, что площадь криволинейной трапеции ABCD равна площади прямоугольника с основанием [a,b] и высотой f(c) (на рисунке выделен цветом).

2. Формула замены переменной в определенном интеграле.

Пусть функция :

1. определена, непрерывно дифференцируема и монотонна на отрезке ,

2. ,

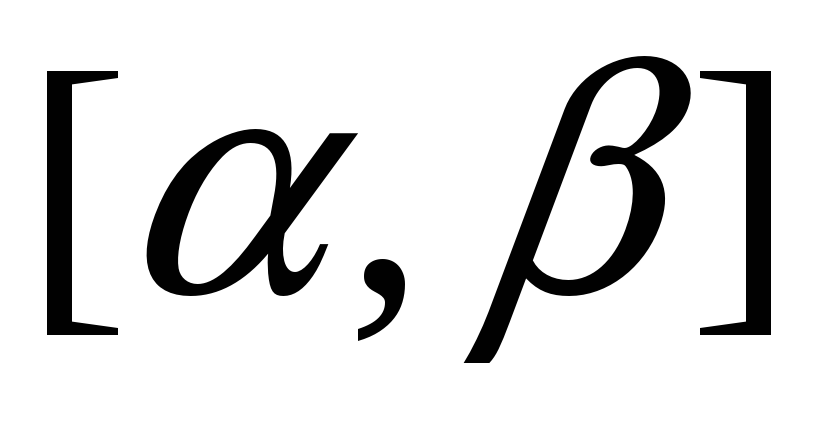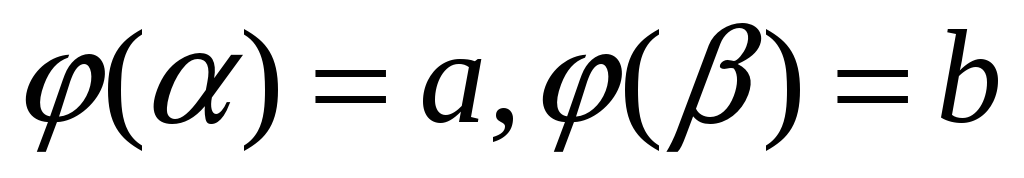3. функция непрерывна на отрезке [a, b].

Тогда .

Док-во. Пусть F(x) - первообразная для функции f(x), т.е. , тогда - первообразная для функции .

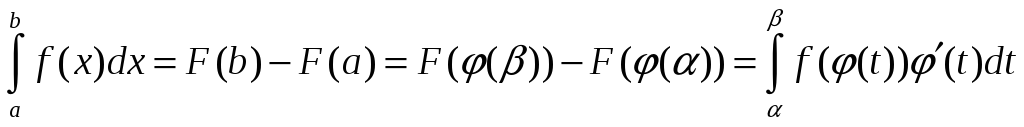, что и требовалось доказать.

При решении задач нельзя забывать о том, что при переходе к новой переменной надо обязательно вычислить новые пределы интеграла.

Пример:

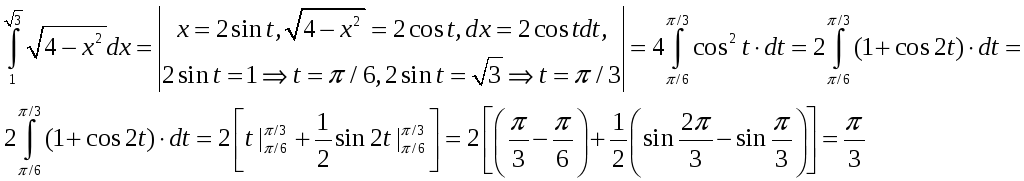
3. Подстановки Эйлера.

Подстановки, служащие для приведения интегралов вида , где

R (x, y) — рациональная функция от х и у, к интегралам от рациональных функций. Предложены Эйлером в 1768.

Первая Эйлерова подстановка применима, если а>0;

Вторая Эйлерова подстановка применима, если с > 0;

Третья Эйлерова подстановка где λ — один из корней трёхчлена , применима, если корни этого трёхчлена действительны. На практике Э. п. требуют громоздких преобразований и потому вместо них обычно пользуются теми или иными искусственными приёмами, упрощающими вычисление.

Аналогичные подстановки делаются в теории чисел при решении неопределённых уравнений 2-й степени в рациональных числах.