1.4 Выборочное наблюдение

Выборочное наблюдение будем проводить на основе данных, представленных в таблице 1.14.5.

Таблица 1.4.15

№	Количество отработанных чел.-смен
1	70,38
2	72,42
3	71,40
4	76,50
5	82,62
6	104,04
7	78,54
8	80,58
9	77,52
10	81,60
11	83,64
12	106,08
13	98,94
14	94,86
15	99,96
16	86,70
17	74,46
18	79,56
19	85,68
20	88,74
21	94,86
22	97,92
23	96,90
24	99,96
25	113,22
26	116,28
27	100,98
28	90,78
29	78,54
30	82,62
31	83,64
32	109,14
33	108,12
34	107,10
35	106,08
36	105,06
37	104,04
38	102,00
39	103,02
40	117,30
41	119,34
42	121,38

1.4.1 Случайная бесповторная выборка

Проведем случайную бесповторную выборку с объемом выборки равном 32 единицам. Для этого создадим выборочную совокупность из 32 произвольно выбранных единиц, а затем представим ее в виде следующей таблицы 1.4.16.

Таблица 1.4.16

№	Количество отработанных чел.-смен
1	70,38
2	72,42
3	71,4
4	76,5
5	82,62
6	104,04
7	78,54
8	80,58
9	77,52
10	81,6
11	83,64
12	106,08
13	98,94
14	94,86
15	99,96
16	86,7
17	74,46
18	79,56
19	85,68
20	88,74
21	97,92
22	96,9
23	113,22
24	116,28
25	100,98
26	90,78
27	78,54
28	109,14
29	108,12
30	107,1
31	105,06
32	104,04
Итого	2922,3

Определим среднюю величину при случайной бесповторной выборке, которая находится по формуле:

(1.4.45),

где - дисперсия;

- объем выборочной совокупности;

- объем генеральной совокупности.

Прежде чем определить среднюю величину найдем дисперсию, находится по формуле простой дисперсии ,так как нам не известны удельные веса показателей, которые изучаются:

(1.4.46).

Для дисперсии найдем по формуле 1.4.3. Будем искать простую среднюю, так как не известны удельные веса изучаемых показателей.

(1.4.47).

Таким образом,

991,32

Для расчета дисперсии составим вспомогательную таблицу 1.4.17.

Таблица 1.4.17

№	Количество отработанных чел.-смен
1	70,38	438,56
2	72,42	357,28
3	71,4	396,88
4	76,5	219,69
5	82,62	75,72
6	104,04	161,75
7	78,54	163,38
8	80,58	115,39
9	77,52	190,49
10	81,6	94,51
11	83,64	59,01
12	106,08	217,80
13	98,94	58,04
14	94,86	12,52

Продолжение таблицы 1.4.17

15	99,96	74,62
16	86,7	21,36
17	74,46	284,32
18	79,56	138,34
19	85,68	31,83
20	88,74	6,67
21	97,92	43,54
22	96,9	31,12
23	113,22	479,53
24	116,28	622,91
25	100,98	93,28
26	90,78	0,29
27	78,54	163,38
28	109,14	317,49
29	108,12	282,18
30	107,1	248,95
31	105,06	188,74
32	104,04	161,75
Итого	2922,3	5751,30

Таким образом

Теперь можно определить среднюю величину, которая равна

(чел.-смен)

Найдем предельную ошибку репрезентативности случайной бесповторной выборки при определении средней величины по следующей формуле:

(1.4.48),

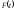где - коэффициент доверия, который зависит от вероятности , с которой гарантируется значение предельной ошибки выборки.

Так как , то .

Таким образом, предельная ошибка репрезентативности случайной бесповторной выборки при определении средней величины :

(чел.-смен)

Далее рассчитаем относительную ошибку выборки, которая вычисляется по формуле:

(1.4.49)

Теперь можно найти границы, в которых находится генеральная средняя по формуле:

(1.4.50),

Таким образом, с вероятностью 0,954 можно утверждать, что генеральное среднее количество отработанных чел.-смен находится в пределах от 89 до 94.

Признаком для определения долей будет количество отработанных чел.-смен ,меньше 80.

Далее определим долю в выборочной совокупности (выборочную долю) по формуле:

(1.4.51),

где - выборочная доля, которую можно найти по следующей формуле:

(1.4.52),

где - число единиц выборочной совокупности, которые владеют признаком, который изучается.

В данном случае признаку соответствуют 9 показателей.

Таким образом, .

Теперь можно определить выборочную долю

Найдем предельную ошибку репрезентативности случайной бесповторной выборки при определении доли по следующей формуле:

(1.4.53),

где - коэффициент доверия, который зависит от вероятности , с которой гарантируется значение предельной ошибки выборки.

Так как , то .

Таким образом, предельная ошибка репрезентативности случайной бесповторной выборки при определении доли равна 0,074 или 7.4%.

Далее рассчитаем относительную ошибку выборки, которая вычисляется по формуле:

(1.4.54)

Теперь можно найти границы, в которых находится доля по формуле:

(1.4.55),

.

Таким образом, с вероятностью 0,954 можно утверждать, что генеральная доля работников с количеством отработанных чел.-смен меньше 70 находится в пределах от 17,5% до 32,5%.