6.4. Параметрический резонанс.

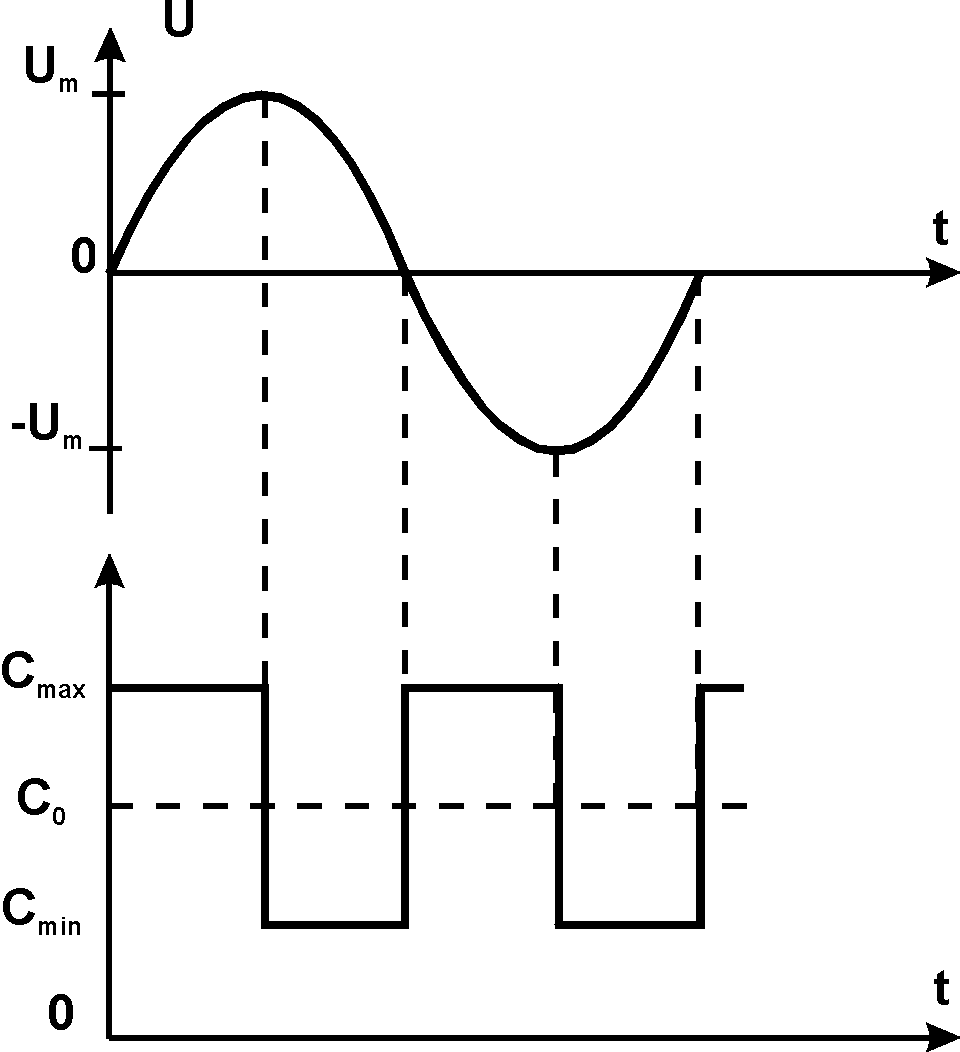
Существуют явления, при которых, также как и при действии гармонического сигнала на колебательный контур, результат внешнего воздействия называется зависимым от частоты этого воздействия. Эти явления объединяют понятием “резонанс” в более широком смысле, и применительно к колебательным цепям, содержащих параметрический конденсатор, говорят о параметрическом резонансе.

Рассмотрим в качестве примера явления, происходящие в колебательном контуре с параметрическим конденсатором при воздействии на конденсатор напряжения накачки в виде прямоугольных импульсов с частотой следования, равной удвоенной частоте собственных колебаний контура. Допустим, что между частотой собственных колебаний и изменением емкости С существует жесткая синхронизация: в моменты времени, когда напряжение на конденсаторе достигает экстремума, емкость скачком уменьшается: в моменты времени, когда напряжение становится равным нулю, емкость скачком увеличивается на ту же величину (см. рис.).

Энергия, запасенная конденсатором, равна . При малом приращении емкости С<<C₀ приращение энергии

(19)

(линейно зависит от приращения емкости)

Максимальная энергия, запасенная параметрическим конденсатором, равна

Из графиков и формулы (19) следует, что за период собственных колебаний контур дважды получает дополнительную энергию от источника накачки в моменты экстремальных значений напряжения на конденсаторе. Обозначим эту дополнительную энергию накачки Е_НК, и, в соответствии с формулой (19), запишем

(20)

Как известно, эквивалентное сопротивление контура при резонансе активно и для параллельного контура равно R_ЭКВ=Q, где Q - добротность, а - характеристическое сопротивление контура. Энергия, рассматриваемая в контуре за период собственных колебаний, равна

(21)

Сравнивая рассеиваемую энергию (21) с накачиваемой в контур (20), можно заключить, что в контуре колебания либо не возникают, либо они нарастают неограниченно. первое происходит, если Е_РАСС>E_НК; второе - если Е_РАСС<E_НК. Другими словами, колебания нарастают, если коэффициент модуляции емкости больше некоторого критического значения. Из (20) и (21) также следует, что для возникновения параметрического резонанса необходимо, чтобы выполнить условие

Подставив сюда , получим

Оно и определяет критическое значение ΔС.

Поясним полученный результат. Каждый раз, когда емкость уменьшается, конденсатор заряжен и энергия источника накачки затрачивается на увеличение электрической энергии контура. Каждый раз, когда емкость увеличивается, конденсатор разряжен и изменение емкости происходит без затрат полезной энергии.

Таким образом в цепях с реактивными параметрическими элементами энергия накачки может преобразовываться в энергию сигнала.

6.5. Баланс мощностей в параметрических цепях.

Рассматриваемая модель параметрической цепи реально представляет собой нелинейную цепь. А в цепи, содержащей нелинейный конденсатор, под воздействием напряжения генератора накачки и напряжения генератора сигнала, возникают колебания комбинационных частот

Чтобы представить себе как перераспределяется энергия информационного сигнала и сигнала накачки между комбинационным колебанием рассмотрим следующую цепь.

Пусть параллельно нелинейному конденсатору включены три цепи: цепь накачки, цепь сигнала и колебательный контур. Последний называют холостым контуром. Контур настроен на одну из комбинационных частот _к, и, поэтому, можно принять, что других комбинационных колебаний не существует. Сумма средних мощностей колебаний сигнала P_C, накачки P_НК и комбинационной частоты P_К должна быть равна нулю(закон сохранения энергии):

(21)

Переходя в (21) от средних мощностей к энергиям в соответствии с (17) получим: Подставляя сюда находим, что

(22)

Равенство (22) при произвольных и выполняется, если каждое слагаемое равно нулю (поскольку они не связаны общей частотой):

Переходя от энергии к средним мощностям получаем:

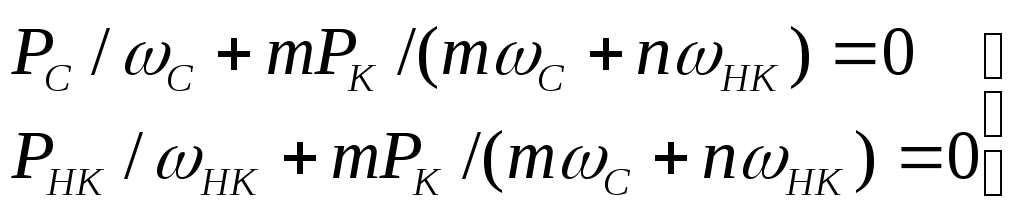(23)

Уравнения (23) выражают закон сохранения энергии в параметрических цепях. Их называют уравнениями Мэнли-Роу. И они являются частным случаем общей теоремы Мэнли-Роу о балансе мощностей в спектре колебания параметрической цепи, содержащей реактивную нелинейность (емкость или индуктивность). Теорема записывается в виде:

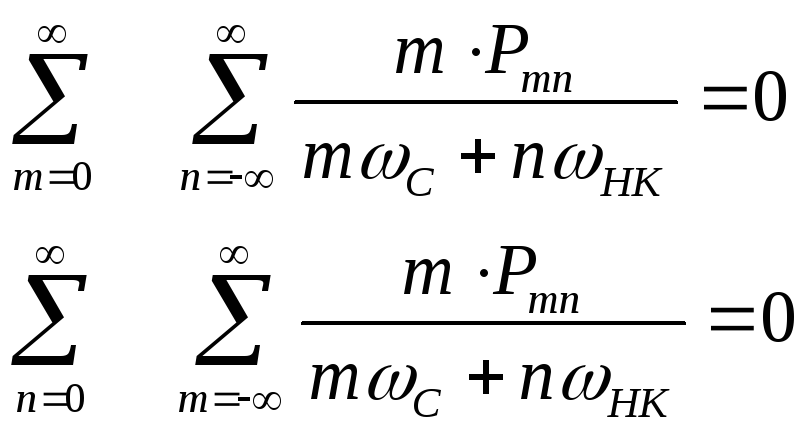
Они определяют законы распределения энергии сигнала накачки между гармониками выходного сигнала

Здесь P_mn - средняя мощность колебания на комбинационной частоте .

Запишем уравнения Мэнли-Роу для частного вида цепи, в которой существуют колебания только на четырех частотах:

.

Для этого в (23) необходимо задать две пары значений m и n: m=1, n=1 и m=-1, n=1.

Тогда

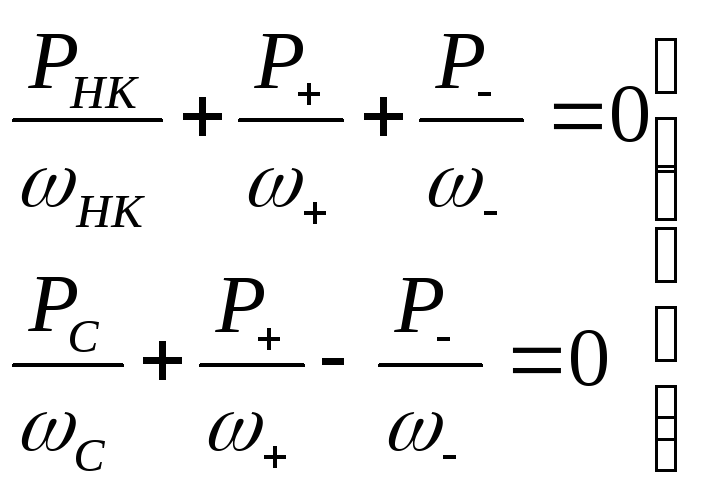(24)

Эти формулы и устанавливают количественные соотношения (баланс) между мощностями колебаний различных частот.