§ 5. Класифікація магнетиків

5.1. Магнітний момент атома, класифікація магнетиків

Природа молекулярних струмів стала зрозуміла після того, як Резерфорд дослідно встановив, що атоми всіх речовин складаються з позитивно зарядженого ядра і негативно заряджених електронів. Рух електронів підпорядковується квантовім законам і таке поняття як траєкторія для електронів не застосовується. Але для пояснення деяких явищ, таких як намагнічування магнетиків, можна використати одну з моделей атома, наприклад Борівську, згідно якої електрони в атомах рухаються по стаціонарним круговим орбітам.

За значенням величини магнітної проникності всі магнетики поділяють на:

• діамагнетики (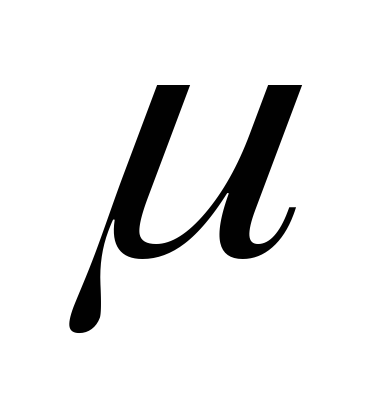<1);

• парамагнетики (>1);

• феромагнетики (>>1).

5.2. Діамагнетики

У більшості атомів діамагнетиків немає власних магнітних моментів і його магнітний момент індукується зовнішнім полем, подібно до того, як виникає електричний момент у неполярних діелектриках.

Якщо врахувати, що наведений магнітний момент пропорційний зовнішньому полю індукцією В₀, можна записати

.

В даному випадку магнітна проникність <1.

Розглянемо на прикладі Борівської моделі природу діамагнетизму. Нехай електрон рухається з деякою швидкістюV по орбіті радіуса R.

Через площину, яка розташована в будь-якому місці на шляху електрона за одиницю часу переноситься заряд , дее – заряд електрона, – число обертів за одиницю часу.

Рис. 5.1

Електрон утворює коловий струм I, направлений протилежно напрямку руху електрона (оскільки заряд електрона негативний) і даний струм чисельно дорівнює:

I=.

Магнітний момент струму, який створює електрон – p_m:

Величина дасть нам швидкість V. Тоді

. (5.1)

Момент, обумовлений рухом електрона по орбіті називається орбітальним магнітним моментом електрона.

Напрямок вектора p_m утворює з напрямом вектора намагнічування J правогвинтову систему (правило свердлика).

Електрон, що рухається по коловій орбіті має момент імпульсу М:

. (5.2)

Вектор М називається орбітальним механічним моментом електрона і утворює з напрямом руху електрона правогвинтову систему. Відношення магнітного моменту елементарної частинки до її механічного моменту називається магнітомеханічним, або гіромагнітним відношенням.

Для електрона гіромагнітне відношення

. (5.3)

Знак „мінус” вказує на те, що напрямок руху магнітного p_m і орбітального М моментів різний. В результаті руху навколо ядра електрон стає подібним до дзиґи і дане явище лежить в основі магнітомеханічних явищ. Намагнічування магнетиків приводить до його обертання і навпаки – обертання магнетика викликає його намагнічування.

Діамагнітний ефект не залежить від температури, оскільки тепловий рух атомів не порушує орієнтації індукованих струмів всередині атомів. Діамагнітний ефект властивий будь-якій речовині.

До діамагнетиків відносяться: вода, деякі метали (золото, ртуть, мідь), інертні гази.

5.3. Парамагнетики

Молекули парамагнетиків мають відмінні від нуля власні магнітні моменти і, якщо зовнішнього магнітного поля немає, ці моменти розміщуються хаотично, тому сумарний вектор намагнічування дорівнює нулю.

Якщо парамагнетик внести в магнітне поле, то магнітні моменти окремих атомів або молекул орієнтуються за напрямом поля так, що власне поле парамагнетика підсилює зовнішнє поле. Якщо такий ефект існує, то він завжди має перевагу над діамагнетизмом.

Властивості парамагнетиків:

• Тепловий рух атомів і молекул руйнує взаємну орієнтацію магнітних моментів молекул і тому намагніченість парамагнетиків залежить від температури і відносна магнітна проникність парамагнетиків спадає із збільшенням температури.

• Відносна магнітна проникність парамагнетиків, як і діамагнетиків, не залежить від магнітної індукції зовнішнього магнітного поля.

До парамагнетиків слід віднести: лужні метали, кисень, алюміній, платину.

5.4. Феромагнетики

Феромагнетизм – граничний випадок парамагнетизму. В системі, що складається з багатьох атомів або молекул, магнітні моменти яких зумовлені спінами електронів, діють якісь сили, які прагнуть однозначно орієнтувати спіни двох сусідніх атомів або молекул, тому в деяких речовинах виникають області, що мають внаслідок додавання спінів електронів значні магнітні моменти. Ці області називаються доменами – спіни, що об’єдналися. Кожен домен має магнітний момент, який дорівнює сумі спінів електронів. Якщо магнітного поля немає, то розподіл доменів має випадковий характер і сума магнітних моментів феромагнетика чисельно дорівнює нулю, як і у парамагнетиків.

В дослідах А. Ейнштейна і В. де Гааза було показано, що намагнічування феромагнетика обумовлено орієнтацією спінів електронів. Розглянемо схему одного з цих дослідів (рис. 5.2). Легкий феромагнітний стержень підвішений на кварцовій нитці. Цей феромагнітний стержень розміщений всередині соленоїда. Коли через соленоїд пропускали змінний електричний струм, стержень повертався то в одну, то в іншу сторону, залежно від напрямку струму. Поворот фіксується на шкалі за відхиленням променя, що відбивається дзеркалом.

Поворот стержня пояснюється тим, що електрон має не лише власний магнітний момент, а і механічний момент.

Якщо крізь соленоїд пропускати струм І, то внаслідок дії зовнішнього магнітного поля, магнітні моменти будуть розміщуватись впорядковано, що призводить до впорядкованого направлення моментів імпульсів.

Обчислення, які були проведені на підставі досліду, показали, що відношення магнітних моментів до механічного моменту відповідає не орбітальному руху електронів, а спіну електрона.

Уферомагнетиків магнітна проникність залежить від зовнішнього магнітного поля і тому є певна залежність між магнітною індукцією і напруженістю магнітного поля.

Усі магнетики можна поділити на слабо магнетики (діа-, пара-) та сильно магнетики (феромагнетики).Залежність намагніченості від напруженості поля показана на рис. 5.3.

Тоді можна сказати, що феромагнетики – це тверді речовини, які володіють спонтанною намагніченістю.

Типові представники феромагнетиків: залізо, кобальт, нікель та сплави.

Основна крива намагніченості показує залежність намагніченості від напруженості, або залежність магнітної індукції від напруженості магнітного поля.

Рис. 5.2

При невеликих значеннях напруженості намагніченість досягає насичення і магнітна індукція визначається за формулою:

.

Відповідно, магнітна індукція зростає зі збільшенням напруженості магнітного поля.

Рис. 5 3 Рис.5.4

Після досягнення стану насичення, магнітна індукція продовжує зростати зі збільшенням Н за лінійним законом:

,

.

У зв’язку з тим, що залежність В від Н є нелінійною, для феромагнетиків не можна ввести магнітну проникність як величину, що характеризує магнітні властивості даного феромагнетика, але вважають, що

.

При цьому магнітна проникність є функцією напруженості.

Якщо зобразити графік залежності магнітної проникності від температури, то магнітна проникність буде спочатку збільшуватись до деякого значення, а потім почне спадати (рис. 5.5).

Для феромагнетиків може досягати великих значень (наприклад для заліза – 5000).

Рис. 5.5

Поняття магнітної проникності використовується лише для основної кривої намагнічування, оскільки залежність магнітної індукції від напруженості неоднозначна.

5.5. Намагнічування і перемагнічування феромагнетиків. Точка Кюрі

Для феромагнетиків характерне явище магнітного гістерезисну.

Зв’язок між напруженістю Н і індукцією В, намагніченістю J і індукцією B є неоднозначним і визначається передісторією намагнічування феромагнетика.

Якщо спочатку не намагнічений феромагнетик намагнічувати, збільшуючи напруженість магнітного поля від нуля до значення при якому настає насичення, а потім зменшувати відН до –Н, то крива намагнічування В(Н) піде по шляху, який показано на графіку – A-C-K-D (рис. 5.6).

Якщо збільшувати напруженість від –Н до Н, то крива піде по шляху D-F-K₁-A. Отримаємо петлю гістерезисну.

Рис.5.6

Коли в точках A і D досягається насичення отримуємо петлю гістерезисну великого розміру. Коли Н=0 намагніченість не зникає, тобто маємо точку C, яка має значення якоїсь магнітної індукції B_r – залишкова магнітна індукція (або залишкова намагніченість).

З наявністю замкненого кола пов’язане існування постійних магнітів.

Величина напруженості, при якій В=0 – Нс – називають коерцитивною силою. Значення цієї сили є дуже важливим, бо за її значенням феромагнетики можна використовувати по-різному.

Щоб розмагнітити феромагнетик, потрібно його розмістити в котушці, по якій пропускають змінний струм і амплітуду постійно зменшувати до 0. Таким чином в феромагнетиках відбуваються багаторазові циклічні намагнічування, в яких петлі гістерезисну зменшуються, стягуючись до нуля, де Н=0.

При перемагніченні феромагнетики нагріваються. В одиниці феромагнетика виділяється теплота, яка чисельно дорівнює площі петлі гістерезису:

. (5.4)

Для феромагнетиків характерна температура Кюрі. При підвищенні температури вище точки Кюрі феромагнітні властивості зменшуються, тобто зменшується намагніченість насичення.

При даній температурі феромагнітні властивості зникають. Якщо далі підвищувати температуру, то феромагнетик перетвориться в парамагнетик.

Лекція 17