2.4. Розподіл молекул газу за енергіями

2.4.1. Закон розподілу Больцмана

Розглянемо розподіл мікрочастинок за енергіями на прикладі ідеального газу, що знаходяться в полі тяжіння: нехай сили поля напрямлені вздовж осі z.

Рис. 1

Тиск газу в різних точках вздовж цієї осі буде різним. Виберемо дві площини , причому. Ці площини орієнтовані перпендикулярно до осіz і знаходяться на відстані dz одна від одної. Якщо тиск газу на обох площинах буде чисельно дорівнювати p i p+dp, то різниця тисків dp чисельно дорівнює сумарній силі, що діє на частинки газу, що знаходяться в об’ємі даного паралелепіпеда з основою S і висотою dz відносно до площі даної основи:

,

n – концентрація молекул в даному об’ємі;

- сила, що діє на 1моль в точці з координатою z.

Дана сила пов’язана з потенціальною енергією молекули співвідношенням:

.

Таким чином, додатковий тиск dp чисельно дорівнює:

.

Приймаючи температуру ідеального газу у всіх точках однаковою, на основі рівняння Менделєєва-Клайперона, знаходимо, що:

.

Співставляючи два останні рівняння:

.

Проінтегрувавши і пропотенціювавши даний вираз, отримаємо:

. (1)

Рівняння (1) називають законом розподілу Больцмана.

В даному рівнянні іn- концентрації молекул газу в стані з відповідно прийнятою нульовою потенціальною енергією і деякою в стані 1.

Рівняння може бути отримане з більш загальних міркувань. Воно має універсальний характер, бо використовується для будь-яких систем з мікрочастинок, що знаходяться в різних потенціальних полях. Наприклад, для поля тяжіння Землі на великій висоті:

. (2)

Для двох різних станів з потенціальними енергіями , отримаємо:

. (3)

Так як тиск газу пов’язаний з концентрацією молекул рівнянням p=nkT, то на основі рівняння (2), запишемо:

. (4)

Тиск p і тиск :

- тиск на поверхні Землі;

p - на висоті z над Землею;

- молярна маса газу.

Рівняння (4) – барометрична формула.

2.4.2. Закон розподілу Максвела

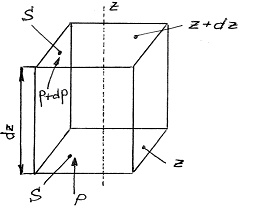
Рис. 2

Теплова або середня квадратична швидкість представляє собою середню характеристику теплового руху усієї сукупності мікрочастинок. В дійсності, всі мікрочастинки рухаються з різними швидкостями і можна поставити питання про розподіл мікрочастинок за швидкостями.

Максвел вирішив цю задачу про розподіл молекул ідеального газу за швидкостями постійного руху в стані теплової рівноваги. Він показав, що вірогідність того, що деяке число молекул dN із загального числа молекул N володіє швидкостями, що лежать у інтервалі від до. Виражається дана вірогідність відношенням:

, (5)

f(v) - функція розподілу молекул за швидкостями;

dv - інтервал швидкостей, що розглядається.

Вигляд функції можна встановити на прикладі руху молекул ідеального газу в однорідному полі тяжіння. Спочатку розглянемо закон розподілу молекул по значенням вертикальної складової швидкості. Число молекул , що знаходяться в безкінечно тонкому шарі газу на висоті z, товщина dz:

,

n(z) – концентрація молекул газу на висоті z.

Рухаючись як вільні, дані молекули через деякий інтервал часу перейдуть на висоту і займуть шар. При цьому, їх швидкості будуть лежати в інтегралі віддо, але одне і те ж число молекул. Якщо прийняти, що, то незмінність числа цих молекул виражається:

, (6)

- концентрація молекул газу на висоті .

При русі в полі тяжіння горизонтальні складові швидкості не будуть змінюватись, а змінавизначається законом збереження енергії, згідно якого:

.

Якщо продиференціювати це рівняння, при вибраних сталих значеннях , отримаємо:

.

За час dt молекула на висоті z пройде шлях , а на висоті, пройде шлях.

Якщо виключимо елементарний час dt, то:

. (7)

Перемножимо почленно рівняння (6) і (7) і знайдемо:

.

Із урахуванням останнього виразу, рівняння (5) спрощується і приймає вигляд:

.

Використовуючи закон Больцмана у вигляді рівняння (2), отримаємо:

.

На основі закону збереження і перетворення енергії, знаходимо, що:

.

Тоді:

Звідси слідує, що:

. (8)

В стані теплової рівноваги рух молекул газу буде рівновигідним по всіх напрямках.

Так як вірогідність складної події, яка складається з незалежних подій, рівна добутку вірогідностей цих подій, то повні функція розподілу молекул за швидкостями буде мати вигляд:

.

Тоді:

. (9)

З урахуванням рівняння (9), запишемо рівняння (5):

, (10)

- об’єми нескінчено малого паралелепіпеда, що побудований в координатній системі простору швидкостей навколо точки з векторною координатою .

Так як тепловий рух молекул газу рівновірогідний у всіх напрямках, для визначення відношення необхідно просумувати усі елементарні об’єми, що знаходяться на відстаніі ці об’єми заповнять шаровий прошарок між 2 нескінчено-близькими сферами з радіусамиv i v+dv.

Об’єм такого шару:

.

Таким чином, число молекул з швидкостями в інтервалі від v до v+dv буде чисельно дорівнювати:

, (11)

- деяка стала, що не залежить від швидкості молекул.

Знайдемо вираз величини А. Так як інтервал швидкостей від нуля до нескінченності охоплює всі молекули, то очевидно, що інтеграл:

,

тоді:

.

Якщо зробити заміну змінних і скористатися значенням, що, то знайдемо:

.

З урахуванням цього, закон розподілу Максвела:

. (12)

Графік функції рівняння (9) представляє собою Гаусову криву розподілу випадкової кривої:

Рис. 3

Густина вірогідності розподілу молекул по швидкостям буде мати вигляд:

Рис. 4

Як слідує з даного рівняння, при кожній температурі є деяка швидкість, яка має найбільше число молекул (цю швидкість називають найбільш вірогідною). Знайдемо вираз для цієї швидкості з урахуванням рівняння (12), дослідивши дане рівняння на екстремуми. Скоротивши в рівнянні (12) сталі величини і проінтегрувавши, отримаємо:

.

Звідси знаходимо вірогідну швидкість:

. (13)

Середня арифметична швидкість молекул:

.

Стан газу можна характеризувати однією з трьох швидкостей:

- вірогідною;

- середньою арифметичною;

- середньою квадратичною.

Наприклад:

p,V – тиск і об’єм.

Співвідношення між цими швидкостями:

.