6.2.2. Складання взаємно-перпендикулярних коливань

Нехай матеріальна точка приймає участь в двох взаємо перпендикулярних коливаннях:

- перше коливання , (1)

- друге коливання (2)

з однаковою частотою і різницею фаз(наприклад, коливання матеріальної точки відносно положення рівноваги в одному напрямі і коливання в напрямі, що перпендикулярний до першого). В даному випадку матеріальна точку буде рухатись по деякій криволінійній траєкторії, рівняння якої в параметричній формі виражається рівняннями (1) і (2). Якщо видалити з них часt, то отримаємо рівняння траєкторії, що виражається через різницю фаз . На основі рівняння (2) знаходимо:

.

Перенесемо перший доданок у ліву частину рівняння і піднесемо до квадрату ліву і праву частини, і отримаємо рівняння результуючого коливання:

. (3)

Рівняння (3) – рівняння еліпса, півосі А і В якого не співпадають з координатними осями x і y.

1.

.

Звідси маємо рівняння прямої:

. (4)

Тобто матеріальна точка рухається вздовж прямої, відстань її від початку координат . Тобто результуючий рух є гармонійним коливанням вздовж прямої рівняння (3) з деякою частотоюі амплітудою.

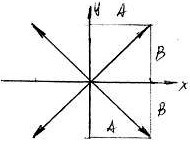
Рис. 3

2.

рівняння (3) прийме вигляд:

.

Результуючий рух буде представляти собою гармонічний рух вздовж прямої

(5)

Рис. 4

3.

рівняння (3) прийме вигляд:

. (6)

Рівняння еліпса, що приведене до координатних осей x і y. Напівосі еліпса А і В відповідно дорівнюють амплітудам коливань, якщо амплітуди коливань однакові – еліпс перейде у коло.

Випадки відрізняються лише напрямком руху по еліпсу, що витікає з рівнянь (1) і (2):

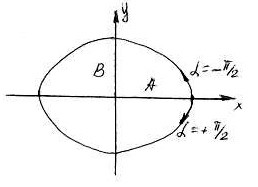
Рис. 5

Якщо частоти коливань відрізняються на досить малу частоту , то їх можна розглянути як коливання з однією частотою, але з повільно змінюючоюся різницею фаз. Тоді рівняння (6.2.1) і (6.2.2):

Результуючий рух в даному випадку буде відбуватися по змінній кривій, форма якої залежить лише від різниці фаз, що змінюються в межах . Якщо частоти відрізняються незначно, то траєкторія приймає вигляд фігур Лісажу. При відношенні частот

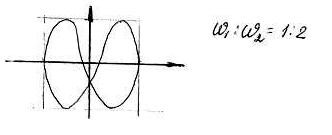
Рис. 6

Лекція 11

6.3. Згасаючі та вимушені коливання

6.3.1. Згасаючі коливання. Добротність

У будь-якої коливальної системи є сили, які перешкоджають коливальному руху, наприклад, сили тертя в точці підвісу маятника, сили опору навколишнього середовища, тощо. Результуючою всіх цих систем називається затримуючою силою. Дія цієї сили викликає постійне затухання коливань. При малих швидкостях руху тіла, що знаходиться в коливальному русі затримуюча сила пропорційна швидкості руху:

r- постійна величина для системи – коефіцієнт опору.

На систему діє квазіпружна та затримуюча сила, тоді другий закон Ньютона має вигляд:

. (1)

Поділимо на масу і отримаємо:

,

; ,

- коефіцієнт затухання.

Маємо рівняння затухаючих коливань:

, (2)

- величина власної частоти осцилятора.

Так як затримуюча сила викликає постійне зменшення амплітуди коливань (), тоді розв’язок рівняння (2) будемо шукати:

, (3)

- частота затухаючих коливань, .

Продиференціюємо рівняння (3) і підставивши значення у рівняння (2), отримаємо:

.

Дане рівняння виходить при будь-яких значеннях t, якщо один з коефіцієнтів при тригонометричних функціях дорівнює нулю, тобто:

, (4)

так як , то можна скоротити, тоді:

. (5)

З рівняння (4) знаходимо інші величини якщо , то,

. (6)

Із рівняння (6) знайдемо залежність амплітуди від часу:

.

Знайдемо вираз для частоти : з рівняння (4) знаходимо:

;

.

Підставляємо в рівняння (6.3.5) і отримаємо:

.

Звідси, скоротивши на А, маємо:

. (7)

Дане рівняння використовують для реальної системи при умові, що відношення , тобто.

При цих умовах, тобто при невеликому затуханні вільні затухаючі коливання описуються рівнянням:

. (8)

Графік даної функції має вигляд:

Рис. 1

При значенні t=0 початкове зміщення :

,

і початкова фаза задаються початковими умовами:

.

Період затухаючих коливань:

. (9)

Відношення значень амплітуд відповідає моментам часу, що відрізняються на величину періоду:

.

Це відношення – дикримент затухання, а логарифм даного відношення:

.

Це відношення – логарифмічний дикримент затухання.

Знайдемо деякий час , по закінченні якого амплітуда коливань зменшується вe=2,72 раз. Скористаємось формулою (6):

,

тому, що ,- час релаксації.

З урахуванням рівняння (10) знаходимо, що:

.

Число коливань () по закінченню яких амплітуда зменшується вe раз:

.

Величина

(11)

називають добротністю коливальної системи. Добротність пропорційна числу коливань, яке здійснює система за той час, по закінченню якого амплітуда зменшується в е раз.