6. Коливальний рух

Лекція 9

6.1. Вільні незгасаючі гармонічні коливання

6.1.1. Загальні відомості про коливання

Коливальним процесом називається усякий регулярний або майже регулярний процес, у якому усяка фізична величина набуває однакових або майже однакових значень через рівні або майже рівні проміжки часу.

Теорія коливань вивчає коливальні рухи різної фізичної природи загальними методами. Встановлені закономірності, які характеризують коливальний процес вцілому незалежно від природи фізичних величин, що здійснюють коливання.

Коливання виникають тоді, коли системі, здатній виконувати коливальний рух надається енергія. По фізичній природі коливання можуть бути:

1. механічні(коливання моста, корабля, маятника, струни, коливання густини повітря при розповсюдженні в ній хвиль);

2. електромагнітні(коливання напруженості електричного і магнітного полів в електромагнітних хвилях);

3. електромеханічні(коливання мембрани телефону);

4. хімічні(коливання концентрації реагуючих речовин при протіканні періодичних хімічних реакцій).

Швидкість зміни стану, що повторюється характеризується частотою коливань – кількість коливань за одиницю часу .

По механізму виникнення і протікання, коливання розділяються на вільні, вимушені, автоколивання.

Вільні коливання здійснює система, що представлена сама собі після порушення рівноваги дією зовні(математичний маятник).

Вимушені – коливання, що виникають в коливальній системі під дією змінної зовнішньої системи, наприклад, коливання механічних конструкцій під дією змінної сили.

Автоколивання – незатухаючі коливання, які можуть існувати в якій-небудь системі при відсутності змінної зовнішньої дії, причому амплітуда і період коливань відповідають властивостям самої системи, наприклад, маятник годинника, коливання струни смичкових інструментів.

По формі і характеру протікання коливання розділяються на прості і складні.

Простими є гармонічні коливання, що здійснюються за законом синуса або косинуса; ті, при яких фізична величина змінюється протягом часу за законом синуса або косинуса.

Гармонічні коливання займають важливе місце за двох обставин:

• у природі дуже часто зустрічаються коливання по формі, близькій до гармонічних коливань

• періодичні процеси іншої форми можуть бути представлені як накладання декількох гармонічних коливань

6.1.2. Вільні незгасаючі гармонічні коливання

Розглянемо систему, яка складається з кульки масою m і деякої пружини. В стані рівноваги на дану систему діє сила mg і тоді пружина отримає певне видовження.

Рис. 1

Сама сила mg врівноважена з силою пружини . Якщо змістити кульку від положення рівноваги на деяку відстаньx, то видовження пружини буде: .

Рис. 2

Проекція на вісь x результуючої на кульку сили буде дорівнювати:

. (1)

Коли , то сила:

. (2)

У даному випадку сила по своїй природі пружна і знак „-” вказує, що сила F направлена в сторону, яка протилежна до зміщення кульки від положення рівноваги.

Сила іншого коливання, яка має ту саму закономірність, що і пружина, називається квазіпружною і має такі властивості:

1. сила пропорційна зміщенню систем відносно положення рівноваги;

2. сила завжди направлена до положення рівноваги.

Розглянемо пружину так, щоб зміщення кульки відносно рівноваги дорівнювало якомусь значенню a. У цьому стані енергія системи складається із потенціальної енергії, що обумовлена додатковим розтягом пружини. Після цього предоставимо систему самій собі. Під дією сили F кулька рухається з прискоренням до положення рівноваги. При цьому потенціальна енергія пружини перетворюється у кінетичну енергію руху кульки.

В стані рівноваги на кульку не діє ніяка сила, тобто пружина повертається у свій початковий стан.

.

Потенціальна енергія розтягу пружини повністю перейшла в кінетичну і тому швидкість кульки стала максимальною. З положення рівноваги кулька буде рухатися вверх, зжимаючи пружину. Внаслідок цього на кульку діє сила F=-kx. Швидкість кульки буде зменшуватись, а її кінетична енергія буде перетворюватись в потенціальну енергію зжимання пружини.

В крайньому верхньому положенні швидкість кульки дорівнює нулю, і кінетична енергія повністю перетворюється в потенціальну енергію пружини.

Якщо на систему не діють ніякі сили, то під дією сили kx кулька буде здійснювати коливання від а до –а. Для даної системи другий закон Ньютона:

, (3)

.

Якщо розділити рівняння (6.1.3) на m, отримаємо:

; ;

. (4)

Це рівняння руху кульки під дією сили пружності.

Будь-яке тіло, що здійснює коливання згідно рівняння (4), називається лінійним гармонічним осцилятором.

Рішенням рівняння (4) є рівняння вигляду:

. (5)

Дане рівняння описує вільні незатухаючі гармонічні коливання. У рівнянні x – зміщення системи від положення рівноваги в момент часу t; А– амплітуда коливань; - кутова(циклічна) частота коливань;- фаза коливань;- початкова фаза коливань.

Час T, протягом якого система здійснює одне повне коливання, називається періодом коливань. Число коливань за одиницю часу – частота .

Кутова частота пов’язана з періодом і частотою:

,

1Гц – частота коливання, період якого дорівнює 1 сек.

Якщо рівняння (5) продиференціювати по часу, знайдемо швидкість і прискорення процесу:

, (7)

. (8)

Позначимо , тоді:

. (9)

Тобто швидкість та прискорення теж змінюються за гармонічним законом, причому швидкість випереджає переміщення по фазі на , а прискорення і переміщення знаходяться в протифазі.

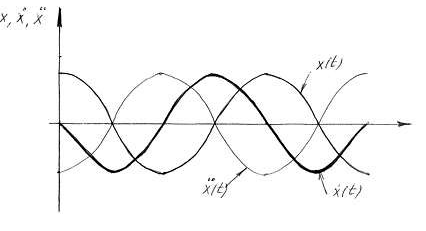
Рис. 3

Враховуючи співвідношення між частотами (6), систему (9) можемо записати:

. (10)