
- •ПРЕЗЕНТАЦИЯ ПО КУРСУ
- •Схема изучения дисциплины
- •ГИДРАВЛИКА
- •Силы, действующие в жидкости
- •Силы, действующие в жидкости
- •Силы, действующие в жидкости
- •Давление и его свойства
- •Свойства давления
- •Понятие о градиенте давления
- •Понятие о градиенте давления
- •Понятие о градиенте давления
- •Понятие о градиенте давления
- •Единицы давления
- •Вязкость жидкости
- •Вязкость жидкости
- •Вязкость жидкости
- •Вязкость жидкости
- •Идеальная жидкость
- •ГИДРАВЛИКА
- •Основное уравнение гидростатики
- •Закон Паскаля
- •Относительный покой жидкости
- •Относительный покой жидкости
- •Закон Архимеда
- •Закон Архимеда
- •Закон Архимеда
- •Изотермическая атмосфера
- •Неизотермическая атмосфера
- •Основные понятия кинематики жидкости
- •Основные понятия кинематики жидкости
- •Основные понятия кинематики жидкости
- •Уравнение неразрывности
- •Виды движения жидкости
- •Интегральная формула количества движения
- •Интегральная формула количества движения
- •Основы моделирования
- •Виды подобия. Масштабы моделирования
- •Виды подобия. Масштабы моделирования
- •Критерии подобия
- •Критерии подобия
- •Виды гидравлических сопротивлений
- •Формула Дарси-Вейсбаха
- •Местные гидравлические сопротивления
- •Местные гидравлические сопротивления
- •Местные гидравлические сопротивления
- •Местные гидравлические сопротивления
- •Местные гидравлические сопротивления
- •Кавитация
- •Истечение из насадков
- •Расчет короткого трубопровода
- •Расчет короткого трубопровода
- •Расчет короткого трубопровода
- •Расчет короткого трубопровода
- •Расчет короткого трубопровода
- •Расчет длинных трубопроводов
- •Гидравлический удар
- •Гидравлический таран

Критерии подобия
Критерий Фруда
Определяет отношение сил инерции к силам тяжестии
|
Fr = |
u2 |
= idem |
|
|
|
u2 |
|
= |
|
u2 |
|
|
gl |
|
|
|
í |
|
|
ì |
|
|||
|
glí |
|
glì |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||||||
При моделировании по Фруду |
|
ku = |
kl |
|
|
|
||||||
Вывод: Одновременно нельзя удовлетворить равенствотво критериевкритериев Рейнольдса и Фруда для одной и той же жидкости на моделимодели ии вв натуре.
Определяет отношение выталкивающей силы Архимедаеда кк силамсилам
инерции |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ar = |
gl ρ − ρ0 |
= idem |
|
glí |
ρí − ρí 0 |
= |
glì |
|
ρ ì − ρ ì 0 |
|
||||||
|
|
|
|
|||||||||||||
|
u2 |
|
ρ |
|
u 2 |
ρ |
í |
u |
2 |
|
ρ |
ì |
|
|||
|
|
|
|
|
|
|
í |
|
|
|
ì |
|
|
|
||
где ρ − ρ0 – отношение разности плотностей средыы ии струиструи кк
ρплотности среды.

Конечно-разностная формама уравнения Навье-Стоксаа
Напряженное состояние жидкости. Законы движения ии покояпокоя
жидкостей и газов основываются на законах механикии сплошнойсплошной среды, что позволяет рассматривать равновесие и течениеение жидкостижидкости вв целом без учета механизма молекулярного движения..
z |
z′ |
σ2 |
|
σ1 |
τ2 |
τ2 |
|
|
|||
τ1 |
τ1 |
x′ |
|
τ3 |
τ2 |
||
τ3 |
|||
|
τ1 |
|
|
|
τ3 |
x |
|
y′ |
σ3 |
||
|
|||
y |
|
|
На поверхностити гранейграней
элементарногого
параллелепипедапеда возникаютвозникают три различныхх попо величиневеличине касательных напряжениянапряжения ии тритри нормальных составляющихсоставляющих напряжений: вдольвдоль осейосей xx ии yy –– напряжение ττ11,, вдольвдоль осейосей xx ии
z – τ2 и вдоль осейосей yy ии zz –– ττ33..
Вдоль оси x действуетдействует нормальна я составляющаясоставляющая напряжения σσ1,1, вдольвдоль осиоси yy ––
σ2 и вдоль осии zz –– σσ33..
На массу жидкости, находящуюся в изолированном объемеобъеме,, действуют массовые силы, которые пропорциональныны третьейтретьей степени размера выделенного объема

Конечно-разностная формама
уравнения Навье-Стоксаа
Суммарная проекция силы, определяемая нормальнымими составляющими напряжения
|
σ + (∂σ |
∂x) dx dydz − σ dydz = ∂σ1 dxdydz. |
|||||||||
|
1 |
1 |
|
|
1 |
|
|
∂x |
|||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂τ3 |
|
|
|
|
|
|
Составляющие вдоль оси х |
|
dxdydz |
|
|
∂τ2 |
dxdydz |
|||||
|
∂y |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
∂y |
||
|
|
|
|
|
|
|
|||||
Суммарная составляющая сил, возникающих на граняхях изолированного элемента жидкости за счет дополнительногоельного напряжения в проекции на ось x, равна
∂σ + ∂τ3 + ∂τ
1 2 dxdydz
∂x ∂y ∂z
Аналогично составляющие дополнительного напряженияния,, действующие на остальных гранях, в проекциях на осии 00yy ии 00zz дадутдадут
составляющие сил: |
|
|
|
|
|
|
|
|
|
∂σ |
|
|
∂τ |
|
∂τ |
|
|
|
|
∂σ2 |
|
∂τ3 |
|
∂τ1 |
|
|
|
|
|
|
|||||||
|
|
+ |
+ |
dxdydz |
и |
|
|
3 |
+ |
1 |
+ |
|
2 |
dxdydz |
||||
|
|
|
|
|||||||||||||||
∂y |
∂x |
∂z |
∂z |
∂y |
∂x |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||

Конечно-разностная формама
уравнения Навье-Стоксаа
Прибавляя эти силы, отнесенные к единице массы жидкостидкости кк правойправой части уравнений Эйлера, получим условия динамическогокого равновесияравновесия в точке потока при течении реальной жидкости
|
∂ux |
|
|
|
∂ux |
|
|
|
∂ux |
|
|
∂ux |
|
|
1 ∂p |
|
1 |
|
∂σ1 |
|
|
∂τ3 |
|
|
|
|
|
∂τ2 |
|
|
|
||||||||||||||
|
|
+ ux |
|
+ uy |
|
+ uz |
= − |
|
+ X + |
|
+ |
|
+ |
|
|
|
dxdydz; |
||||||||||||||||||||||||||||
|
∂t |
∂t |
|
∂y |
|
ρ ∂x |
|
|
|
∂z |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
∂z |
|
|
|
ρ |
∂x |
|
|
∂y |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
∂uy |
|
|
|
∂uy |
|
|
|
|
∂uy |
|
|
|
∂uy |
|
|
1 ∂p |
|
1 |
|
|
|
∂σ |
|
|
|
|
∂τ |
|
|
|
|
|
|
∂τ |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
3 |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
+ ux |
|
|
|
+ uy |
|
|
|
|
+ uz |
|
|
|
= − |
|
|
+ Y + |
|
|
|
|
|
+ |
|
|
|
+ |
|
1 |
|
dxdydz; |
|||||||||||
|
∂t |
|
∂t |
|
|
∂y |
|
|
∂z |
ρ ∂y |
ρ |
|
∂y |
|
∂x |
|
∂z |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
∂uz |
|
|
|
|
∂uz |
|
|
|
|
∂uz |
|
|
|
∂uz |
|
|
1 ∂p |
|
1 |
|
∂σ3 |
|
|
∂τ1 |
|
|
∂τ2 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
+ ux |
|
|
|
+ uy |
|
|
|
+ uz |
|
= − |
+ Z + |
|
|
|
+ |
+ |
|
dxdydz. |
||||||||||||||||||||||||
|
∂t |
|
|
|
|
|
|
|
|
ρ ∂y |
ρ |
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
∂t |
|
|
|
|
∂y |
|
|
|
∂z |
|
|
|
|
∂z |
|
|
|
∂y |
|
|
|
|
∂x |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Определим теперь силы, возникающие в точке потокаа заза счетсчет вязкостивязкости..
Проекция на ось 0x сил вязкости, отнесенных к единицеице объемаобъема ии действующих в точке, определяемой в потоке координатамиинатами xx,, yy,, zz::
∂σ |
|
∂τ |
|
|
∂τ |
2 |
|
|
∂2u |
|
∂ |
∂uy |
|
∂u |
x |
|
|
∂ |
∂u |
|
∂u |
z |
|
||
1 |
+ |
|
3 |
+ |
|
+ μ |
2 |
|
x + |
|
|
|
+ |
|
|
+ |
|
|
|
x + |
|
|
|||
|
∂z |
|
|
∂x |
|
|
|
|
|
|
|||||||||||||||
∂x |
|
∂y |
|
|
|
∂x2 |
∂y |
|
∂y |
|
∂z |
∂z |
∂y |
||||||||||||

Конечно-разностная формама
уравнения Навье-Стоксаа
Дифференцируя уравнение неразрывности по x, получимчим
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂uy |
|
|
|
|
|
∂ |
|
∂u |
x + |
∂u |
z |
+ |
∂u |
|
= 0 |
|
|
∂ |
∂u |
|
= − |
∂ |
+ |
∂u |
||||
|
|
|
|
|
|
z |
или |
|
|
|
|
x |
|
|
|
|
z . |
||||||
|
|
|
|
|
|
|
|
|
∂y |
|
|||||||||||||
|
∂x |
∂x |
∂y |
∂z |
|
|
|
∂x |
∂x |
|
∂x |
|
∂z |
||||||||||
Тогда уравнение сил, возникающих за счет вязкости жидкостижидкости,, равноравно
|
2 |
u2x + |
2 |
u2x + |
2 |
|
|
μ |
∂ |
∂ |
∂ |
u2x |
|||
|
∂x |
∂y |
∂z |
|
|||
Аналогично в проекции на оси 0y и 0z дополнительнаяя проекцияпроекция силсил,, которые следует учитывать при течении вязких жидкостейостей,, составитсоставит::
|
∂ |
uy + |
∂ |
uy + |
∂ |
uy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
μ |
и |
μ ∂ |
uz |
+ |
∂ |
uz |
+ |
∂ |
uz |
. |
||||||||||||||||
|
2 |
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
∂x |
2 |
|
∂y |
2 |
|
∂z |
2 |
|
∂x |
2 |
|
∂y |
2 |
|
∂z |
2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||

Конечно-разностная формама уравнения Навье-Стоксаа
Уравнения Эйлера с учетом этих дополнительных силил примутпримут видвид::
|
∂ux |
|
|
|
|
∂ux |
|
|
|
|
∂ux |
|
|
|
∂ux |
|
|
1 ∂p |
|
μ |
|
2 |
ux + |
2 |
ux + |
2 |
ux |
|
|
|||||||||||||||||||||||||||||
|
|
+ ux |
|
+ uy |
|
+ uz |
= − |
|
+ X + |
|
∂ |
|
|
∂ |
|
|
∂ |
|
|
; |
||||||||||||||||||||||||||||||||||||||
|
∂t |
∂t |
|
∂y |
|
ρ ∂x |
ρ |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂z |
|
|
|
|
∂x2 |
|
|
|
∂y2 |
|
|
|
∂z2 |
|
||||||||||||||||||||||||||||||
|
∂uy |
|
|
|
|
∂uy |
|
|
|
|
|
∂uy |
|
|
|
|
∂uy |
|
|
|
1 ∂p |
|
μ |
|
2 |
uy |
|
|
|
2 |
uy |
|
|
|
2 |
uy |
|
|
||||||||||||||||||||
|
|
+ u |
|
|
|
+ u |
|
|
|
|
+ u |
|
|
= − |
|
+ Y + |
∂ |
|
|
+ |
∂ |
|
|
+ |
∂ |
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
x |
|
|
|
y |
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|||||||||||||||||||
|
∂t |
|
|
∂t |
|
|
|
∂y |
|
|
|
∂z |
|
|
|
ρ ∂y |
|
ρ |
|
∂x |
|
|
|
|
∂y |
|
|
|
|
∂z |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
∂uz |
|
|
|
|
|
∂uz |
|
|
|
|
|
∂uz |
|
|
|
|
∂uz |
|
|
1 |
∂p |
|
|
2 |
uz |
|
|
|
|
2 |
uz |
|
|
|
|
2 |
uz |
|
|
||||||||||||||||||
|
+ ux |
|
+ uy |
|
+ uz |
= − |
+ Z + μ |
∂ |
|
+ |
∂ |
|
+ |
∂ |
. |
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
∂t |
|
|
|
|
∂t |
|
|
|
|
|
∂y |
|
|
|
|
∂z |
|
ρ ∂y |
|
ρ ∂x |
2 |
|
|
|
|
∂y |
2 |
|
|
|
|
∂z |
2 |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
Полученная система уравнений называется уравнениямии НавьеНавье--СтоксаСтокса..
Уравнение Навье-Стокса, как и уравнение Зйлера, интегрируютсягрируются толькотолько для некоторых частных случаев, но в последние годы, в связисвязи сс
развитием различных методов решения подобных задачч,, полученныеполученные уравнения используются все чаще и являются идеальнымм инструментоминструментом,, позволяющим получить хороший результат. Наиболее частоасто длядля решения уравнений Навье-Стокса применяются численныеные методыметоды..

Общая схема применения численныхленных методов и их реализация наа ЭВМЭВМ
Под численными методами подразумеваются методы решениярешения задачзадач,, сводящиеся к арифметическим и логическим действиямям наднад числамичислами,, т.е. к тем действиям, которые выполняет ЭВМ.
Решение, полученное численным методом, обычно являетсяляется приближенным, т.е. содержит некоторую погрешностьость.. Источниками погрешности являются:
1)несоответствие математической задачи изучаемомуу реальномуреальному явлению;
2)погрешность исходных данных;
3)погрешность метода решения;
4)ошибки округлений в арифметических и других действияхйствиях наднад числами.
Погрешность в решении, обусловленная первыми двумяумя источникамиисточниками
называется неустранимой.
Численные методы в большинстве случаев сами по себебе являютсяявляются приближенными. Такие погрешности называются погрешностямирешностями
метода.

Общая схема применения численныхленных методов и их реализация наа ЭВМЭВМ
При решении задач на ЭВМ чаще всего встречаются дведве ситуацииситуации::
1)если количество выполняемых арифметических действиййствий невеликоневелико,, то, обычно, ошибки округления не проявляются, так каккак вв ЭВМЭВМ числачисла представляются с 10 и более десятичными значащимии цифрамицифрами,, аа окончательный результат редко бывает нужен более чемчем сс 55 десятичными значащими цифрами.
2)если задача сложная (уравнения с частными производнымиводными),), тото вв этом случае погрешности округления в каждом действиивии нене учитываются, так как они взаимокомпенсируются.
Численный метод может считаться удачно выбраннымм,, еслиесли егоего погрешность в несколько раз меньше неустранимой погрешностипогрешности,, аа погрешность, возникающая за счет округлений, называемаяваемая
вычисленной погрешностью, в несколько раз меньшее погрешностипогрешности
метода.

Общая схема применения численныленныхх
методов и их реализация наа ЭВМЭВМ
Этапы метода вычислительного эксперимента:
1.Формируется задача, выбирается физическая модельь процессапроцесса,, решается вопрос о том, какие физические величины надонадо учитыватьучитывать.. Проводится описание физической модели математическимеским способомспособом (дифференциальные, интегральные и другие уравненияния)).. Полученную математическую модель исследуют методамиодами математической физики, чтобы установить, правильноно лили поставленапоставлена задача, хватает ли исходных данных, не противоречатат лили ониони другдруг другу, существует ли решение поставленной задачи ии единственноединственно лили оно.
2.Построение приближенного численного метода решенияния задачизадачи,, тт..ее.. выбора вычислительного алгоритма. Вычислительныйй алгоритмалгоритм –– последовательность арифметических и логических операцийпераций,, припри помощи которых находится приближенное численноее решениерешение математической задачи, сформулированной на первомом этапеэтапе..
3.Программирование вычислительного алгоритма на ЭВМВМ..
4.Проведение расчетов на ЭВМ.
5.Анализ полученных численных результатов и последующееующее уточнениеуточнение математической модели.
Измерительные приборы, используемыеуемые припри проведении экспериментальныхх работработ
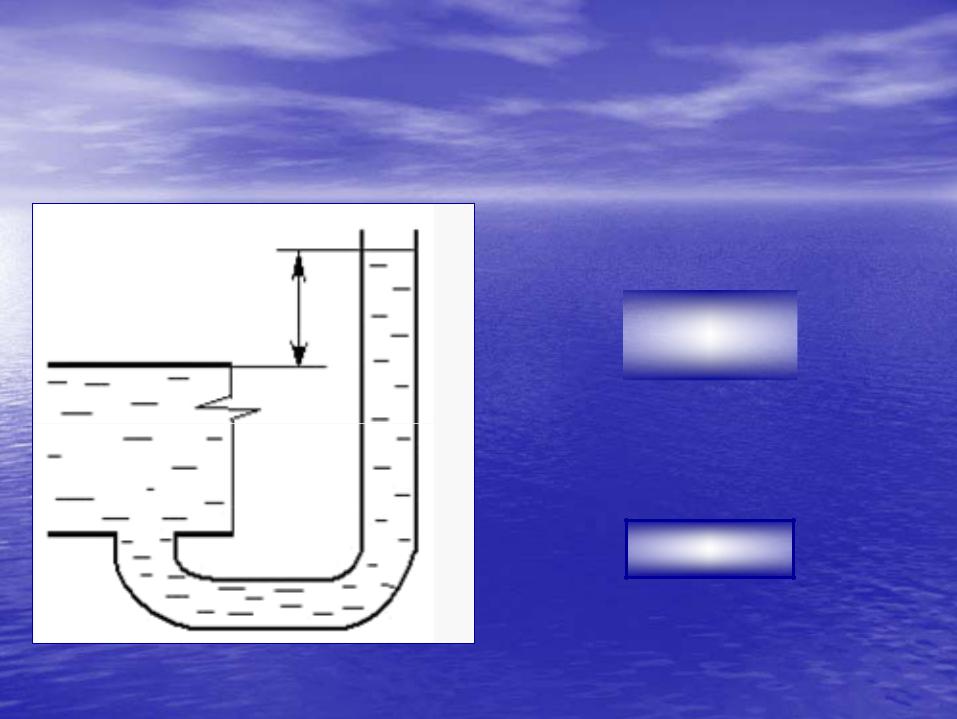
1. Жидкостные манометры прямого действияя..
Чувствительностьть манометраманометра B определяется по следующейследующей
формуле
H |
|
|
|
|
|
s = |
h |
= |
1 |
|
|
|
|
||||
p |
gρ |
|
|||
|
|
|
|
||
|
|
|
|
|
|
Давление определяетсяеляется попо
A разности уровнейй жидкостижидкости вв
трубках А и В
p = ρg h

Измерительные приборы, используемыеуемые припри проведении экспериментальныхх работработ
2. Механические манометры.
T |
Манометр состоит из согнутойнутой |
|
металлической трубки Т,, одинодин конецконец |
|
которой соединен с резервуаромрвуаром,, вв |
|
котором измеряется давлениеление.. КонецКонец |
|
трубки В соединен с рычагомагом ВСВС,, которыйкоторый |
|
поворачивает стрелку. Прири поворотеповороте |
B |
стрелки она указывает величинуеличину |
давления. При избыточномом давлениидавлении вв |
Cтрубке Т свободный ее конецонец ВВ начинаетначинает распрямляться и приводитит вв движениедвижение стрелку, которая показываетвает величинувеличину
давления. Такие манометрытры отличаютсяотличаются p прочностью.
Измерительные приборы, используемыеуемые припри
проведении экспериментальныхх работработ
R
H
V
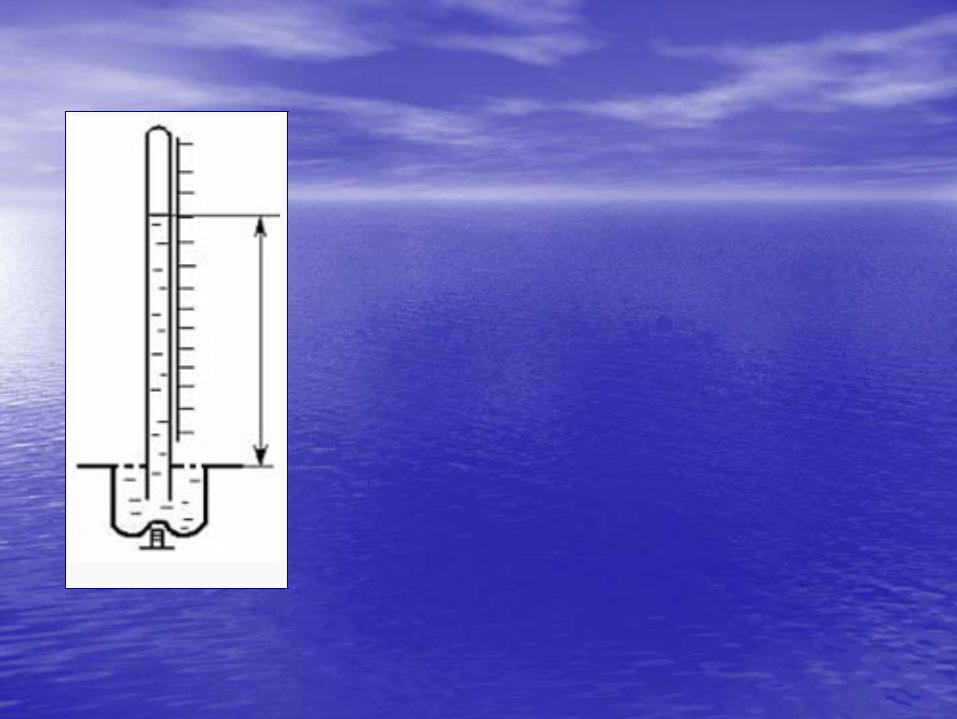
3. Барометры.
Барометры используются для измерениязмерения атмосферного давления. В лабораторныхраторных условиях используется барометрр ФортинаФортина,, позволяющий довольно точно измеритьизмерить атмосферное давление.
4. Вакуумметры.
Принцип действия механическогокого ии жидкостного вакуумметров аналогиченналогичен принципу действия механическогоского манометраманометра и жидкостного пьезометра.
Измерительные приборы, используемыеуемые припри
проведении экспериментальныхх работработ
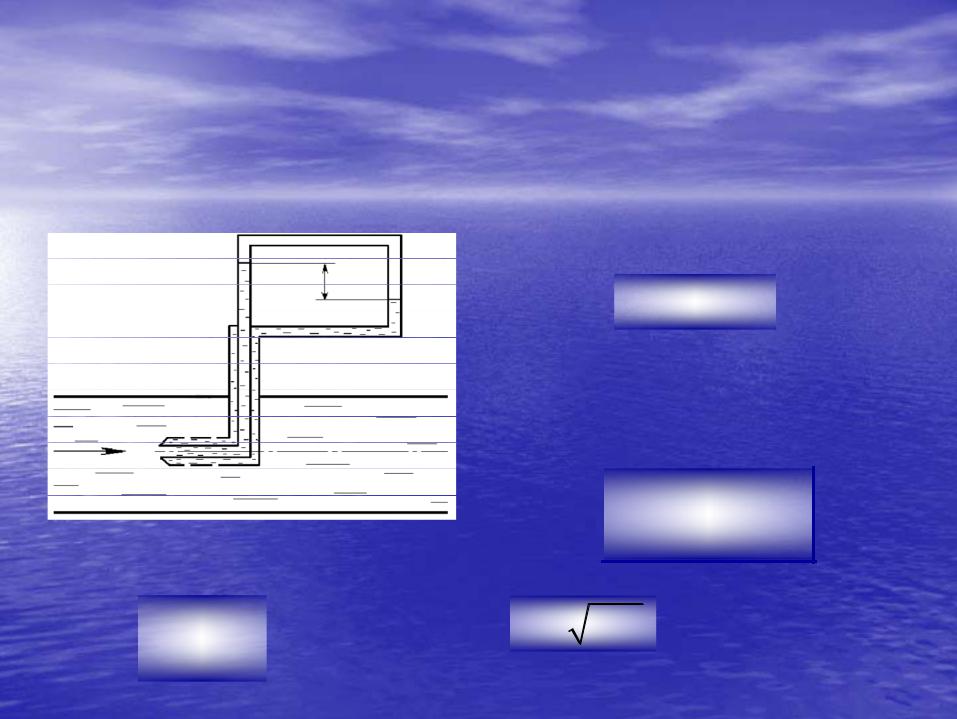
5. Трубка Пито–Прандтля.
Трубка Пито–Прандтля позволяет одновременно определитьеделить величинувеличину динамического и статического давления в определеннойной точкеточке потока.
|
|
|
|
|
|
|
|
|
Разность давления вв точкахточках АА′′ ии ММ′′ |
|||||||||
|
|
A′ |
|
|
|
|
|
|||||||||||
|
|
|
|
h |
|
|
будет |
|
|
|
|
|
|
|
||||
|
|
|
M′ |
|
p = ρgh |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
Разность давления |
pp зависитзависит отот |
||||||||
|
|
|
|
|
|
|
|
|
динамического давленияления нана входевходе вв |
|||||||||
|
|
M |
|
|
|
|
|
|
трубку Пито–Прандтлятля,, чточто следуетследует |
|||||||||
|
A |
|
|
|
|
|
|
из уравнения Бернуллиулли длядля точекточек АА |
||||||||||
|
|
M |
|
|
|
|
|
|
и М: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
pM = pA |
+ |
ρυ2 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. Таким |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
где υ – скорость потока на входе в трубку Пито–Прандтляля. Таким |
||||||||||||||||||
образом, |
|
2 |
|
|
откуда получаем |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
υ = 2gh. |
|
|
|
|
|
|
||||||||
|
|
p = |
ρυ |
|
|
|
|
|
|
|
|
|||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Измерительные приборы, используемыеуемые припри проведении экспериментальныхх работработ
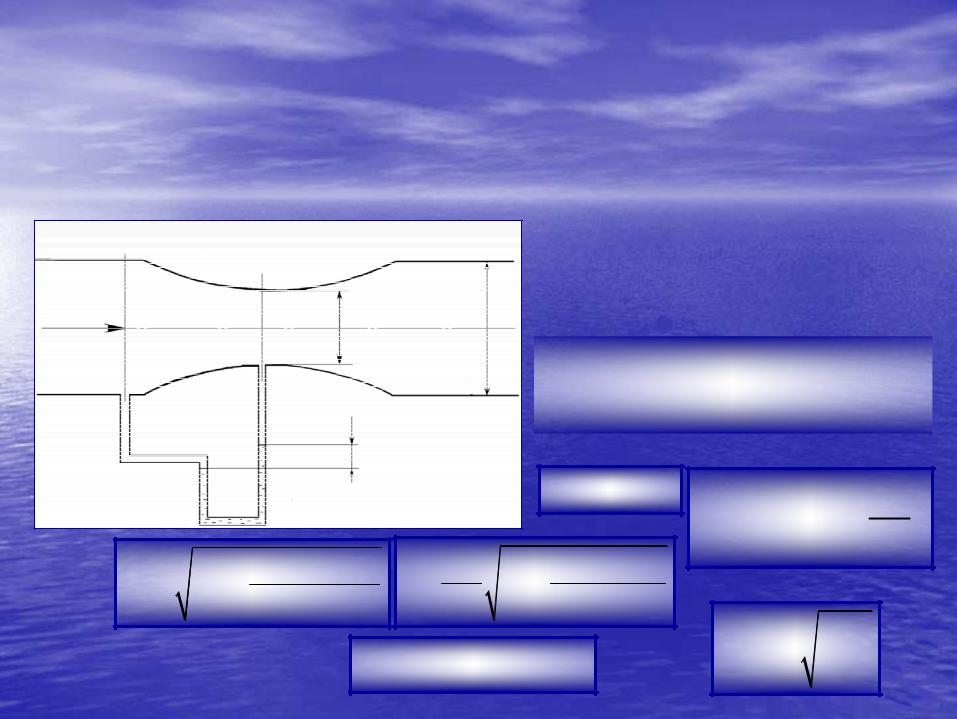
6. Расходомер Вентури.
Расходомер служит для измерения расхода жидкости ии представляетпредставляет собой плавную сходящуюся – расходящуюся вставку, кк которойкоторой подключается дифферциальный манометр.
1 |
|
Для вывода расчетнойчетной формулыформулы |
|
|
|||||
2 |
|
применим уравнениеение БернуллиБернулли длядля |
|||||||
d |
D |
сечения 1-1 передед сужениемсужением ии |
|
|
|
||||
сечения 2-2 в сужениижении ((αα11 == αα22 == 1)1).. |
|||||||||
2 |
|
|
|
|
|
|
|
|
|
|
υ22 |
− υ12 |
v22 |
|
υ12 |
|
|||
1 |
|
|
|||||||
|
|
p = ρ |
2 |
= ρ |
|
1− |
2 |
|
|
|
|
|
|
2 |
υ2 |
|
|
||
h |
|
С учетом уравненияения неразрывностинеразрывности |
|||||||
|
|
|
|
|
|
|
|
|
|
|
υ1S1 |
= υ2 S2 |
p = ρ |
2 |
|
− d |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
υ2 |
1 |
|
|
||
Откуда |
υ2 |
= |
2 |
p |
1 |
|
Q= |
πd |
2 |
2 |
p |
1 |
|
2 |
|
D4 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
ρ 1 |
− (d 4 |
/ D4 ) |
4 |
|
ρ 1−(d4 / D4) |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
2 |
p |
|
|
||||||
Для ртутного манометра |
p = (ρðò − ρæ )gh |
|
Q = Sμ |
|
|
|||||||||||||
|
|
|
ρ |
|
|
|||||||||||||
Измерительные приборы, используемыеуемые припри проведении экспериментальныхх работработ
F
FA
G
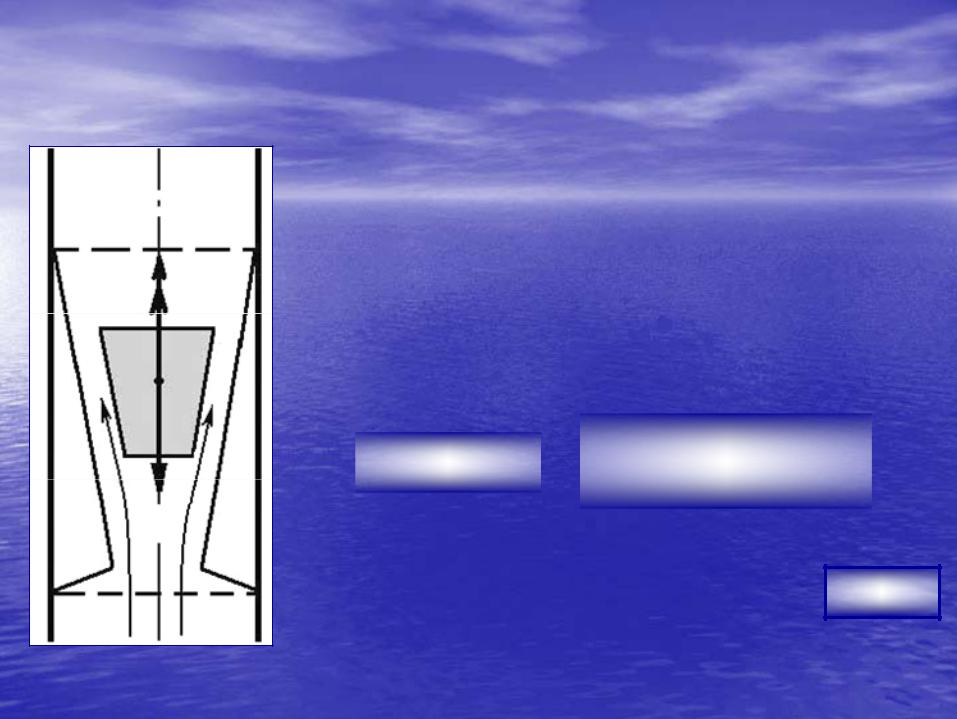
7. Ротаметры.
Ротаметры используются для измеренияерения расходарасхода жидкостей, имеющих слабые коррозийныерозийные свойства. Ротаметр состоит из сужающейсяжающейся стеклянной трубки и металлическогокого конусообразного измерителя. На измерительизмеритель действуют следующие силы: силаа тяжеститяжести GG,, архимедова сила FA, сила динамическогоческого давлениядавления жидкости F. Для измерителя, находящегосяодящегося вв покое, можно записать
|
|
|
ρæ υ2 |
|
G = F + FA |
|
mg = ρæVg + |
S |
|
|
2 |
|||
|
|
|
|
Сила тяжести и архимедова сила –– величинывеличины постоянные, поэтому сила динамическогоического давления жидкости при любом расходеасходе Q = υS
будет также постоянной.

Гидравлическиеие сопротивленияя
