4. Средняя хронологическая

Средняя хронологическая применяется когда значения признака Х заданы на несколько дат внутри периода. Формула средней хронологической простой:

(31)

где, n- число дат, на которые известны значения Х.

Средний уровень моментного ряда динамики с неравноотстоящими уровнями характеризуетсредняя хронологическая взвешенная, которая исчисляется по формуле:

(32)

где, X_i и X_i+1 – значение уровня моментного ряда динамики и уровня, следующего за ним;

f_i – промежуток времени между датами

Для изучения внутреннего строения совокупности применяют структурные средние - моду и медиану.

Мода ( ) - наиболее часто встречающееся значение признака в совокупности. В дискретном ряду мода определяется по наибольшей частоте. Для интервального ряда с равными интервалами мода определяется по формуле:

,

(33)

где - нижнее значение модального интервала (имеющего наибольшую частоту);

- ширина (шаг) интервала;

- частота модального интервала;

и - соответственно: частота интервала, предшествующего (последующего) модальному.

Медиана () - середина ранжированного ряда, т.е. величина признака, делящая ряд на две равные части. Для дискретного с нечетным числом уровней медианой будет варианта, находящаяся в середине ряда:

,

(34)

где – номер медианы.

Для дискретного ряда с четным числом медианой будет средняя арифметическая из двух вариант, расположенных в середине ряда:

.

(35)

Для интервального вариационного ряда медиана определяется по формуле:

,

(36)

где - нижняя граница медианного интервала;

- его величина; - его частота;

-сумма накопленных частот в интервалах, предшествующих медианному;

- сумма частот ряда.

Не каждая средняя величина является объективной характеристикой изучаемой совокупности. Для расчета типичности средней, колеблемости признака применяются показатели вариации.

Показатели вариации

Колеблемость, изменяемость величины признака у единиц совокупности называется вариацией.

Для характеристики вариационного ряда рассчитываются показатели вариации:

1. Размах вариации (R) - разница между наибольшим и наименьшим значением признака

(37)

2. Среднее линейное отклонение ( d ) - средняя арифметическая из абсолютных значений отклонений вариант от средней величины:

• простое

(38)

• взвешенное

(39)

3. Наиболее распространенным показателем вариации является среднее квадратическое отклонение .

,

(40)

где - дисперсия изучаемого признака в изучаемой совокупности. Дисперсиярассчитывается как база исчисления.

простая ,	(41)
взвешенная	(42)

Дисперсия – это средняя из квадратов отклонений вариант от средней. Она не имеет единиц измерения. Среднее квадратическое отклонение имеет ту же единицу измерения, что и значение Х и показывает, как в среднем конкретные значения Х отклоняются в ту или иную сторону от среднего значения:

Чем больше отклонение, тем менее типична средняя.

4. Коэффициент вариации характеризует колеблемость признака, однородность (неоднородность), совокупность, типичность (нетипичность) средней величины.

%,

(43)

Если коэффициент вариации менее 10% - вариация слабая, совокупность однородная, средняя типична.

Если коэффициент вариации находится в пределах от 10 до 33% - вариация умеренная, совокупность однородная, средняя типична.

Если коэффициент вариации находится в пределах от 33 до 60% - вариация признака сильная, совокупность не однородная, средняя не типична.

Если коэффициент вариации от 60 до 100% - вариация очень сильная, совокупность качественно неоднородная и средняя не является типичной характеристикой совокупности.

Для расчета показателей вариации используют вспомогательную таблицу.

Таблица 1. Расчет показателей вариации

Интервал	Частота	Расчетные показатели
		Середина интервала

Для характеристики ряда распределения рассчитывают:

• коэффициент асимметрии

  ;

  (44)

• коэффициент эксцесса

,

(45)

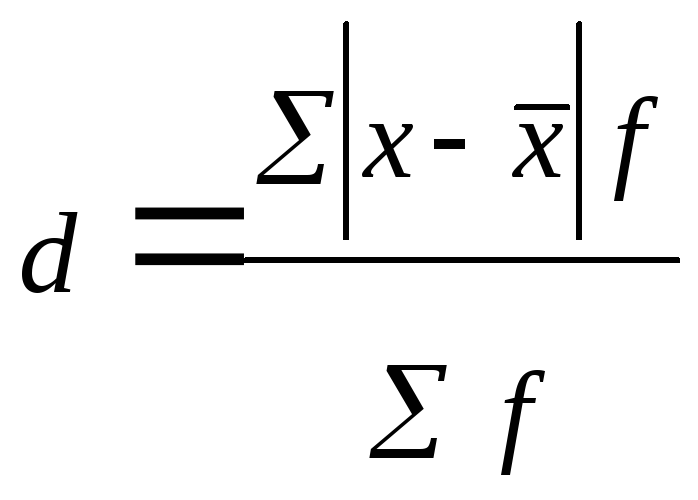
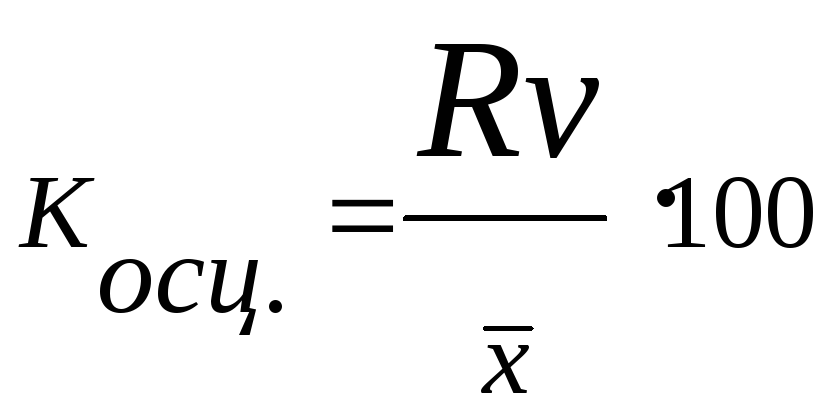где, (46) коэффициент осцилляции отражает относительную меру колеблемости крайних значений признака вокруг средней величины % (47)