Логическая семантика (сборник статей)

Таким образом, сутью программы Гильберта, в интерпретации Елены Дмитриевны, является доказательство того, что классическая математика является консервативным расширением финитной арифметики. В самом деле, если S и Ф суть системы с обычным синтаксисом, и если язык системы S является расширением языка системы Ф, то, как показывает Елена Дмитриевна, «доказательствонепротиворечивостисистемыSможетотождествляться с доказательством устранимости относительно Ф в том и только том случае, если система Ф полна и непротиворечива» [5, с.238]. Гильберт, по-видимому, был убежден, что финитная арифметика полна и сохраняет свою полноту при формализации. Однако Гёделем была доказана неполнота формальной арифметики, что делает программу Гильберта неисполнимой. Если система неполна, то и при условии непротиворечивости Ф нет оснований полагать, что S является консервативным расширением Ф, даже если S будет непротиворечива относительно Ф.

Итак, гильбертовская программа редукции терминов, относящихся к сильным абстракциям и идеализациям, несмотря на всю свою«гибкость»,оказаласьстольженеосуществимой,какипрограммы редукции теоретических терминов в логическом позитивизме. Это ставит вопрос о том, какой интерес может представлять сейчас обращение к программе Гильберта. С подобным вопросом мне приходилось сталкиваться при чтении лекций по философии науки аспирантам технических специальностей: зачем, восклицают слушатели, нам рассказывают о программе, которая все равно оказалась невыполнимой? Интересный ответ я нашла в той интерпретации программы Гильберта, которую предлагает Елена Дмитриевна: «Результаты Гёделя действительно показывают, что обоснование математики невозможно в рамках финитной математики Д. Гильберта. С философской точки зрения это свидетельствует о невозможности обоснования всей математики в рамках последовательного номинализма. Вся осмысленная математика несводима к высказываниям о конкретных, обозримых, реализуемых в пространстве объектах. … Таким образом, философский аспект проблемы обоснования математики вновь восстанавливает свое значение»[5, с. 242-243].

Теперь мне хочется поразмыслить над тем, каким именно образом может выступать этот философский аспект обоснования математики. И тут прежде всего надо отметить обстоятельство, котороевыпуклопоказываетинтерпретацияЕленыДмитриевны:

91

из невыполнимости программы Гильберта следует, что сильные теоретико-множественные понятия, актуальная бесконечность, не являются простыми «способами речи». Они играют продуктивную роль. А поскольку семантика существенно использует теоретико-множественные понятия, актуальную бесконечность, отсюда следует невозможность редуцировать семантику к конструктивным синтаксическим рассмотрениям. Такой важный урок можно извлечь из неосуществимости программы Гильберта. Поэтому Елена Дмитриевна, как мне представляется, вообще склонна интерпретировать ограничительные теоремы в положительном ключе, видя в них в первую очередь не свидетельства «бедности» стандартных формальных систем, а свидетельства «богатства» семантических понятий, которые требуют для своего выражения более сильных средств[5, с.123].

Ну, а как же быть с «заградительными мерами», требующимися при использовании сильных абстракций и идеализаций[5, с.265], чтобы гарантировать отсутствие парадоксов? Такие меры

вряде разделов математики реально функционируют. Елена Дмитриевна в этой связи придает большое значение конструктивным расширениям финитной точки зрения [5, с. 242-245, 267-268], которые позволяют построить доказательство непротиворечивости теории чисел. Упомянутые доказательства уже не означают устранимости, однако могут выступать гарантией от появления парадоксов, хотя и не настолько абсолютной, как это представлялось Гильберту. Набор средств, признаваемых финитными, при этом расширяется по сравнению с теми, которые признавалфинитнымисамГильберт,желавшийвидетьихабсолютно надежными и очевидными. С одной стороны, «существенно расширяется понятие системы реальных предложений математики, системы Ф. Под системой Ф понимается некоторая «приемлемая» система мышления, предложения которой рассматриваются как осмысленные предложения математики, несмотря на то, что

вних могут использоваться абстрактные понятия, относящиеся к идеальным конструкциям «второй и более высокой ступени»» [5, с. 243]. Отмечу, что такое движение методологической мысли

вматематике напоминает движение, которое вынуждены были проделать логические позитивисты, ослабляя требования к протокольным предложениям, отчего они становились не столько самоочевидными данными, сколько принимаемыми по соглашению. Недаром Р. Карнап в своей поздней работе писал: «Для

92

физика «наблюдаемое» … относится ко всем количественным величинам, которые могут быть измерены сравнительно простым, непосредственным путем. ...величины, которые могут быть найдены с помощью относительно простых процедур – длина с помощью линейки, время – часов, частота световых волн – спектроскопа – называются наблюдаемыми» [2, с.301-302]. С другой стороны, происходит существенное расширение той системы, средствами которой доказывается непротиворечивость S [5, с. 244]. Используется трансфинитная индукция. Это сильная абстракция, которую, поскольку она сама используется при доказательстве непротиворечивости формализованной арифметики, уже нельзя рассматривать как «способ речи». В то же время, математическое сообщество признает такой способ рассуждения конструктивным.

В использовании трансфинитной индукции, более сильной, чем финитные способы рассуждения и неформализуемой в формализованной арифметике, для обоснования этой последней, можно, как мне кажется, увидеть некоторую аналогию с изменениями в программе логического позитивизма по мере ее ослабления, размывания и замещения постпозитивистской философией. Если для логического позитивизма стояла задача определения теоретических терминов в терминах наблюдения, то постпозивизм, напротив, рассматривает термины наблюдения как определяемые на основе теоретических. Этими аналогиями мне хотелось бы подчеркнуть, что при конструктивном расширении финитных способов рассуждения гильбертовская программа видоизменяется. С одной стороны, построение доказательств непротиворечивости формальной арифметики на базе более сильных, чем мыслилось Гильбертом, средств, позволяет говорить о том, что «заградительные меры» все-таки действуют. На это обращает особое внимание Елена Дмитриевна. Но, с другой стороны, имеющиеся доказательства непротиворечивости уже не позволяют говорить об элиминируемости идеальных объектов и предложений о них. Они остаются необходимыми. Об их необходимости свидетельствуют «оценки роста длины вывода при устранении идеальных понятий, подтвердившие прозрение Гильберта о необходимости идеальных объектов и понятий для практического получения реальных результатов. По сравнению с такими оценками даже башня из степеней двоек растет слишком медленно … Методами формализма установлены оценки роста

93

сложности конструкций при понижении уровня используемых идеальных понятий и их сокращения при повышении абстрактности понятий … путь к новым полезным результатам проходит через сущности высших порядков, не имеющие никакой прямой связи с практикой» [4, с. 1095-1096].

Такилииначе,теориямножеств,хотяиограниченнаяпосравнению с наивной канторовской, но все равно использующая допущение актуальной бесконечности, активно используется, хотя доказательств непротиворечивости для имеющихся в современной математике аксиоматических формулировок теории множеств нет. Представляется, что в «постгёделевской» литературе по философии математики возобладал прагматический подход, для которого любые аксиомы, схемы рассуждений, абстракции оправдываются практикой своего применения. Если их использование удобно, продуктивно и достаточно долго не приводит к противоречиям, то от таких аксиом или абстракций никто, включая интуиционистов, всерьез отказываться не собирается. Насколько я могу судить, с недостижимостью идеала абсолютного обоснования математики (которым вдохновлялся Гильберт) все смирились, да и сам идеал вышел из моды. И здесь мы можем возвратиться к тому, с чего начиналось наше рассуждение — с утверждения Гильберта о том, что в математике существуют два типа предложений. Как мне кажется, для Елены Дмитриевны, в этом утверждении проглядывает указание на некий глубинный факт относительно человеческих познавательных способностей, заключающийся в том, что даже априорное познание нельзя свести к одному источнику, объять какой-то одной характеристикой. Потому-то идеи Канта и Гильберта интереснее для нее, чем логицизм Фреге и Рассела. Соответственно, нельзя свести

кодной характеристике сущность математики. Ее невозможно представить ни как целиком состоящую из аналитических истин, ни как всецело результат чистого созерцания.

Размышляя дальше над этой позицией, хочу сказать, что сущность математики, по-видимому, нельзя свести целиком ни

кинтуиции или конструктивным процедурам, ни к теоретикомножественным понятиям. Получается, что математика по своей сущности неустранимо двойственна. (Впрочем, может быть, и

тройственна,идажеболеетого,нопокрайнеймередвойственна.) Эта двойственность уходит корнями в использование двух рядов представлений (или интуиций): «С самых первых шагов в сфере

94

математической деятельности люди столкнулись с двумя рядами качественно различных представлений. С одной стороны, явления объективной действительности выступали как дискретные и неразложимыедалееиндивидуальныеобъекты–объектысчета...

Сдругойстороны,определеннаясовокупностьявленийвыступала в качестве непрерывных, делимых сколь угодно далеко однородных объектов. ... С самого начала возникновения математики как науки в ней существовали два основных направления исследований – арифметическое и геометрическое. Их сосуществованиебылоотнюдьнемирным;междунимипроисходиладовольно напряженная борьба...» [3, с. 34]. На первом ряде представлений основаны идея натурального числа, процедур, алгоритмизируемых подобно процедуре порождения натурального числа, следующего за любым данным, и идея конструктивных, построяемых объектов. На представлениях второго ряда – идея континуума. Если вспомнить Канта, то для него математика основывалась на двух типах чистого созерцания – времени и пространства.

Усилия ведущих математиков XIX века были направлены на редукцию этой двойственности посредством арифметизации математическогоанализа,т.е.устранениеапелляцийкгеометрической интуиции непрерывности. Из подобных усилий по созданию арифметической теории континуума выросли и канторовская теория множеств, и определение числа по Фреге и Дедекинду. При этом, представление континуума как точечного множества, дедекиндово определение действительного числа, не говоря уже о канторовой теории множеств существенно использовали понятие актуальной бесконечности и неконструктивные утверждения о существовании. Двойственная природа математики, таким образом, не была преодолена. Только теперь она предстала как двойственность потенциальной и актуальной бесконечности, конструктивного и неконструктивного. В этой ситуации Гильберт и выдвинул свою программу, стремясь показать, что сильные теоретико-множественные понятия являются не более чем «способом речи». Судьба гильбертовской программы показывает, что двойственность неустранима, хотя может принимать разные облики. Представляется, что упомянутая двойственность непосредственно касается соотношения логической семантики и синтаксиса. Логика также не сводима к одному знаменателю. Она тоже представляет собой соединение противоположных подходов: конструктивного (синтаксического) и неконструктив-

95

Семантические

основания

неклассических

логических

систем

97

Смирнова Е.Д.

Семантическиепредпосылки паранепротиворечивыхлогик

(Обоснованиепаранепротиворечивыхлогик ианализпротиворечий)1

I consider paraconsistent logic, taking an analysis of contradictions as a starting point. In so doing, a discrete role of the negation treatment is clarified with the help of the generalized approach to the construction of formal semantics (cf. [4]). It allows developing a paraconsistent logic on the base of semantical consideration, which makes it possible to enucleate conceptual and ontological prerequisites for contradictions to emerge.

Ключевые слова: паранепротиворечивая логика, противоречия, парадокс, дескрипция, семантика, онтология.

При рассмотрении паранепротиворечивых логик возникают два пути, два подхода к их анализу и обоснованию. В одном случае задача сводится к чисто формальным, синтаксическим преобразованиям логических систем: введение (исключение) определенных аксиом и правил вывода. Вторая линия связана с содержательным истолкованием оснований паранепротиворечивости, выявлением ее условий. При этом существенную роль играет анализ противоречий, их видов, истоков их возникновения. Важно установить, в каких случаях, при каких предпосылках, из противоречий следуют произвольные высказывания («что угодно»), а в каких – нет.

Прежде всего, необходимо четко различать противоречия онтологического плана, относящиеся к миру, и вопросы их репрезентации в языке, в «металогике». Одно дело – если в мире принимаютсяпротиворечивыеположенияделвдухе,например,«воображаемого мира» Васильева, другое дело – их рассмотрение в логике и соблюдение законов «металогики». И о «нелогичном» мире, мире «Страны чудес» Алисы, можно рассуждать логично, не нарушая принципов логики, не получая «что угодно». При-

1 Работа выполнена при поддержке РГНФ, грант №10-03-00570а

98

мем, что в случаях произвольных, «нелогичных» рассуждений оправдано получать произвольные, необоснованные утверждения.

Возникает вопрос, приводит ли принятие «противоречивого» мира, объекты которого наделены несовместимыми признаками, к логическим противоречиям (и в каких условиях).

Допустим, в мире допускаются положения дел S есть Р и S не есть Р – предметы необычного мира допускают «противоречивые» положения дел: объекты обладают и не обладают определенными свойствами или обладают несовместимыми свойствами. Высказывания о такого рода положениях, например в форме категорических высказываний вида А и Е, не контрадикторных, хотя они не могут быть вместе истинны – в силу объективных отношений между объемами понятий S и Р. Их утверждение не нарушает логики – мы не утверждаем и отрицаем то же самое в том же отношении в то же время.

Другое дело – утверждения вида «S есть Р» и «Неверно, что S есть Р», т.е. ¬(S есть Р), нарушается принцип непротиворечия: мы рассуждаем «нелогично», утверждаем нечто и отрицаем то же в том же смысле. В таком мире «произвольной логики» можно, естественно, получать «что угодно». В первом же случае положения дел несовместимы, но мы не нарушаем логических принципов.

В анализе противоречий особую роль играет трактовка отрицаний высказываний. Рассмотрим суждения логического вида Р(х). Обозначим (х) отрицание такого рода суждений в смысле: объект не обладает соответствующим свойством Р. В случае сингулярных термов контекст имеет вид В(( х)С(х)), получаем фактически два вида отрицаний исходного суждения (в зависимости от области действия дескрипции):

1. В(( х)С(х)) =Df !хС(х) & х(С(х) В(х))

2. [( х)С(х)]((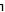х)С(х)) ≡ !хС(х) & х(С(х) (х)) «Нынеш-

ний король Франции не лыс», например

3. [( х)С(х)]¬ В(( х)С(х)) ≡ ¬( !хС(х) & х(С(х) В(х))) «Не-

верно, что нынешний король Франции лыс».

Если дескрипция пуста или не отвечает условию единственности, высказывания 1. и 2. оба ложны, но логический принцип

99

исключенного третьего не нарушается. Высказывания не контрадикторные. Если первый конъюнкт истинен, то истинность или ложность высказываний 1. и 2. зависит от того, обладает ли объект свойством В. Высказывания 1. и 2. не могут быть оба истинны – В(а) и (а) не могут быть вместе истинны, т.к. объект не можетобладатьинеобладатьсвойствомВ–вобычномпринима- емом мире (в отличие от «воображаемого»). Но речь идет в этом случае об онтологической непротиворечивости фактически.

Вслучае отрицания 2. принятие 1. и 2. не ведет к произвольным высказываниям, оно лишь утверждает в данном контексте противоречивость рассматриваемогомира.Мы мыслимлогично, не нарушая логического принципа непротиворечия, что имеет место в случае отрицания 3. Высказывание 3. отрицает то, что утверждалось в 1., 1. и 3. имеют вид: А и ¬А.

Именно контекстуальное определение дескрипций, учет областей действия дескрипций показывают различный смысл отрицаний (х) и ¬В(х). Если мы утверждаем и отрицаем то же самое, в том же отношении, – 1. и 3., – то в такой «логике» не удивительно получать произвольные утверждения. (Аналогично обстоит дело в случае простых собственных имен объектов).

Вслучае отрицания вида (а) ситуация напоминает онтологию мира Трактата Витгенштейна – введение «позитивных» и «негативных» фактов. Факт (Sachverhalt) это то, что «проецируется» атомарным предложением – положение дел, составляющее смысл предложения [1, 3.11]. Факты мира задаются атомарными высказываниями, «проецируются» ими. Отсутствие соответс-

твующей ситуации – это тоже факт мира, негативный факт . (В нашей нотации – это не отрицание «¬»). «Существование или несуществование атомарных фактов (Sachverhalt) есть действительность. (Существование атомарных фактов мы называем положительным фактом, несуществование – отрицательным)» [1, 2.06].

В описаниях состояний в качестве отрицаний высказываний фактически используется отрицание . Описания состояний задают «эмпирию», наличие (отсутствие) соответствующих положений дел – по сути те же «позитивные» и «негативные» факты в духе Трактата Витгенштейна.

100