48.1. Двухфазное короткое замыкание

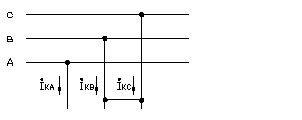
Запишем систему уравнений связывающих симметричные составляющие токов и напряжений, а также граничные условия в месте КЗ:

(48.1)

(48.2)

(48.3)

(48.4) 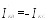(48.5) (48.6)

Если место КЗ не связано с землей, то ток нулевой последовательности равен 0, а из (48.3) следует

,

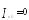Приняв фазу А за расчетную, воспользуемся формулами симметричных составляющих. Запишем уравнения для симметричных составляющих токов.

(48.7)

(48.8)

(48.9)

Из уравнений (48.8) и (48.9) следует

Вывод 1.

Запишем уравнения для симметричных составляющих напряжений: (48.10)

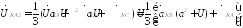(48.12)

Из уравнений (48.11) и (48.12) следует

Вывод 2.

Из уравнений (48.1) и (48.2) запишем выражения для определения напряжений прямой и обратной последовательностей:

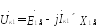
На основании вывода 2 можно прировнять правые части этих уравнений:

С учетом вывода 1

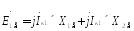
После простых преобразований получим:

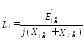
Действующее значение тока прямой последовательности

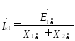
Действительные токи поврежденных фаз в месте КЗ легко можно выразить через

, т.е.

,

.

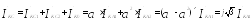Фазные напряжение в месте КЗ составляют:

,

,

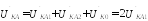Построим векторную диаграмму напряжений, а затем токов.

Из вывода 2 Из вывода 1

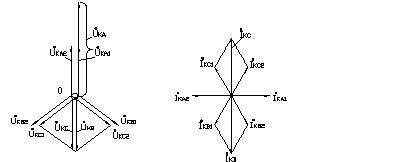
Векторная диаграмма напряжений Векторная диаграмма токов

48.2 Однофазное короткое замыкание

Система уравнений, связывающая симметричные составляющие токов и напряжений, и граничные условия в месте КЗ:

(48.13)

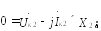(48.14)

(48.15)

(48.16) (48.17)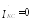 (48.18)

Уравнения для симметричных составляющих токов с учетом (48.17), (48.18):

Откуда следует:

Вывод 1.

С учетом (48.16), напряжение фазы А в месте КЗ будет равно:

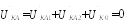
Откуда имеем:

Вывод 2.

Или, подставив сюда вместо симметричных составляющих напряжений их выражения из (48.13), (48.14), (48.15) и учтя вывод 1, получим после некоторых преобразований:

.

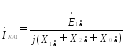Модуль тока прямой последовательности будет

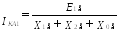
Ток в поврежденной фазе в месте КЗ:

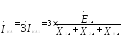
Этот же ток в соответствии с выводом 1 является током, поступающим в землю в месте замыкания, т.е.

Симметричные составляющие напряжений в месте КЗ:

из (48.13) следует:

из (48.14):

из (48.15):

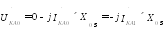
Напряжение можно записать по-другому:

Фазные (относительно земли) напряжения в месте КЗ:

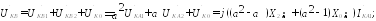
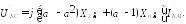
Построение векторных диаграмм токов и напряжений.

Из вывода 2 Из вывода 1

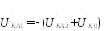
Векторная диаграмма напряжений Векторная диаграмма токов

Угол θ между напряжениями неповрежденных фаз зависит от соотношения между Х_2∑ и Х_0∑. Он изменяется в широких пределах 60º≤ θ ≤180º. Нижний предел соответствует условию Х_0∑=∞; к верхнему пределу θ стремится при Х_0∑→0. Лишь при Х_2∑= Х_0∑ угол θ=120º.

48.3 Двухфазное кз на землю

_{Система уравнений для симметричных составляющих токов и напряжений, и граничные условия в месте КЗ:}

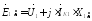_(48.19)

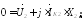_(48.20)

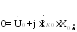_(48.21)

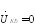_(48.22)

_(48.23)

_(48.24)

Для двухфазного КЗ на землю самоочевидные условия такие же, как и для однофазного, с той лишь разницей, что токи и напряжения поменялись местами.

Из разложения на симметричные составляющие выражения для напряжений нулевой, прямой и обратной последовательностей фазы А имеем:

Вывод 1.

Из условия (48.24) имеем:

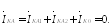
Отсюда

Вывод 2.

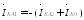
_{Из уравнений (48.19), (48.20), (48.21) выразим напряжения прямой, обратной и нулевой последовательностей:}

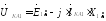
_{Откуда:}

_{Т.к. сумма токов отдельных последовательностей для особой фазы равна нулю, то}

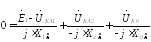
_{На основании 1-го вывода, что}

_{это уравнение преобразуем к виду:}

где

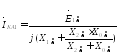
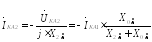
_{Модуль или действующее значение тока прямой последовательности:}

Из самоочевидного условия-

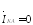
_{Токи поврежденных фаз в месте КЗ}

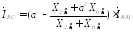
_{Модули комплексных коэффициентов, стоящих перед}в этих выражениях одинаковы; они составляют:

Ток в земле вычисляется по формуле:

или

Векторные диаграммы:

1) Векторная диаграмма напряжений, с учетом вывода 1

_имеем:

2) Векторная диаграмма токов. С учетом (48.24) и вывода 2, т. е.