Лабораторная работа Определение средней длины свободного пробега и эффективного диаметра молекул воздуха

Цель работы: определить длину свободного пробега и эффективный диаметр молекулы азота (молекулы азота составляют 78,1 воздуха).

Методика эксперимента

При тепловом движении молекул происходит их столкновение. Процесс столкновения молекул характеризуют величиной эффективного диаметра молекул – это минимальное расстояние, на которое могут сблизиться центры молекул.

Расстояние, которое проходит молекула между двумя последовательными столкновениями, называется средней длиной свободного пробега молекулы.

Молекулярно-кинетическая теория позволяет получить формулы, связывающие макропараметры газа (давление, объём, температура) с его микропараметрами (размеры молекул, их масса, скорость).

Динамическая вязкость  (коэффициент внутреннего трения) связана со средней длиной свободного пробега молекулы уравнением:

, (2.13) где  плотность газа;  средняя скорость молекул.

Из уравнения (2.13) получим

. (2.14)

Вязкость  можно определить по формуле Пуазейля (2.1):

, (2.15) гдеr – радиус трубки; l – длина трубки; V  объем жидкости, протекшей через сечение трубки за некоторое время t; р  разность давлений на концах трубки.

Средняя скорость молекул газа см. формулу (1.26)

, (2.16) гдеR = 8,31 универсальная газовая постоянная; Т – абсолютная температура;   молярная масса газа.

Плотность газа определяем из уравнения Клапейрона-Менделеева (1.7):

, (2.17) гдер – давление газа.

Подставляя формулы (2.15), (2.16), (2.17) в выражение (2.14), получим:

. (2.18)

Введем коэффициент А, объединив все постоянные величины формулы (2.18): ,

тогда расчетная формула для определения средней длины свободного пробега молекул примет вид:

. (2.19)

Эффективный диаметр d молекулы связан с длиной свободного пробега соотношением

, (2.20) гдеn – концентрация молекул газа при данных условиях

, (2.21)

n₀ = 2,310²⁵м ^-3 – число Лошмидта (концентрация газа при нормальных условиях Т₀ = 273 К, р₀ = 1,0110⁵ Па).

Решая совместно равенства (2.20) и (2.21), получим выражение для эффективного диаметра молекул:

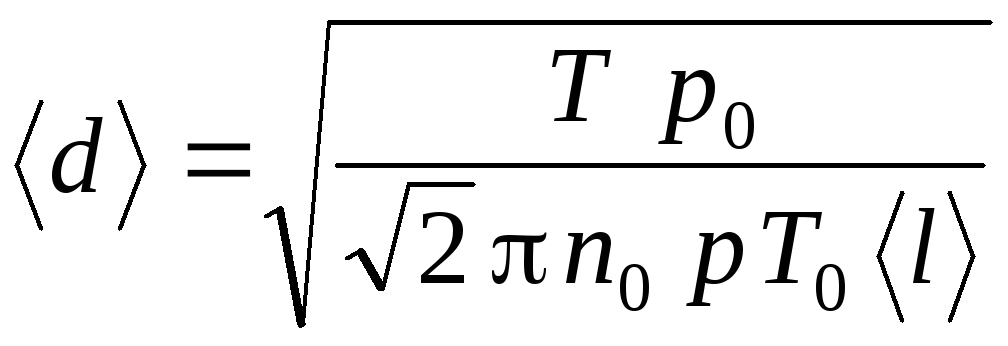. (2.22)

Введем коэффициент b, объединив все постоянные величины формулы (2.22):

.

Р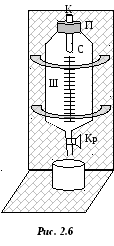асчетная формула для определения эффективного диаметра молекул примет вид:

. (2.23)

Лабораторная работа выполняется на установке, изображенной на рис. 2.6. стеклянный сосуд С с краном Кр закрыт сверху пробкой П, через которую пропущен капилляр К. Для отсчета уровней воды на сосуде имеется шкала Ш. Сосуд С заполняется водой на объема. При открытии крана Кр, вода начинает выливаться из сосуда каплями, а над поверхностью воды создается пониженное давление. Концы капилляра будут находиться под разным давлением: верхний – под атмосферным; нижний – меньше атмосферного. Это обусловливает прохождение воздуха через капилляр.

Порядок выполнения работы

1. Открыв пробку П, заполнить сосуд С водой на 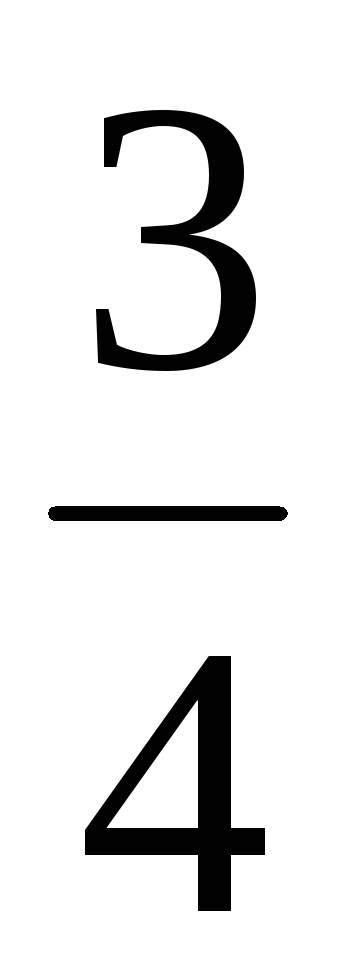объема.

2. Подставить мензурку. Открыв кран Кр, добиться вытекания воды каплями. Включить секундомер.

3. Измерить по шкале высоту h₁ начального уровня воды в момент появления первых капель.

4. Набрав в мензурку объем воды V = 50см³, закрыть кран Кр и остановить секундомер. время t истечения жидкости записать в таблицу 2.4.

5. Измерить уровень h₂ оставшейся в сосуде воды.

6. Определить по термометру температуру воздуха Т в лаборатории, а по барометру  атмосферное давление р.

7. Записать в таблицу значения радиуса r и длины l капилляра, указанные на установке.

8. Пункты 1 – 5 повторить три раза, не изменяя значений h₁ и V.

Таблица 2.4

h1	h2	V	t	Параметры	постоянные	р		D
		50см3		r = l = T = р =	n0 =2,31025м-3 R=8,31 Дж/мольК =2910-3 кг/моль 1 = 103 кг/м3 Т0 = 273 К, Р0 = 1,01105 Па

Обработка результатов измерений

1. вычислить среднее значение времени истекания жидкости .

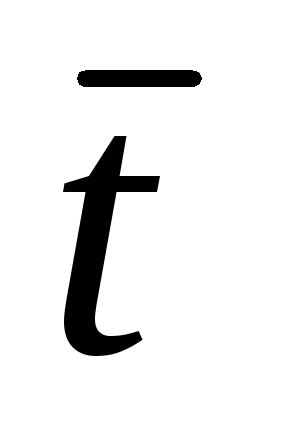2. Вычислить среднее значение высоты .

3. Рассчитать разность давлений р на концах капилляра по формуле

.

4. Вычислить среднюю длину свободного пробега молекулы 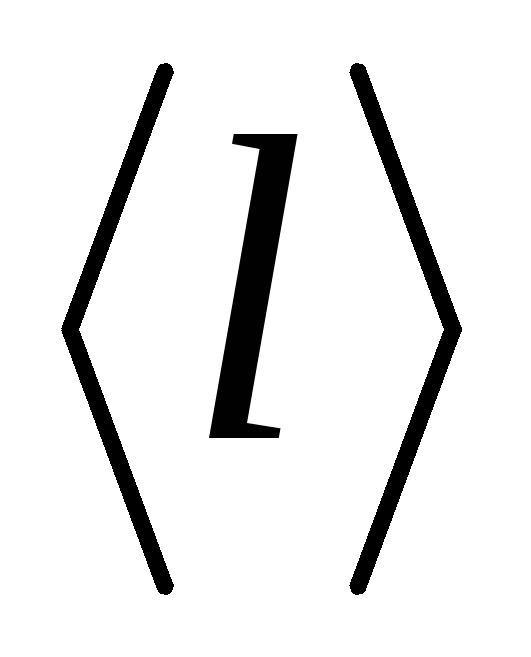по формуле (2.19), подставляя данные таблицы 2.4 в системе СИ (напомним).

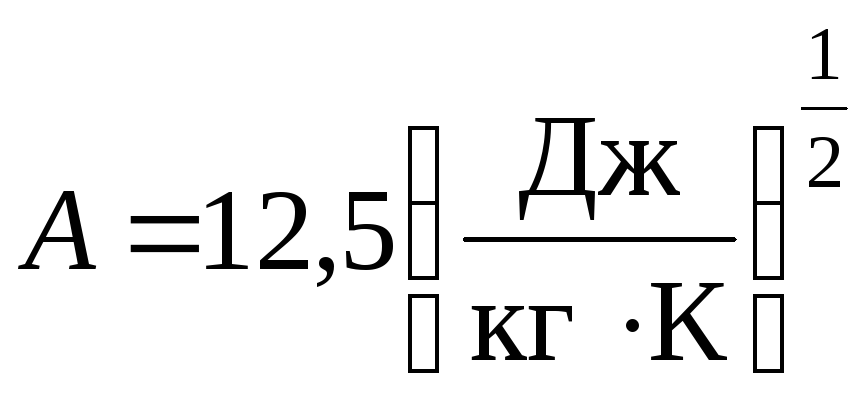5. Рассчитать эффективный диаметр d молекулы воздуха по формуле (2.23), (напомним ).

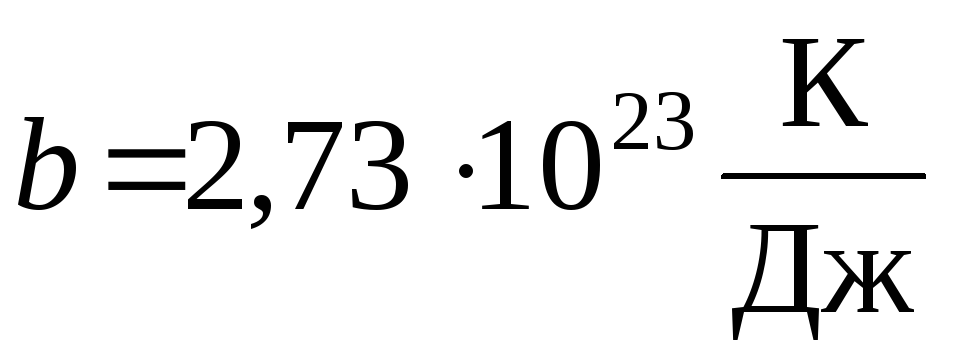6. Сравнить полученные значения средней длины свободного пробега 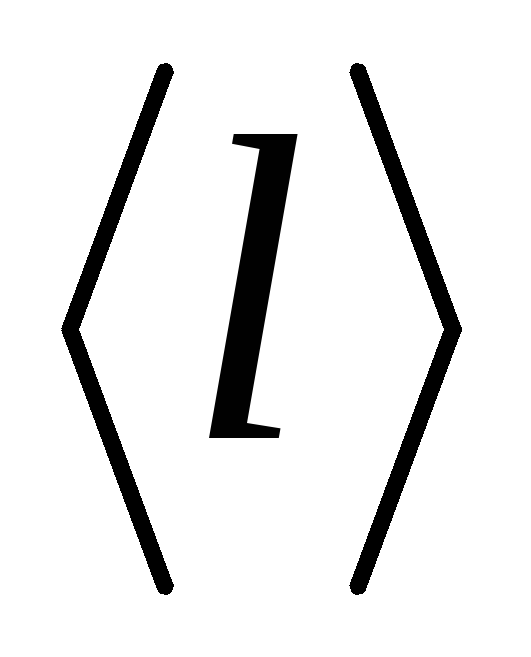и эффективного диаметраd молекулы с табличными (см. приложение).

7. Сделать вывод по проделанной работе.

Контрольные вопросы и задания

1. Что понимают под эффективным диаметром молекулы?

2. Какую величину называют средней длиной свободного пробега?

3. Записать уравнение, связывающее коэффициент внутреннего трения и длину свободного пробега. Выразить из него длину свободного пробега, и объяснить от каких величин она зависит.

4. Какой физический смысл имеет число Лошмидта?

5. Как рассчитывается в данной работе разность давлений на концах капилляра?