
- •Иркутский государственный технический университет молекулярная физика термодинамика
- •Оглавление
- •Введение
- •Молекулярно-кинетическая теория
- •Идеальных газов
- •Исходные понятия и определения
- •Молекулярной физики и термодинамики
- •Молекулярно-кинетическая теория идеальных газов
- •Которое называется распределением Больцмана. Лабораторная работа Определение постоянной Больцмана
- •Лабораторная работа Определение универсальной газовой постоянной
- •2. Явления переноса в термодинамически неравновесных системах
- •Лабораторная работа Определение динамического коэффициента вязкости методом пуазейля
- •Лабораторная работа Определение динамического коэффициента вязкости методом Стокса
- •Лабораторная работа Определение средней длины свободного пробега и эффективного диаметра молекул воздуха
- •Лабораторная работа Определение коэффициента теплопроводности твердых тел
- •3. Термодинамика
- •Взаимосвязь между внутренней энергией, работой и теплотой (первый закон термодинамики)
- •Второе начало термодинамики
- •В незамкнутой системе энтропия всегда возрастает. Функция состояния, дифференциалом которой является , называетсяприведенной теплотой.
- •Основное уравнение термодинамики.Это уравнение объединяет формулы первого и второго начала термодинамики:
- •Подставим уравнение (3.9), выражающее второе начало термодинамики, в равенство (3.10):
- •Лабораторная работа Определение отношения теплоемкостей газов методом клемана - дезорма
- •Лабораторная работа Определение изменения энтропии при изохорическом процессе в газе
- •Лабораторная работа Определение адиабатической постоянной по скорости звука в воздухе
- •4. Свойства жидкостей
- •Лабораторная работа Определение коэффициента поверхностного натяжения жидкости
- •Заключение
Лабораторная работа Определение динамического коэффициента вязкости методом пуазейля
Цель работы: определить динамический коэффициент вязкости жидкости методом Пуазейля.
Методика эксперимента
Существуют два вида течения жидкости: ламинарное и турбулентное. Для ламинарного течения характерно сохранение слоев жидкости, они скользят относительно друг друга, не перемешиваясь. Для турбулентного течения характерно быстрое перемешивание слоев жидкости.
Рассмотрим ламинарное течение жидкости (рис. 2.2) вдоль трубы длиной l и радиусом R под действием перепада давлений р = р1 р2.
Выделим мысленно внутри жидкости цилиндрическую поверхность радиуса r, коаксиальную трубе. Если S – площадь этой поверхности, то сила внутреннего трения
![]() . (2.2)
. (2.2)
В стационарных условиях сила внутреннего
трения уравновешивается разностью сил
давления на концах цилиндра
стационарных условиях сила внутреннего
трения уравновешивается разностью сил
давления на концах цилиндра
![]() . (2.3)
. (2.3)
Приравнивая выражения (2.2) и (2.3), находим:
![]() .
.
Интегрируя последнюю формулу, получаем выражение для средней скорости текущей жидкости:
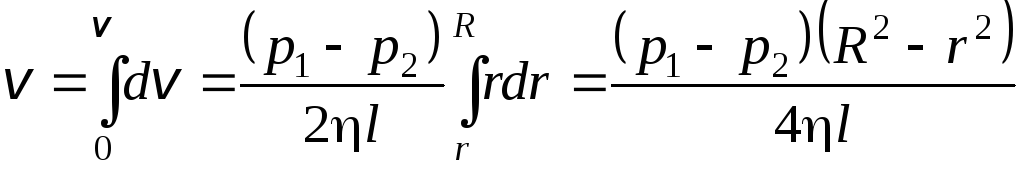 . (2.4)
. (2.4)
Найдем объем V жидкости, вытекающий из трубы за единицу времени. Из цилиндрического слоя радиусом r и толщиной dr вытекает объем жидкости
![]() . (2.5)
. (2.5)
Подставив выражение (2.4) в формулу (2.5) и проинтегрировав по r в пределах от 0 до R, находим объем жидкости, вытекающий в единицу времени из трубы радиусом R и длиной l при перепаде давлений на ее концах (р1 р2), получим формулу Пуазейля (2.1):
![]() .
.
В течение времени t из трубы вытечет объем жидкости
![]() ,
отсюда
динамический коэффициент вязкости
,
отсюда
динамический коэффициент вязкости
![]() . (2.6)
. (2.6)
Схема установки приведена на рис. 2.3. В нижней части боковой стенки сосуда С, стоящего на подставке П, сделано отверстие, из которого может вытекать жидкость, налитая в сосуд, по трубе Т в мензурку М. Чтобы использовать формулу Пуазейля, нужно найти перепад давлений вдоль трубки Т: (р1–р2). Давление на верхнем конце трубки определяется средней высотой уровня жидкости относительно высоты нижнего конца трубки

![]() ,
гдеh1
и h2
уровни жидкости в сосуде С относительно
поверхности стола соответственно в
начале и в конце эксперимента; h
– высота свободного конца трубки над
поверхностью стола.
,
гдеh1
и h2
уровни жидкости в сосуде С относительно
поверхности стола соответственно в
начале и в конце эксперимента; h
– высота свободного конца трубки над
поверхностью стола.
Таким образом
![]() ,
где
плотность жидкости; g
= 9,8 м/с2
– ускорение свободного падения.
,
где
плотность жидкости; g
= 9,8 м/с2
– ускорение свободного падения.
Давление на нижнем
конце трубки равно атмосферному, но,
поскольку атмосферное давление действует
и на жидкость в сосуде, можно положить
![]() ,
следовательно:
,
следовательно:
![]() .
.
Подставив последнее выражение в равенство (2.6), получим расчетную формулу:
 , (2.7)
гдеt
время истечения из трубки жидкости
объемом V;
l
– длина трубки; d
= 2r
– внутренний диаметр трубки.
, (2.7)
гдеt
время истечения из трубки жидкости
объемом V;
l
– длина трубки; d
= 2r
– внутренний диаметр трубки.
Порядок выполнения работы
Измерить внутренний диаметр d трубки измерительным микроскопом.
Измерить длину l трубки линейкой.
Налить воду в сосуд С. Измерить высоту начального уровня воды h1.
Наклонив трубку Т, включить секундомер и измерить время t вытекания воды в мерный стакан.
Измерить высоту h свободного конца трубки Т над поверхностью стола.
Измерить объем V вылившейся жидкости.
Измерить высоту h2 конечного уровня воды в сосуде С.
Пункты (3 - 7) повторить три раза, не изменяя значений h1 и h.
Данные измерений занести в таблицу 2.2.
Таблица 2.2
|
h1,м |
h,м |
h2,м |
|
V,м3 |
|
t, с |
|
Параметры |
|
|
|
|
|
|
|
|
|
|
|
|
d = l = = |
|
|
|
|
|
|
| |||||||||
|
|
|
|
Обработка результатов измерений
Рассчитать средние значения величин
 ,
, ,
, .
.По формуле (2.7) рассчитать динамический коэффициент вязкости , подставляя средние значения
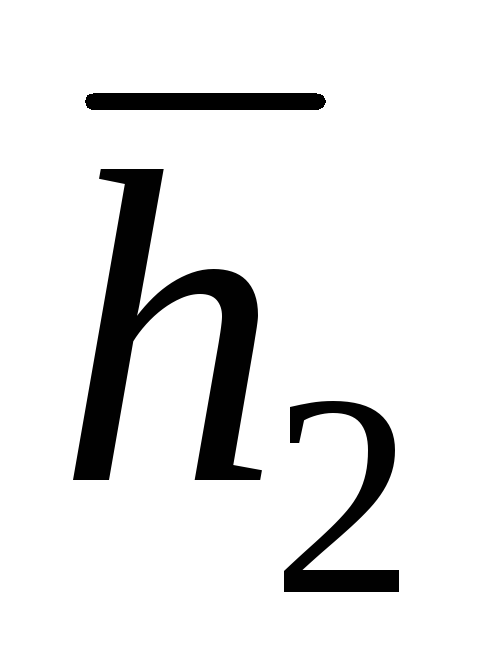 ,
, ,
, и данные таблицы 2.2 в системе СИ.
и данные таблицы 2.2 в системе СИ.Рассчитать относительную погрешность определения динамического коэффициента вязкости по формуле
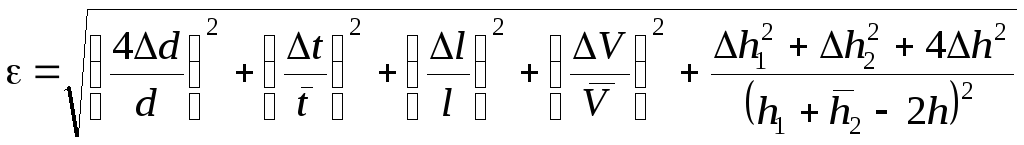 .
.
Рассчитать абсолютную погрешность определения динамического коэффициента вязкости по формуле

Записать результат работы в виде
 ед. изм.
ед. изм.Сравнить полученный коэффициент вязкости воды с табличным. Сделать вывод по проделанной работе.
Контрольные вопросы и задания
Что называется равновесным состоянием, релаксацией, явлением переноса?
Дайте понятие градиента.
Запишите уравнение переноса.
Объясните механизм возникновения внутреннего трения.
Дайте определение динамического коэффициента вязкости.
Назовите виды течения жидкостей.
