Которое называется распределением Больцмана. Лабораторная работа Определение постоянной Больцмана

Цель работы: 1 экспериментально подтвердить зависимость давления газа от концентрации молекул при постоянной температуре газа; 2  определить постоянную Больцмана.

Методика эксперимента

Давление газа пропорционально концентрации молекул n и термодинамической температуре Т газа см. формулу (1.8):

,

где k  постоянная Больцмана.

Если изменить концентрацию молекул на величину n при неизменной температуре газа, то давление газа изменится на величину p:

.

Изменение давления газа при постоянной температуре пропорционально изменению концентрации молекул газа.

Целью работы является экспериментальное подтверждение зависимости (1.34) при Т = const и определение постоянной Больцмана.

Используемая в лабораторной работе установка (рис. 1.8) состоит из сосуда С, объем которого V_C известен; шприца Ш; U-образного водяного манометра М и крана К. Резиновый шланг 1 соединяет сосуд с одним из колен манометра, шланг 2 соединяет шприц (через кран) с сосудом.

Р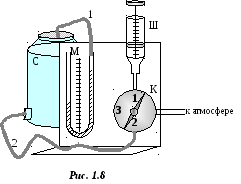укоятка крана имеет три положения: в положении "1 полости сосуда и шприца сообщаются друг с другом и с атмосферой; в положении 2 связь сосуда и шприца с атмосферой прекращается; в положении 3 происходит полная изоляция сосуда и восстанавливается связь шприца с атмосферой.

В начальный момент времени рукоятку крана ставят в положении 1, в шприц из атмосферы набирают определенный объем V_Ш воздуха. При этом температура Т воздуха в сосуде и шприце равна температуре воздуха в аудитории. Давления воздуха в шприце и в сосуде будут равны атмосферному р = р_А. Разность уровней жидкости в коленах манометра равна нулю. Число молекул N, находящихся в объеме V_Ш шприца:

, (1.17) где  число молей воздуха; N_А – число Авогадро; V_ш,0 – объем, который занимал бы воздух в шприце при нормальных условиях; V_,0 = 22,4 л – объем одного моля газа при нормальных условиях (см. приложение).

Определим, каким был бы объем воздуха в шприце при нормальных условиях. Для этого запишем уравнение состояния газа см. формулу (1.6):

, отсюда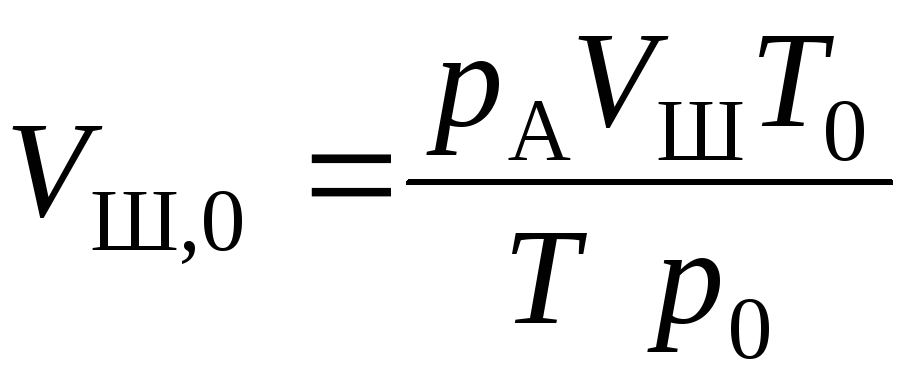, гдер₀ = 1,0110⁵ Па; Т₀ = 273К – давление и температура газа при нормальных условиях.

Подставив последнее выражение в уравнение (1.17), получим:

. (1.18)

Повернув рукоятку крана в положение 2 и, переводя газ из шприца в сосуд, увеличиваем концентрацию газа в сосуде на величину n:

. (1.19)

Подставив формулу (1.18) в выражение (1.19), получим:

, (1.20) гдер_А  атмосферное давление; р₀ = 760 мм Hg = 1,0110⁵ Па; Т₀ = 273К; N_А = 6,0210²³ моль^-1; Т  температура воздуха в аудитории; V_,0 = 22,410^-3 м³; V_С – объем сосуда; V_Ш – объем воздуха, набираемого шприцем.

Обозначим , (1.21)

тогда формула (1.20) будет иметь вид . (1.22)

Изменение концентрации молекул в сосуде вызовет изменение давления (р = n k T) на величину р. В связи с этим высота столбика жидкости в колене манометра, соединенном с сосудом, уменьшится, а в другом – увеличится. Разность давлений найдем по формуле:

, (1.23) где разность уровней жидкости в коленах манометра;  = 10³ кг/м³ – плотность воды; g = 9,81 м/с² – ускорение свободного падения тел.

в формуле (1.23) обозначим B = g, (1.24)

тогда : р = Вh. (1.25)

Порядок выполнения работы

1. Поставить кран К в положение 1. Набрать в шприц воздух объемом V_ш = 10 см³. Перевести кран в положение 2.

2. Ввести воздух из шприца в сосуд. Рукоятку крана перевести в положение 3, повернув ее по часовой стрелке на 90.

3. Подождать 1 – 1,5 минуты, пока прекратится перемещение жидкости в коленах манометра. Измерить по шкале манометра М высоты уровней жидкости h₁ и h₂. Результаты измерений занести в таблицу 1.1.

4. Оставить кран в положении 3. Набрать в шприц воздух объемом V_ш = 10 см³. Перевести кран в положение 2. Ввести воздух из шприца в сосуд. Вернуть кран в положение 3. Таким образом, в сосуд уже будет введено 20 см³ воздуха.

5. Подождать 1 – 1,5 минуты, пока прекратится перемещение жидкости в коленах манометра. Измерить по шкале манометра М высоты уровней жидкости h₁ и h₂. Результаты измерений занести в таблицу 1.1.

6. Повторить пункты 4, 5 два раза. При этом в сосуд уже будет введено соответственно 30 см³, затем 40 см³ воздуха.

7. По шкале барометра определите величину атмосферного давления р.

8. По шкале термометра определите температуру воздуха в аудитории Т.

Таблица 1.1

VШ,м3	h1, мм	h2, мм	h, м	рА, мм Hg	Т, К	VC, м3	А, м-6	В кг/м2с2	n, м-3	р, Па	k, Дж/К
1010-6						2,3510-3
2010-6
3010-6
4010-6

Обработка результатов измерений

1. Вычислить постоянные А и В по формулам (1.21) и (1.24).

2. Используя формулы (1.22) и (1.25), вычислить для каждого из четырех измерений величины n и р. Результаты вычислений записать в таблицу 1.1.

3. Построить график зависимостир = f(n). Прямую, проходящую через ноль, проводим усредненно.

4. Определить по графику

.

5. Вычислить постоянную Больцмана .

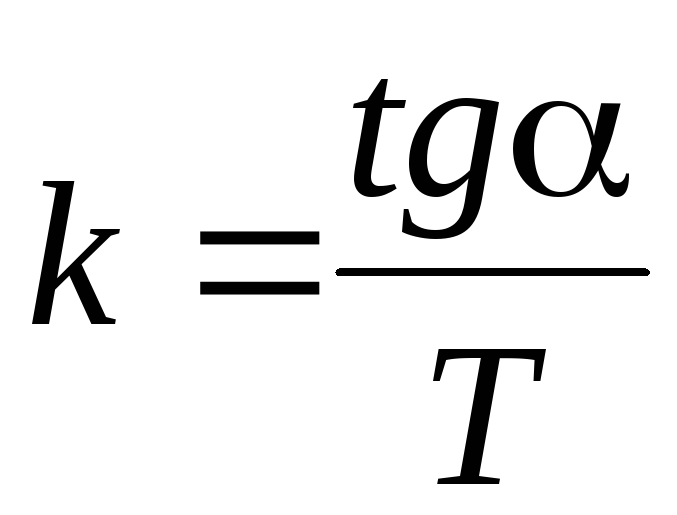6. Сравнить полученное значение постоянной Больцмана с табличным.

7. Сделать вывод по проделанной работе.

Контрольные вопросы и задания

1. Запишите уравнение Клайперона-Менделеева для произвольной массы газа и для одного моля.

2. Чему равно численное значение универсальной газовой постоянной?

3. Запишите уравнение молекулярно-кинетической теории идеального газа.

4. Запишите формулу, выражающую связь между термодинамической температурой газа и средней кинетической энергией теплового движения молекул.

5. Запишите формулу, выражающую связь постоянной Больцмана с универсальной газовой постоянной и числом Авогадро.

6. Какой физический смысл имеет постоянная Больцмана?

7. Как давление газа, находящегося при постоянной температуре, зависит от концентрации молекул?