
Литература от Абакумова ч2 / Осмотический массоперенос
.pdf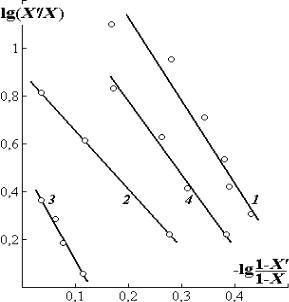
|
Из экспериментальных графи- |
||
|
ков (рис. 1.25) находятся константы |
||
|
K и величины среднего заряда ZB* . |
||
|
Последние определяются по угло- |
||
|
вым коэффициентам ZB* / Z A* |
линей- |
|
|
ных графиков. Значения Z A* |
в расче- |
|
|
тах принимались равными единице, |
||
|
так как в гуминовых кислотах и ка- |
||
|
тионитах происходит обмен водоро- |
||
|
да на ионы металлов. |
|
|
|
Результаты расчетов парамет- |
||
|
ров ионного обмена для двухвалент- |
||
|
ных ионов кальция и бария приведе- |
||
Рис. 1.25. Изотермы ионного обмена ио- |
ны в табл. 1.4. В ней также даны рас- |
||
нов Н+ катионитов КУ-1 (1); КРС-10т (2); |
четные значения долей ионных ассо- |
||
КБ-4 (3) и гуминовой кислоты (4) на ио- |
циатов и ионов, которые взаимодей- |
||
ны Ca2+ гидроксида кальция Ca(OH)2 |
ствуют |
с диссоциированными ИГ |
|
|
одной или двумя валентностями. |
||
Согласно экспериментам значения ZB* |
во всех опытах меньше двух |
||
[19]. Константы ионного обмена K изменяются в пределах одного порядка в зависимости от концентрации и состава соединений, в которые входят катионы.
Обмен ионов водорода на ионы кальция и бария с различной степенью вероятности происходит по приведенным ниже схемам:
1. а) R - COOH + MeCl2 + H2O → R - COOMeOH + 2HCl ,
R - COOH + МеCl2 |
→ R - COOМеO - R′+ 2HCl |
b) ′ |
, |
R -OH |
|
с) 2R - COOH + МеCl2 → R - COOМеOОО- R + 2HCl ;
2.a) R′- OH + MeCl2 + H2O → R′- OМеOH + 2HCl , b) 2R′- OH + MeCl2 → R′- OМеO - R′+2HCl ,
где Ме — двухвалентный катион, R и R' — соответственно звенья макромолекул, содержащие карбоксильные и гидроксильные группы.
В каждом конкретном случае превалируют две, три приведенные реакции. Так, если значения Z* больше единицы (табл. 1.4), то ионный обмен протекает преимущественно по схемам 1а и 2а. При значениях Z*, близких к двум, — по схемам 1b, 1с и 2b.
Для замещения ионов водорода на ионы металлов в момент образования ионных связей предварительно должны произойти диссоциации
41

групп СООН→СОО– + Н+, молекул воды Н2О→Н+ + ОН– и соли
MeCl2 →Me2+ + 2Cl–.
Сразу после диссоциации вокруг ионов образуются гидратные оболочки. Они препятствуют непосредственным контактам взаимодействующей паре катион-анион. Следует также учитывать малую интенсивность диффузии гидратированных ионов внутри микропористой структуры матрицы ионита. Все это, в целом, существенно снижает вероятность образования ионных связей по схеме 1а.
Таблица 1.4. Значения параметров обмена катионов кальция и бария на гуминовых кислотах и синтетических ионитах
|
|
Концентрация |
Значения |
Доля катионов |
|||
Катионит |
Соединение |
с валентностью |
|||||
катиона, мэкв/л |
|
|
|||||
K |
* |
1 |
2 |
||||
|
|
|
Z |
||||
ГК 1 |
Ca(OH)2 |
0,02–0,2 |
2,87 |
1,45 |
0,55 |
0,45 |
|
Ca(CH3COO)2 |
1,74 |
1,6 |
0,4 |
0,6 |
|||
|
|
||||||
ГК 2 |
BaCl2 |
0,1–0,3 |
2,99 |
1 |
1 |
0 |
|
ГК 3 |
BaCl2 |
0,1–0,4 |
1,64 |
1,7 |
0,3 |
0,7 |
|
|
Ca(OH)2 |
|
3,31 |
1,76 |
0,24 |
0,76 |
|
КУ-1 |
CaCl2 |
0,02–0,2 |
2,81 |
1,26 |
0,74 |
0,26 |
|
Ca(CH3COO)2 |
2,32 |
1,5 |
0,85 |
0,15 |
|||
|
|
||||||
|
Ba(OH)2 |
|
6,02 |
1 |
1 |
0 |
|
КРС-10т |
Ca(CH3COO)2 |
0,02–0,2 |
2,82 |
1,35 |
0,65 |
0,35 |
|
Ca(OH)2 |
2,35 |
1,21 |
0,79 |
0,21 |
|||
|
Ba(OH)2 |
|
3,09 |
1,11 |
0,89 |
0,11 |
|
Молселект |
BaCl2 |
0,1–0,6 |
6,92 |
1,27 |
0,73 |
0,23 |
|
BaCl2 |
0,01–0,07 |
10,23 |
1 |
1 |
0 |
||
|
|||||||
КБ-4 |
Ca(CH3COO)2 |
0,02–0,2 |
1,4 |
1,82 |
0,18 |
0,82 |
|
Ba(OH)2 |
1,37 |
1,65 |
0,35 |
0,65 |
|||
|
|
||||||
Еще меньшая вероятность образования двойных ионных связей с функциональными ионогенными группами контактирующих звеньев макромолекул (схема 1с). Для этого необходимо, чтобы они были в непосредственном контакте и диссоциировали одновременно.
Время «жизни» двойных ионных связей существенно больше, чем одинарных. При наличии у катиона нескольких ионных связей снижается подвижность макромолекул и происходит уплотнение матрицы ионита. Подобные процессы имеют место при ионном обмене по другим схемам
(1b, 2a, 2b).
Если во внешнем растворе находятся сульфат или ацетат меди (табл. 1.5), то вследствие обмена ионов меди на ионы водорода функциональных групп гуминовых кислот (ГК) образуются серная или уксусная кислоты. Гуминовые кислоты ГК 2, ГК 3 имели разный состав, так как были получены из различных видов торфа.
В процессе опыта наблюдается интенсивное уплотнение (коагуляция) ассоциатов ГК. Их проницаемость уменьшается.
42
Если ионы Н+ и поливалентных металлов заменяются одновалентными (например, калия, натрия), то происходит уменьшение числа водородных и ионных связей между макромолекулами. Это вызывает пептизацию — разукрупнение ассоциатов макромолекул.
Таблица 1.5. Значения параметра обмена ионов меди на гуминовых кислотах
|
|
Концентрация |
|
* |
Доля катионов с валентностью |
|
Ионит |
Соединение |
катиона, мэкв/л |
К |
Z |
|
|
1 |
2 |
|||||
ГК3 |
Cu(CH3COO)2 |
0,1–0,24 |
2 |
1,95 |
0,05 |
0,95 |
ГК3 |
Cu(CH3COO)2 |
0,2–2 |
3,22 |
1,87 |
0,13 |
0,87 |
ГК2 |
Cu(CH3COO)2 |
0,1–0,24 |
3,45 |
1,95 |
0,05 |
0,95 |
ГК2 |
Cu(CH3COO)2 |
0,2–2 |
6,31 |
2 |
– |
1 |
ГК3 |
CuSO4 |
0,5–2 |
2,45 |
1,45 |
0,55 |
0,45 |
ГК2 |
CuSO4 |
0,5–2 |
2,67 |
1,65 |
0,35 |
0,65 |
ГК3 |
CuSO4 |
0,07–0,25 |
4,75 |
1,4 |
0,6 |
0,4 |
ГК2 |
CuSO4 |
0,07–0,25 |
4,78 |
1,54 |
0,46 |
0,54 |
Малые по размеру анионы SO42– могут проникать в микропоры частиц ГК. Между ними и поливалентными катионами возникает электростатическое притяжение. Это снижает средний заряд их взаимодействия со связанными анионами — диссоциированными ИГ (Z* < 2).
Для анионов (CH3COO)–1 вероятность диффузии их в микропоры уплотненной матрицы ГК меньше, чем анионов SO42–. Поэтому экспериментальные значения среднего заряда Z* стремятся к двум.
Взаимодействия ионов железа и их ассоциатов с катионитами (например, КУ-1) разнообразны. Приведем несколько схем.
1.а) R-SO3H +Fe(OH)2Cl →(R-SO3)-[Fe(OH)2] +HCl,
b)2(R-SO3H) +Fe(OH)Cl2 →2(R-SO3)-[Fe(OH)] +2HCl, с) 3(R-SO3H) +Fe(OH)Cl2 →3(R-SO3)-Fe +2HCl + H2O.
2.а) 2(R-SO3H) +FeSO4 →2(R-SO3)-Fe +H2SO4,
b)R-SO3H +FeSO4 +H2O →(R-SO3)-[Fe(OH)] +H2SO4.
Гидроксилы, входящие в соединения железа (правые части реакций 1а, 1b, 2b), могут замещаться другими свободными анионами. Вероятность взаимодействия катиона Fe3+ с тремя одновременно диссоциированными и контактирующими ионогенными группами очень мала (схема 1с). В этом случае возможно вначале поглощение ионитом ассоциатов железа по схеме 1а. Далее происходит отделение от ассоциата группы ОН– и взаимодействие с другим связанным анионом. Затем имеет место последующее удаление гидроксила и взаимодействие с третьей диссоциированной ионогенной группой. Такой механизм возможен, если в процессе поворотов звеньев макромолекул их диссоциированные функциональные группы будут находиться на расстояниях ионной связи. Если этого не достигается, то
43
ион железа и ассоциаты Fe3+ имеют электростатическое взаимодействие с ближайшими связанными анионами.
Для двух- и трехвалентных ионов железа значения Z* не достигают их валентностей (табл. 1.6). Для различных по составу, размерам, времени «жизни» ионных ассоциатов и энергии взаимодействия их со связанными анионами значения Z* могут быть в пределах от нуля до Z.
С увеличением концентрации солей железа (схема 1 с) вероятность образования гидроксидов Fe(OH)3 уменьшается. В связи с этим снижаются значения pH из-за увеличения количества ионов водорода, которые вытесняются ионами Fe3+ из внутреннего во внешний раствор.
Ионы железа приводят к уплотнению матрицы. Образуются ионные связи между ИГ соседних макромолекул. По этой причине уменьшается вероятность образования и поступление ионных ассоциатов железа [Fe(OH)]2+, [Fe(OH)2]1+ во внутриматричный раствор.
Таблица 1.6. Значение параметров обмена ионов железа на гуминовых кислотах и синтетических ионитах
|
|
|
|
|
|
|
|
|
|
Соеди- |
Концентрация |
|
* |
Доля катионов с валентностью* |
|||
Ионит |
нение |
катиона, мэкв/л |
K |
Z |
|
|
|
|
0 |
1 |
2 |
3 |
|||||
ГК2 |
FeSO4 |
0,005–0,7 |
2,48 |
0,79 |
0,21 |
0,79 |
- |
- |
ГК3 |
FeSO4 |
0,005–0,7 |
2,47 |
0,55 |
0,45 |
0,55 |
- |
- |
ГК3 |
FeCl3 |
0,005–0,1 |
2,44 |
0,98 |
0,02 |
0,98 |
- |
- |
ГК2 |
FeCl3 |
0,2–0,7 |
2,11 |
2,48 |
- |
- |
0,52 |
0,48 |
ГК3 |
FeCl3 |
0,005–0,05 |
2,59 |
0,82 |
0,18 |
0,82 |
- |
- |
КУ-1 |
FeCl3 |
0,02–0,2 |
2,34 |
1,11 |
- |
0,89 |
0,11 |
- |
КУ-1 |
FeSO4 |
0,005–0,2 |
2,38 |
1,39 |
- |
0,61 |
0,39 |
- |
КБ-4 |
FeCl3 |
0,02–0,2 |
1,29 |
1,45 |
- |
0,55 |
0,45 |
- |
КБ-4 |
FeSO4 |
0,005–0,7 |
1,78 |
0,6 |
0,4 |
0,6 |
- |
- |
КБ-4 |
FeCl3 |
0,005–0,7 |
2,92 |
2,25 |
- |
- |
0,75 |
0,25 |
КБ-4 |
FeCl3 |
0,03–0,8 |
3,63 |
1,16 |
- |
0,84 |
0,16 |
- |
Молселект |
FeCl3 |
0,005–0,5 |
1,35 |
1,15 |
- |
0,85 |
0,15 |
- |
* Значению 0 соответствует физическая сорбция молекул или их ассоциатов (микрокристаллов) на ионите
Из приведенных результатов следует, что получаемая в опытах обменная емкость в большинстве случаев не равна содержанию ИГ в ионитах. Она лишь отражает установившееся динамическое равновесие между каждым конкретным раствором электролита и катионитом. Это равновесие зависит от физико-химических свойств ионита, раствора и внешних термодинамических характеристик среды. Поэтому хемосорбционным методом (например, применяя ион бария) можно только приближенно оценить количество ионогенных групп в ионите.
Экспериментальные результаты и модели кинетики и динамики ионного обмена приведены в работах [19–20].
44
2. ИСПАРЕНИЕ ИЗ КАПИЛЛЯРОВ
Тепломассоперенос в реальных дисперсных системах представляет совокупность основных и сопутствующих потоков тепла и вещества, которые сопровождаются фазовыми переходами, химическими превращениями и изменением структуры этих тел. Поэтому процессы переноса следует вначале рассматривать в простейших модельных телах, а затем перейти к рассмотрению этих процессов в более сложных реальных материалах. В модельных телах представляется возможным исключить сопутствующие явления, которые имеют место в реальных телах. Однако полученные закономерности в модельных средах, в свою очередь, нельзя полностью переносить на процессы массопереноса в сложных дисперсных и пористых материалах. В этом случае необходимо учитывать все основные и сопутствующие переносу тепла и вещества факторы.
Простейшей моделью является система капилляров. Изучение испарения в отдельных капиллярах дает возможность судить о подобных процессах в пористых материалах, имеющих жесткую постоянную структуру.
2.1.Компьютерное моделирование испарения жидкости из капилляров
С целью определения потока вылетевших молекул из плоского капилляра, установления в нем мениска и адсорбированных пленок влаги был проведен расчет методом Монте-Карло. Преимуществом вычислительного эксперимента по сравнению с реальным физическим опытом является возможность проследить траекторию каждой частицы и определить потоки частиц после любого i-го столкновения частиц со стенками [21, 22]. В каждом вычислительном эксперименте моделировалось испарение частиц с массами, равными 18 атомным единицам массы, при неизменной температуре среды 300 К. Взаимодействие частиц со стенками капилляров принималось полностью диффузионным.
При проведении расчетов предполагалось, что молекула не имеет энергию, необходимую для преодоления связи со стенкой капилляра. В этом случае она адсорбируется на стенке в течение всего времени испарения N частиц. Если процесс испарения отклонялся от установившегося, то
45
число адсорбируемых молекул на стенке уменьшалось или возрастало по мере роста или снижения интенсивности испарения.
Капилляр заданной высоты разделялся на двадцать равных зон n и рассчитывалось число частиц попавших в каждую зону. В каждом вычислительном эксперименте для определенных значений относительной вели-
|
чины капилляра Н= L/R (L — длина и R |
|
|
— радиус (половина ширины) капилля- |
|
|
ра), энергии связи и температуры «уча- |
|
|
ствовало» 105 частиц. |
|
|
Сначала рассчитывали перемеще- |
|
|
ния внутри зазора и взаимодействие со |
|
|
стенками щели первой частицы. В ре- |
|
|
зультате перемещения частица могла |
|
|
вылететь из капилляра, адсорбироваться |
|
|
на стенке или вернуться обратно в жид- |
|
|
кость. Затем проводились подобные вы- |
|
|
числения для последующих частиц. |
|
|
Компьютерное моделирование по- |
|
|
казало, что для плоских капилляров с |
|
|
относительными размерами Н≤1 веро- |
|
|
ятность вылета молекул из них мало за- |
|
|
висит от числа столкновений молекул с |
|
|
его стенками. Для капилляров, имеющих |
|
|
Н>>1, возрастает число адсорбирован- |
|
|
ных молекул на стенках, что существен- |
|
|
но снижает вероятность вылета частиц |
|
|
из капилляров. Для всех значений Н ко- |
|
|
личество возвращающихся |
обратно в |
|
жидкую фазу молекул больше, чем их |
|
|
выход из капилляров. |
|
|
Согласно расчетам на внутренней |
|
|
поверхности капилляров |
образуется |
|
уменьшающийся от мениска к устью по |
|
|
толщине слой адсорбированного веще- |
|
|
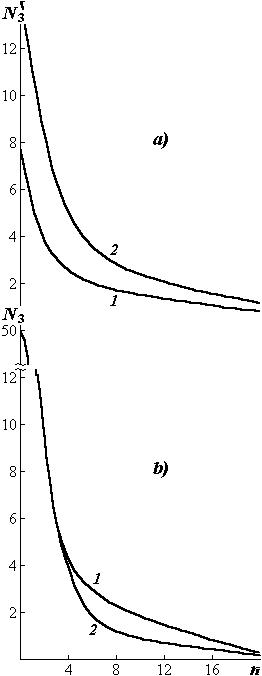
ства (рис. 2.1). Наличие адсорбирован- |
|
|
ной пленки не приводит к существенно- |
|
|
му увеличению числа вылетевших мо- |
|
Рис. 2.1. Распределение адсорбиро- |
лекул из капилляра в вакуум. Макси- |
|
ванных на стенке капилляра частиц с |
мально возможное превышение — не |
|
энергией связи 4,2 (1) и 42 (2) |
более 3%. |
|
кДж/моль при Т=300 К в зонах n ка- |
При испарении молекул в парога- |
|
пилляров с относительной высотой |
зовую среду возникает миграция моле- |
|
Н=1 (а) и 10 (b) |
кул окружающего капилляр газа (для |
|
|
46 |
|

воздуха — кислорода, азота и других молекул) к мениску. Молекулы испаряющегося вещества сталкиваются с ними. Интенсивность столкновения молекул в паровой фазе зависит от концентрации молекул внешнего газа. Это приводит к снижению числа молекул пара, которые покидают капилляр. Увеличивается количество молекул, которые возвращаются обратно в жидкость и адсорбируются на стенках капилляра.
Количество адсорбированных молекул возрастает с увеличением их концентрации в капилляре и энергии связи со стенкой. Особенно существенным увеличение толщины пленки вблизи мениска.
2.2.Испарение из капилляров при температурах ниже точки кипения жидкостей
Наблюдения за испарением воды из стеклянных и кварцевых цилиндрических капилляров различных диаметров в вакуум или атмосферу при температуре Т<373 К проводили в специальной камере, из которой предварительно откачивали воздух до давления 13 Па. В камеру помещали капилляры. Один конец капилляров был запаян, другой открыт. Капилляры заполняли дистиллированной водой. С открытого конца (устья) капилляра происходило испарение жидкости. В зависимости от расстояния между устьем и мениском капилляра l фиксировали обратную величину скорости испарения v в вакуум [23].
При ϕ<0,6 графики зависимости v–1 =f(l) для всех диаметров капилляров d =1–100 мкм линейные. Они исходят из начала координат. В этом случае пленки влаги на стенках капилляров отсутствуют. При ϕ>0,6 зависимости v–1 =f(l) имеют два участка (рис. 2.2, графики 1–4). Для капилляров с размерами d >40 мкм наблюдается один прямолинейный участок (график 5). Путем экстраполяции второго прямолинейного участка графиков до оси абсцисс можно определить длину пленки влаги на стенке капилляра l*.
Относительная влажность от мениска до устья капилляра изменяется от единицы у мениска до φ — относительной влажности внешней парогазовой среды. В каждом сече-
47

нии капилляра пленка находится в динамическом равновесии с контактирующим с ним паром. Концентрация пара пропорциональна его парциальному давлению p. С увеличением φ длина пленки возрастает. Поэтому пленочное течение в капиллярах существенно при высоких значениях φ внешней парогазовой среды. Наличие пленок влаги способствует увеличению интенсивности массопереноса за счет миграции конденсированной
влаги в самой пленке по направлению потока пара. |
|
||||
|
|
|
Согласно экспериментам (рис. 2.3) |
||
|
|
|
|||
|
|
|
длина пленки l* в диапазоне внутренних |
||
|
|
|
диаметров капилляров от 30 до 2 мкм ли- |
||
|
|
|
нейно возрастает. В капиллярах диаметром |
||
|
|
|
d > 30 мкм пленки не наблюдались. |
||
|
|
|
Опыты |
при ϕ≥0,5 |
с капиллярами, |
|
|
|
имеющими внутренние размеры от 1 до 150 |
||
|
|
|
мкм, показали, что толщина их стенок |
||
|
|
|
|||
|
|
|
практически не влияет на снижение темпе- |
||
Рис. 2.3. Зависимость длины во- |
ратуры в зоне испарения. Максимальное |
||||
допроводящей пленки l* (мм) от |
понижение |
температуры |
испаряющейся |
||
диаметра капилляров d (мкм) при |
жидкости у мениска не превышало 0,1 К. |
||||
условиях: ϕ=0,96, Т=314 К (1); |
При испарении в вакуум (ϕ→0) со скоро- |
||||
0,86 и 304 К (2); 0,95 и 293 К (3); |
|||||
0,96 и 304 К (4) |
стью 4,4 10–5 |
м/с понижение температуры |
|||
достигает 1,6 К. При малых скоростях испарения (v <3 10–6 м/с) изменением температуры вблизи мениска можно пренебречь. В этом случае обеспечивается достаточный подвод тепла через стенки стеклянных капилляров в пределах 20–200 мкм в зону испарения.
Механизм массопереноса в парогазовую среду при обычном барометрическом давлении осложняется притоком молекул газа (кислорода, азота) во внутрь капилляра. Это снижает вынос молекул воды из капилляров и способствует образованию толстых пленок вблизи менисков при высоких значениях ϕ.
При отсутствии пленок влаги скорость испарения v =dl/dτ рассчитывается по формуле Стефана
v = |
DPV |
|
|
ln |
P − p0 |
, |
(2.2.1) |
В |
|||||||
|
|
|
|||||
|
RTl |
P − pl |
|
||||
где VВ — молярный объем воды; l — расстояние от устья капилляра до
мениска; р0 и рl — соответственно парциальное давление водяного пара во внешней среде и над поверхностью мениска; D — коэффициент диффузии пара при температуре Т и барометрическом давлении P. Он рассчитывается по формуле
48
D =D0(Т/Т0)1,8(P0/P), |
(2.2.2) |
где D0 =2,16 10–5 м2/с — коэффициент диффузии молекул воды в воздухе при температуре T0 =273 К и нормальном давлении P0 =0,1 МПа. Эта формула согласуется с экспериментом в диапазоне температур 273–1493 К.
Результаты расчетов по формуле (2.2.1) и экспериментальные зависимости v–1 =ƒ(l) совпадают при ϕ<0,75. Это свидетельствует о том, что в этих условиях имеет место диффузия пара через газ, находящийся внутри капилляров. При влажности ϕ>0,75 в капиллярах с размерами d <30 мкм наблюдается пленочный перенос, а в капиллярах d >30 мкм он отсутствует (рис. 2.3). С увеличением температуры от 295 до 314 К скорость испарения возрастает.
Большинство технологических процессов, связанных с сушкой материалов, проходят при высоких температурах и низких значениях относительной влажности воздуха. В этом случае при расчетах переноса влаги следует учитывать только пароперенос в порах материала. При расчете массопереноса в грунтах, почвах и других материалах при температурах, меньших 300 К, и высокой относительной влажности воздуха необходимо учитывать пленочный перенос влаги.
Молекулы жидкости находятся в положении равновесия до тех пор, пока за счет соседних молекул не приобретут энергию, достаточную для разрыва молекулярных связей, и активированного скачка в свободную от молекул микрополость [24]. Таким образом, молекула жидкости находится в связанном («оседлом») состоянии в течение времени τ1 и свободном τ2 <<τ1. За время τ2 молекула совершает скачок. Общее время
τ τ1 =τ0exp(E/RT), |
(2.2.3) |
где τ0 — соответствует периоду тепловых колебаний молекул; Е — энергия активации для совершения скачка (кДж/моль).
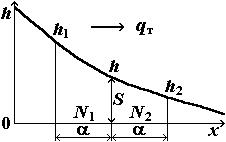
Толщина пленки снижается от мениска (x =0) до устья капилляра. В связи с этим возникает градиент толщины пленки dh/dx и соответствующий поток жидкости в пленке к устью капилляра q*.
Рассмотрим диффузию молекул жидкости через площадку S =ah, где а — ширина пленки; h — ее высота. Выберем толщину слоя молекул равной
|
|
|
средней длине скачка молекулы жидкости α. |
|
|
q* |
|
||
|
|
Количество молекул в левом N1 и правом N2 |
||
|
|
|
относительно площадки S объемах пропор- |
|
|
|
|
||
|
|
|
циональны, |
соответственно, αа(h +h1)/2 и |
|
|
|
αа(h +h2)/2 |
(рис. 2.4). В направлении оси x |
|
|
|
совершают активационные скачки 1/6 часть |
|
|
|
|
молекул в объеме. С учетом полученных со- |
|
Рис. 2.4. Схема для расчета мас- |
отношений найдем разность масс жидкости, |
|||
сопереноса в пленке жидкости |
которая переносится через площадку S: |
|||
|
|
|
49 |
|

|
|
M =(1/12)ρжαa(h2 −h1), |
(2.2.4) |
где |
ρж |
— плотность жидкости. Градиент |
толщины пленки |
– h/ |
x ≈– |
h/(2α), где h =h1 −h2. |
|
Разделим левую и правую части равенства (2.2.4) на Sτ и перейдем от конечных разностей к бесконечно малым. Окончательно получим
q* =−Dжρж(d(lnh)/dx), |
(2.2.5) |
где Dж — коэффициент диффузии влаги в пленке.
Полагаем, что толщина пленки h в пределах ее длины l* линейно уменьшается по высоте капилляра от мениска до конечной толщины h0 >0, соответствующей толщине адсорбированной пленки. Скорость переноса можно рассчитать по формуле:
vп =q*/ρж ≈Dж(lnh/h0)/l*, |
(2.2.6) |
где l* — длина водопроводящей пленки.
По мере уменьшения толщины пленки у устья капилляра (h →h0) скорость vп →0. Снижается также коэффициент диффузии Dж из-за увеличения энергии активации скачков молекул жидкости при взаимодействии их с центрами сорбции на поверхности стенки капилляра.
В гидрофобных капиллярах энергия взаимодействия между молекулами воды больше, чем с его стенкой, поэтому толстые пленки влаги не
|
образуются. |
|
|
|
Своеобразная |
гидрофобиза- |
|
|
ция внутренней поверхности стек- |
||
|
лянных капилляров происходит |
||
|
при испарении растворов солей. В |
||
|
зоне испарения у мениска концен- |
||
|
трация соли возрастает. Она со- |
||
|
осаждается на внутренней поверх- |
||
|
ности капилляра. Это затрудняет |
||
|
адсорбцию молекул воды на стенке |
||
|
по мере перемещения мениска в |
||
|
глубь капилляра. |
|
|
|
При |
осциллирующей трех- |
|
|
кратной |
смене |
относительной |
Рис. 2.5. Зависимость обратной скорости |
влажности воздуха в камере от 0,7 |
||
испарения воды v–1 (ч/см) из капилляров |
до 0,9 возникают соответствующие |
||
диаметром d =12 (1), 15 (2), 37 (3) мкм при |
изменения |
скорости |
испарения из |
переменных значениях относительной |
капилляров (рис. 2.5). При первом |
||
влажности воздуха от координаты отсту- |
цикле смены режима в капиллярах |
||
пающих менисков l (мм) (прямолинейным |
с диаметром 12 и 15 мкм длина |
||
участкам графиков и максимумам на них |
пленки l* соответственно увеличи- |
||
соответствует ϕ=0,9, а минимумам — 0,7) |
|
|
|
50 |
|
|
|
