
Литература от Абакумова ч2 / Исследование влияния ультразвуковых колебаний и различных полей на скорость массопереноса в строительных материалах
.pdfСодержание. |
|
Введение |
3 |
1. Теория |
4 |
2. Исследование влияния акустического и |
|
электромагнитного полей на скорость пропитки |
|
строительных материалов |
12 |
3. Исследования влияния электромагнитного |
|
поля и ультразвуковых колебаний на скорость |
|
сушки строительных материалов |
15 |
4. Обработка экспериментальных данных |
18 |
Литература |
19 |
Редактор Т.А.Стороженко. Подписано в печать_______
Формат 60х841/16. Усл. п.л.______. Уч.-изд.л.________
Тираж ______ экз. Печать опер., бум. Писч. Заказ______
Издательство ВСГТУ, г. Улан-Удэ, ул. Ключевская 40а.
Министерство образования Российской Федерации
ВОСТОЧНО-СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ
Исследование влияния ультразвуковых колебаний и различных полей на скорость массопереноса в строительных материалах
Методические указания к проведению комплекса лабораторных работ для студентов специальностей
260200, 290600, 290300, 290700
Издательство Восточно-Сибирского государственного технологического университета
Улан – Удэ - 2003
Лайдабон Ч.С. Исследование влияния ультразвуковых колебаний и различных полей на скорость массопереноса в строительных материалах. Методические указания к проведению комплекса лабораторных работ для студентов специальностей 260200, 290600, 290300, 290700
Рецензенты: Дамдинов Ц.Д., и.о.доц., Чимитов А.Ж., ст. преп.
кафедра ПСМИ ВСГТУ
Составители:
Составители: Лайдабон Ч.С.. к.ф.-м.н., доцент Антохонов В.Б., к.ф.-м.н., доцент
= выбираются линии сетки,
=добавляются легенды,
=подписиваются данные эксперимента.
Затем:
- Составляется вспомогательная таблица: y = 1 – m/m
-Строится экспоненциальная часть графика у(t) по приведенной выше схеме,
-Добавляются линии тренда экспоненциальной функции
споказом:
=уравнений линии на диаграмме,
=величины достоверности аппроксимации.
Литература
1. Бадмаев Б.Б., Лайдабон Ч.С., член-корреспондент АН
СССР Дерягин Б.В., Базарон У.Б. “ Сдвиговые механические свойства полимерных жидкостей и их растворов “. ДАН СССР, 1992 г., т. 322, N2, 307 - 311.
2.Laidabon Ch.S., Damdinov B.B., Alekseev Yu.S, Badmaev B.B. “Investigation of viscoelastic properties of impregnate solutions”. Proceedings of the XX session of the Russian Acoustical Society, Moscow, 2000, v.1, pp.48-5.
3.Damdinov B.B., Laidabon Ch.S., Badmaev B.B. Dynamical properties of impregnate solutions.// Proceeding of II Congress of Slovenian Acoustical society, 2000, (in print).
4.Ильюшин А.А. Механика сплошной среды. – М.: Издательство МГУ, 1990. – 310 с.
5.Тихонов А.Н., Самарский А.А. Уравнения математической физики. – М.:Наука, 1972. – 736 с.
6.Jost W., Diffusion in Solids, Liquids, Gases, Academic Press. – 1960. – 620 p.
7.Магдеев У.Х. Слоистые защитно – декоративные композиты. – М.: ЛИА – ПРЕСС, 1997. – 196 с.
1.Включают установку и поддерживают в сушильной камере постоянную температуру 700С ± 10,
2.Пропитанные водой образцы взвешивают и устанавливают на подставку,
3.Снимают зависимость массы m образцов от времени t,
4.Полученные данные записывают в таблицу 2.
Таблица 2. Зависимость изменения массы образца от времени
t, мин |
0 |
10 |
… |
tn |
m, г |
m0 |
m1 |
… |
mn |
m=m0-mn, г |
|
|
|
|
m/m, % |
|
|
|
|
5. Обработку лабораторных данных производится на компьютере ( см. п.4 ).
4. Обработка экспериментальных данных.
Для обработки экспериментальных данных из приведенных выше таблиц вводятся функции m/m в cтандартную программу “ Мастер диаграмм ” в Excel. При этом:
-Выбирается тип диаграммы ( точечная ),
-Выбирается вид ( плавные линии с экспериментальными тогчками ) ,
-В диапазоне данных выбирается ряд ( в строках или в столбцах ),
-В рядах печатается условия эксперимента,
-В параметрах:
=ставятся заголовки,
=отмечаются оси координат,
Введение.
В большинстве технологических процессов при производстве строительных материалов имеют места
тепломассоперенос, от скорости которого существенно зависят как качество материала, так и его себестоимость. Поэтому исследование различных внешних факторов на скорость тепломассопереноса имеет важное значение.
Строительные материалы, как правило, представляют собой пористо-капиллярные материалы. Довольно часто на практике требуется удаление влаги из них с последующей пропиткой их специальными составами, т.е. требуется сушка изделия и их пропитка. Например, бетонные конструкции, находящиеся в грунте, достаточно быстро теряет свои эксплуатационные свойства. В настоящее время нет технологии сушки бетонных изделий в построечных условиях и их поверхностной модификации. А подобные технологии и соответствующие оборудования на сегодняшний день чрезвычайно нужны. Другой пример. Древесина представляет собой традиционный строительный материал со многими положительными и уникальными свойствами. Но она очень чувствительна к воздействию внешней среды, легко подвергается воздействию различных микроорганизмов. Также, изделие, изготовленное из невысушенной древесины, по ходу эксплуатации и естественной сушки усыхает, что существенно снижает качество деревянного изделия. Подобные примеры можно привести и по другим строительным материалам. Для них необходимы две технологические процессы:
-сушка,
-пропитка специальными составами.
Процесс сушки представляет собой длительный и энергоемкий технологический процесс. Ускорение данного процесса за счет повышения температуры или другими приемами чревата множеством отрицательных следствий. Так, древесина деформируется, коробится и, что очень существенно, образуются трещины. Все эти последствия резко снижают качество изделия из древесины.

Пропитка строительных материалов является еще более трудным, сложным технологическим процессом. В большинстве случаев эта технология требует применения вакуума и избыточного давления, что существенно повышает себестоимость изделия.
Таким образом, при производстве строительных материалов или ремонте строительных конструкций в построечных условиях требуется и сушка и пропитка изделий. Поэтому студентам строительных специальностей, особенно, технологам, необходимо в вузе ознакомиться с современными достижениями по указанным направлениям, выполнить ряд лабораторных исследований.
Цель исследований.
Экспериментально исследовать влияние ультразвуковых колебаний и различных полей на массоперенос в различных строительных материалах. А также изучить механизм воздействия внешних факторов на процессы сушки и пропитки строительных материалов, ознакомиться с современной теорией по данным направлениям.
1. Теория.
Процессы сушки и пропитки материалов имеют одинаковую природу, они обусловлены явлениями само-, баро- и термодиффузии.
При наличии в пористой системе градиента концентрации grad с(r,t) в ней наблюдается самодиффузия, выражаемая законом Фика
ϑС = -D grad С
являются три пьезоэлектрические излучатели ( также не изображены на рис. 1 ) с резонансными частотами 2,8, 7,2 и 10,0 кГц, установленные в камере и работающие от того же генератора.
В качестве образцов строительных материалов надо взять кубики из: керамики 5*5*5 см, бетона 2*2*2 см и древесины ( сосны ) 2,5*2,5*5 см. В связи с тем, что керамика обладает устойчивой пористокапиллярной системой, она была взята в качестве базового образца – экспериментальной модели строительного материала, позволяющего многократную сушку, т.е. базовый образец первоначально взвешивался, а затем опускался в воду в течение двух дней – до полного поглощения им воды. Далее в эксперименте снимается зависимость изменения массы dm образца от времени при различных частотах электрических сигналов в интервале 0 – 20,0 кГц до достижения первоначальной массы.
Группа разбивается на подгруппы из 2-3 студентов. Каждая подгруппа исследует влияние ультразвуковых колебаний и электромагнитного поля на скорость сушки трех видов образцов. Таким образом, максимальное время выполнения подгруппой первого комплекса лабораторных работ составляет 20 часов:
-Первая работа – подготовка образцов и их насыщение водой– 2 часа,
-Вторая работа – сушка образцов без поля – 6 часов,
-Третья работа – сушка оразцов под действием
|
|
|
ультразвуковых колебаний – |
6 часов, |
|
||||
- Четвертая работа – сушка образцов в |
|
|
|
|
|||||
|
|
|
электромагнитном поле– 6 часов. |
|
|||||
3.3. Ход работы: |
|
|
|
|
|
|
|
||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2. Структурно-функциональная схема
лабораторной установки |
|
|
1 |
– камера для сушки |
5 - образец |
2 |
- потолок |
6 - шток |
3 |
– термометр |
7 - весы |
4 |
–задвижка |
8 - тепловентилятор |
|
|
9 - антенны |
В камере 1 с помощью тепловентилятора 8 и второго потолка 2 создается замкнутый поток горячего воздуха, температура которого регулируется с помощью задвижки 4 и фиксируется термометром 3.Исследуемый образец 5 строительного материала устанавливается на весы 7 через шток 6. При исследовании влияния электромагнитного поля на скорость сушки образцов электрические сигналы от генератора ( на рис. 2 не изображен ) подаются на антенны 9, а в случае с ультразвуковыми колебаниями источниками колебаний
где: ϑС – диффузионный поток, С – концентрация, D – коэффициент самодиффузии.
Диффузионный поток в гетерогенной системе также может быть вызван при воздействии многих факторов, не
имеющих прямой связи с потоком вещества. Такие процессы рассматриваются как перекрестные. В частности, существенными для поставленной нами задачи являются термомеханические процессы, а именно, явления переноса, происходящие из-за градиентов температуры T(r,t) и давления Р(r,t), в том числе капиллярного. В первом случае имеем явление термодиффузии, описываемое соотношением
ϑТ = -H grad T.
Во втором случае действие давления, которое рассматривается как сумма давлений от внешнего воздействия и давления от поверхностного натяжения, вызывает бародиффузию, которая подчиняется закону Дарси
ϑР = -K grad Р.
Совместное действие указанных выше факторов обобщается выражением
ϑ = ϑС +ϑТ +ϑР = -(D grad С + H grad T + K grad Р) ( 1 )
где: ϑ - результирующий диффузионный поток, D, H, K – коэффициенты, соответственно, самотермо- и бародиффузии, обусловленные градиентами, соответственно, концентрации или плотности С, температуры Т и давления Р. В общем случае Ррез рассматривается как сумма внешнего давления Рстат и давления, обусловленного особыми свойствами переносимой жидкости – явлениями поверхностного натяжения Рпн и облитерации Робл :
Ррез=Рстат+Рпн-Робл ( 2 )
Для решения уравнения 1 требуется дополнить его уравнениями неразрывности струи, теплопроводности и состояния жидкости. Но аналитически в общем виде данная задача в настоящее время не решена, но для одномерного

случая самодиффузии Джостом получено решение системы уравнений в двух формах:
|
|
4 |
∞ |
|
1 |
|
|
|
( 2 j + |
1)πx |
|
( 2 j +1)2 π2 D |
t |
|||||
c = c 1 |
− |
|
|
∑ |
|
|
|
sin |
|
|
exp − |
|
|
x |
|
. |
||
π |
2 j +1 |
h |
|
h |
2 |
|
|
|||||||||||
|
|
j=0 |
|
|
|
|
|
|
|
|||||||||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
j |
|
|
2( j +1)h / 2 − x |
|
|
|
|
|
|
||||
|
|
−1) |
|
+ erfc |
jh + x |
, |
( 3 ) |
|||||||||||
с = с ∑( |
|
erfc |
|
|
2 Dx t |
|
|
|||||||||||
j=1 |
|
|
|
|
|
|
|
|
|
|
|
2 Dxt |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где функция erfc – дополнительный интеграл вероятностей
|
2 |
∞ |
erfc( ς ) = |
∫exp( −ξ2 )dξ. |
|
|
π |
ς |
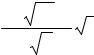
Из формулы ( 3 ) нами получена зависимость содержания массы в материале от времени:
|
|
|
t |
|
0,8 |
|
|
|
|
|
|
||||
M(t)=M* 1 |
−exp −8 D |
|
|
|
. |
( 4 ) |
|
h2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где: h –положение границы раздела фаз газ - жидкость, D – коэффициент самодиффузии,
М* - предельное значение массы жидкости в материале. Из уравнения 4 следует, что при наличии градиента концентрации в материале переносится масса, которая подчиняется экспоненциальному закону.
Подчеркнем, что данное уравнение справедливо для любого переноса массы в материале при наличии градиента концентрации, т.е. оно может быть применено как для сушки, так и для пропитки.
1.Высушенные образцы взвешивают и устанавливают в ванну с пропиточным составом,
2.Снимают зависимость массы m образцов от времени t,
3.Полученные данные записывают в таблицу 1.
Таблица 1. Зависимость изменения массы образца от времени
t, мин |
0 |
10 |
… |
tn |
m |
|
|
|
|
m=mn-m0 |
|
|
|
|
m/m |
|
|
|
|
4. Обработку лабораторных данных производится на компьютере ( см. п.4 ).
3. Исследования влияния электромагнитного поля и ультразвуковых колебаний на скорость сушки строительных материалов ( 20 часов ).
3.1.Оборудование и материалы. Установка для исследования влияния ультразвуковых колебаний и электромагнитного поля на скорость сушки строительных материалов, весы. Образцы - кубики из: керамики 5*5*5 см, бетона 2*2*2 см и древесины 2,*2,5*5,0 см.
3.2.Установка для исследования влияния ультразвуковых колебаний и электромагнитного поля на скорость сушки строительных материалов.
Лабораторная установка для исследования влияния электромагнитного поля и ультразвуковых колебаний на скорость сушки строительных материалов схематично изображена на рис. 2.
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис.1 Структурно-функциональная схема установки |
||
1 |
- |
насос |
5 - |
пропиточный состав |
2 |
- |
ванна |
6 - |
бетонная балочка |
3 |
- гидродинамический |
7 – система трубопроводов |
||
|
|
излучатель |
|
|
4 |
- |
поток жидкости |
8 - |
прокладки |
Группа разбивается на подгруппы из 2-3 студентов. Каждая подгруппа исследует влияние акустического и электромагнитного поля на скорость пропитки трех видов образцов одним из пропиточным составов, определяемым преподавателем. Таким образом, максимальное время выполнения подгруппой первого комплекса лабораторных работ составляет 20 часов:
-Первая работа – подготовка образцов и их сушка – 2 часа,
-Вторая работа – пропитка образцов окунанием – 6 часов,
-Третья работа – пропитка образцов в акустическом поле–
6часов,
-Четвертая работа – пропитка образцов в электромагнитном поле– 6 часов.
2.3. Ход работы:
Коэффициент диффузии D можно выразить через вязкость η жидкости и, пользуясь понятием подвижности b как коэффициентом пропорциональности между скоростью v и силой сопротивления F, действующей на движущийся
объект, пользуясь известным соотношением Эйнштейна D = kTb (где k – постоянная Больцмана; Т – абсолютная температура ) и формулой Стокса для шара F = 6πηrv ( где r – радиус шара ):
D = |
kT |
|
( 5 ) |
|
6πrη |
||||
|
|
|||
Коэффициент самодиффузии |
прямо пропорционален |
|||
температуре Т и обратно пропорционален динамической вязкости η.
С учетом ( 5 ) формулу ( 4 ) можно переписать в следующем виде:
|
|
|
Т t |
|
|
0,8 |
|
|
|
||
|
|
|
|
|
|||||||
M(t)=M* 1 |
− exp − const |
|
|
|
|
|
|
|
. |
( 6 ) |
|
|
|
|
2 |
|
|||||||
|
|
|
η h |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
Мы оценили вклад самодиффузии в процесс массопереноса в пористых материалах. В этом случае поток самодиффузии увеличивается с повышением температуры и снижением вязкости жидкости или раствора.
Подобным же образом можно оценить вклад бародиффузии в процесс массопереноса в изделии. Но в первом приближении выражение для потока бародиффузии можно получить, пользуясь формулой Пуазейля, как это сделано у Ю.М.Баженова:
πρ |
P r 3 |
t |
|
|
M(t)= |
0 |
( 7 ) |
||
η |
||||
2 |
|
|
Таким образом, мы получили искомый вклад бародиффузии. В данном случае мы имеем параболическую зависимость переносимой массы. Притом, со снижением вязкости жидкости или раствора повышается поток бародиффузии.
Таким образом, приведены решения уравнений диффузий в одномерном случае, которые нами использованы для описания процессов сушки и пропитки строительных материалов. Также получены выражения, связывающие коэффициенты диффузии со свойствами жидкостей и внешними условиями.
Из формул ( 6 ) и ( 7 ) следует, что при повышении температуры материала или жидкости, в соответствии с формулой ( 5 ), увеличивается коэффициент диффузии D, а также уменьшается вязкость η, что в конечном итоге приводит к увеличению вклада первого слагаемого уравнения ( 1 ) и, следовательно, к ускорению процессов сушки и пропитки материалов. Но, в этом случае, т.е. при повышении Т, вклад третьего слагаемого уравнения ( 1 ) в перенос массы уменьшается, вследствие того , что в этом случае снижается коэффициент поверхностного натяжения жидкостей σ. Таким образом, наиболее распространенный на практике метод ускорения массопереноса в материалах, за счет повышения температуры материала и жидкости, ограничен. Или другой, часто применяемый на практике пример, для пропитки пористо-капиллярных материалов и изделий используют вакуум и избыточное давление. Этот прием основан на том, что к Р ( 1 ) добавляется внешнее, статистическое давление. Третий прием: для увеличения глубины проникновения применяют маловязкие пропиточные составы. В этом случае используются дефицитные и дорогостоящие растворы, которые, для исключения обратного вытекания, вдобавок должны обладать полимеризующейся способностью. Все
Установка для исследования влияния акустического и электромагнитного полей на скорость пропитки строительных материалов ( рис.1 ) состоит из следующих узлов:
-Ванны для пропитки образцов строительных материалов,
-Гидродинамической системы для создания в пропиточном растворе акустического поля,
-Оборудования, создающего электромагнитное поле в пропитываемом изделии,
-Измерительного оборудования.
Вэкспериментах ( рис. 1 ) образцы 6 устанавливаются на прокладках 8 в ванну 2 с пропитывающим составом 5. Гидродинамическая система установки включает в себя насос 1, гидродинамический излучатель ( ГДИ ) 3 – источник акустических колебаний и систему трубопроводов 7, обеспечивающих работу установки. Скорость пропитки оценивалась взвешиванием образцов на весах с точностью до 0,1 %.
Вэкспериментах должны принимать участие параллельно три партии одинаковых образцов для каждого пропиточного состава: первая – контрольная, пропитывается простым окунанием, вторая – экспериментальная, пропитывается в акустическом поле (с применением ГДИ ), третья – в электромагнитном поле. Каждый эксперимент проводится в течение 90 минут. Скорость пропитки оценивается взвешиванием образцов –
определением относительного изменения массы m/m – привеса от времени.
Таким образом, имеются два фактора – объемная структура и меняющийся по толщине пристеночный слой жидкости, которые определяют скорость массопереноса в пористо-капиллярных телах: структура жидкости в объеме и структура в пограничном слое жидкости. В том и другом
случае их можно разрушить с помощью ультразвуковых колебаний или акустического и электромагнитного полей. При разрушении структуры жидкости происходит скачкообразное снижение вязкости жидкости, что повышает скорость переноса массы в теле, а разрушение структуры пограничного слоя – снятию облитерации капилляров, т.е. к восстановлению течения жидкости в них ( при этом снимается давление, противодействующее переносу массы ), что в конечном итоге должно привести к ускорению диффузии в пористо-капиллярных телах или к ускорению сушки и пропитки материалов.
2. Исследование влияния акустического и электромагнитного полей на скорость пропитки строительных материалов ( 20 часов ).
2.1.Оборудование и материалы. Установка для исследования влияния акустического и электромагнитного полей на скорость пропитки строительных материалов, весы. Образцы - кубики из: керамики 5*5*5 см, бетона 2*2*2 см и древесины 2,5*2,5*5,0 см. Пропиточные составы: вода, раствор пека в толуоле или дизельном топливе, антипирины, антисептики.
2.2.Описание установка для исследования влияния акустического и электромагнитного полей на скорость пропитки строительных материалов перечисленные методы ускорения массопереноса обладают
определенными недостатками, не обеспечивают быстрого и полного заполнения пор материалов.
Эффект влияния на скорость массопереноса в пористо-капиллярных телах в значительной мере зависит от факторов и явлений, протекающих в жидкостях и растворах.
К ним относятся понятие структуры у жидкостей и облитерация капилляров.
К идее ускорения массопереноса можно подойти с принципиально другой точки зрения – с позиций понятия структуры жидкости. Известно, что до сих пор окончательно не разработана общая теория жидкого состояния вещества. Если для газов и кристаллов имеются простые модели, соответствующие предельным случаям - идеальному газу и идеальному кристаллу, то для жидкостей не существует достаточно простой модели, на основе которой можно было бы строить теорию.
Строгая статистическая теория развита только лишь для простых жидкостей, но для реальных жидкостей она предсказывает упорядочение или ассоциацию молекул, образование макромолекул, т.е. появление в них некоторой структуры, что подтверждается рентгеноструктурным анализом. Тем более в настоящее время все большую популярность завоевывает ассоциированная, кластерная модель жидкости, признающая существование структуры в жидкостях. Можно экспериментально подтвердить наличие структуры у жидкости. Пусть жидкость находится между двумя параллельными плоскостями, одна из которых совершает колебательное движение в своей плоскости с некоторой частотой, а вторая – неподвижна. При наличии сдвиговой упругости, или то же самое – при наличии структуры вторая плоскость будет испытывать реакцию на колебание первой плоскости. Известным специалистом по физике жидкого состояния Б.В.Дерягиным было доказано наличие структуры у жидкости и соответствующее этому состоянию вязкости ηМ, называемой максвелловской, а при ее разрушении вязкость жидкости многократно ( десятки – сотни раз ) снижается. Так, вязкость ηЭ, определяемая с помощью вискозиметров, характеризует состояние жидкости с разрушенной структурой. Теория метода
позволяет вычислить частоту релаксации и максвелловскую вязкость жидкости.
Второй фактор, влияющий на скорость массопереноса – увеличение толщины пристеночного слоя жидкости или, что то же самое, уменьшение эффективного сечения капилляра при определенных условиях течения жидкости по ним, что и наблюдается на практике.
По классическому представлению, расход текущей жидкости по капилляру зависит только от параметров капилляра, вязкости жидкости и от перепада давления, но не зависит от времени. Но, экспериментально было обнаружено уменьшение скорости течения жидкости по капиллярам до полной остановки, что получило название облитерации капилляра. Например, по Кичину И.Н. для трансформаторного масла, истекающего через латунный капилляр длиной 0.2 мм и диаметром 0.12 мм под давлением 0.1 МПа, время полной облитерации составляет 80-90 с. Впервые в 1922 г. американские ученые Вильсон Р.Е. и Бернард Д.П. обнаружили явление закупорки капиллярных отверстий жидкостями в системе гидроавтоматики. Затем процесс закупорки (облитерации) капиллярных отверстий исследовали в 1946 г. Вовк Г.П., в 1951 г. Башта Т.М., в 1957 г. Кичин И.Н., в 1962 г. Погодаев Ф.Г. Несмотря на то, что работы выполнялись качественно, экспериментальные данные у разных авторов расходятся и количественно и качественно. Например, одни авторы утверждали, что вода не образует заращивания капилляров, а у других авторов - заращивание капилляров водой наблюдается. Или Вовк Г.П. утверждал, что заращивание жидкостью может происходить и без протока жидкости, а Погодаев Ф.Г. настаивал, что заращивание капилляров жидкостью наблюдается только при наличии протока этой жидкости. Поэтому в литературе появились экспериментальные факты закупорки капилляров, но не
были предложены механизм и теория данного явления. Этот феномен играет существенную роль в массопереносе и его необходимо учитывать при рассмотрении вопросов пропитки и сушки пористых материалов.
Известно, что скорости облитерации жидкости зависит от температуры, свойств материала и длины капилляров, также и от вязкости растворов.
При этом облитерация обладает двумя особенностями. После прекращения течения жидкости – “ запирания капилляра ” столб жидкости в капилляре выдерживает значительные статические давления. Так, “ запертый ” пирексовый капилляр диаметром 250 мкм и длиной 5 мм выдерживает статическое давление, созданное водой высотой h = 60 см. С уменьшением диаметра капилляра в 10 раз это давление увеличивается 6 – 7 раз. Из этого экспериментального факта можно сделать вывод о том, что облитерация в значительной мере тормозит перенос массы в пористо-капиллярных материалах, особенно, в капиллярах диаметром меньше 1 мкм. Попытка его ускорения с помощью вакуума и избыточного давления не может привести к значительному ускорению таких процессов, как сушка и пропитка строительных материалов.
Вторая особенность облитерации – ее чрезвычайная чувствительность к механическим колебаниям и вибрациям. Подобное действие на облитерацию оказывает также и электромагнитное поле.
