§ 6. Векторное произведение векторов 4
Векторы
называются упорядоченными, если указано
место каждого из векторов. Упорядоченная
тройка векторов
,
,
называется правой, если с конца вектора
поворот на меньший угол от вектора
к вектору
осуществляется против часовой стрелки.
В дальнейшем будем рассматривать только правые тройки базисных векторов.
Определение.
Векторным произведением вектора
на вектор
называется вектор
,
удовлетворяющий условиям
1)
вектор
направлен так, что
,
,
– правая тройка;
2)
,
;
3)
,
где
– угол между векторами
и
.
Геометрические свойства векторного произведения
1) Необходимым и достаточным условием коллинеарности двух ненулевых векторов является равенство нулю их векторного произведения.
2)
Модуль векторного произведения
численно равен площади параллелограмма,
построенного на векторах
и
.
Определение.
Ортом ненулевого вектора
называется единичный вектор, коллинеарный,
одного направления с вектором
.
3)
Если
– орт, а S
– площадь параллелограмма, построенного
на векторах
и
,
то имеет место равенство
.
Алгебраические свойства векторного произведения
1)
;
2)
3)
;
4)
.
Докажем
свойство 1. Если векторы
и
коллинеарны, тогда
,
то есть
.
Если векторы
и
не коллинеарные, то при очевидной
одинаковой длине
выполняется
,
иначе обе тройки векторов
,
,
и
,
,
были бы правыми, что невозможно в силу
их противоположной ориентации.
Упражнение. Доказать свойства 2) – 4).
Выразим
векторное произведение векторов
и
через их координаты. Имеем
.
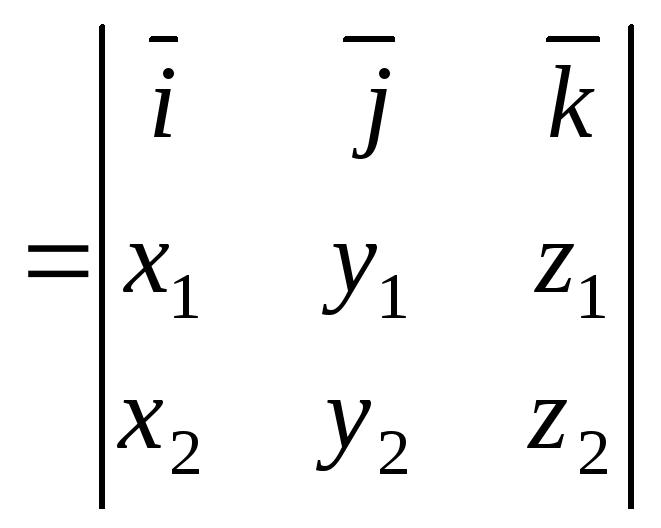При
доказательстве достаточно заметить,
что
,
,
,
,
,
,
,
,
.
Далее раскладывая определитель по
элементам 1-ой строки, получаем требуемое.
Если
векторы
и
коллинеарны, то их координаты
пропорциональны, то есть
.
Замечание.
Допускается иметь в знаменателе 0, если
всякую пропорцию
понимать как
.
Пример
IV.7.
Найти площадь треугольника АВС
с вершинами
,
,
.
Решение.
Воспользуемся свойством 4) векторного
произведения: площадь треугольника
равна половине площади параллелограмма,
построенного на векторах
и
.
Вычислим их векторное произведение,
имеем:
.
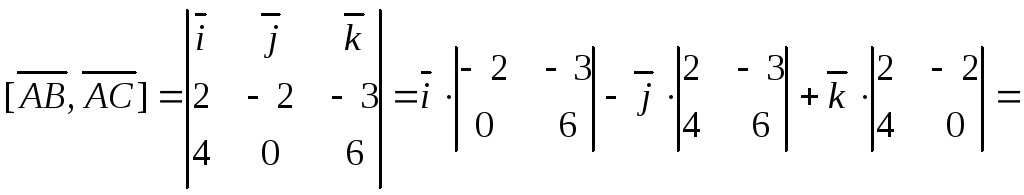
Площадь треугольника ABC равна половине величины этого векторного произведения:
кв.ед.
§ 7. Смешанное произведение векторов 4
Пусть
даны три вектора
,
,
.
Если
векторно умножить на
,
а затем скалярно на вектор
,
то получим число
,
называемое смешанным произведением.
Геометрически
смешанное произведение векторов
равно объему параллелепипеда, построенному
на этих векторах, если они образуют
правую тройку, и со знаком «»
в противном случае.
Выразим
смешанное произведение векторов
,
,
через их координаты, тогда имеем
.
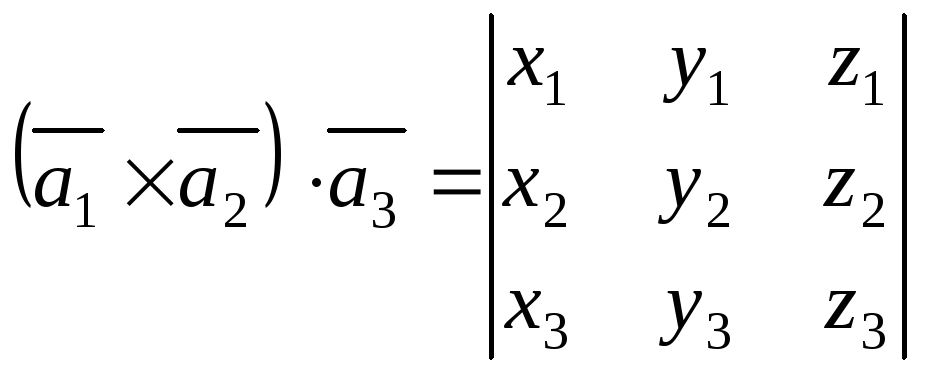(IV.14)
Для доказательства достаточно учесть
,
а затем разложить определить по 3-й строке и обнаружить совпадение.
Теорема IV.2. Необходимым и достаточным условием компланарности трех векторов является равенство 0 их смешанного произведения.
Следствие. Смешанное произведение трех векторов, два из которых совпадают, равно 0.
Для доказательства достаточно воспользоваться условием равенства 0 смешанного произведения и воспользоваться формулой (IV.14).
Пример
IV.8.
Найти объём тетраэдра, вершинами которого
являются точки
,
,
,
.
Решение.
Объём тетраэдра составляет шестую часть
объёма параллелепипеда, построенного
на векторах
,
и
.
Найдем смешанное произведение этих
векторов:
.
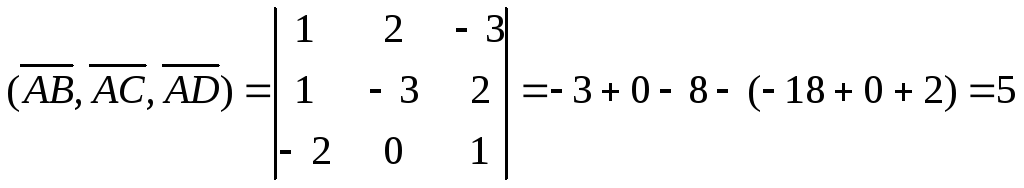Таким образом, объем тетраэдра равен
куб.
ед.