Суммы и произведения

Операции суммы и произведения относятся к основным алгебраическим операциям. Как правило, на практике приходится сталкиваться с многократными повторениями. Для удобства выполнений операций вводятся символы многократного повторения сложения – «» и умножения – «».

Пусть имеем конечное множество , тогда сумма его элементов записывается как, а произведение –, допускаются также обозначения   . Аналогичные вольности допускаются и при обозначении произведения элементов. Индексi называется скользящей переменной, которая может быть заменена любой другой буквой.

Пусть , тогда при необходимости двойной индексации можно ввести двойное суммирование, например,

.

Для двойной суммы выполняется аксиома коммутативности. В самом деле, имеем

.

Аналогично можно записать и произведение элементов с тем же свойством

.

Пример I.5. Раскрыть двойную сумму .

Решение. Имеем

.

Приближенные вычисления

Множество действительных чисел R широко применяется в математике и ее приложениях. В инженерных расчетах обычно конечный результат представляют в виде десятичной дроби. Но не каждое действительное число может быть точно записано в таком виде. К ним относятся все рациональные с периодом и все иррациональные числа. Их приходится округлять, то есть записывать приближенно. Для того, чтобы иметь n точных знаков после запятой, нужно вычислить не менее чем n+2 знака (т.е. дополнительно 2 разряда) и округлить по известным правилам.

Следует иметь в виду, что если приходится суммировать очень много слагаемых, то накапливается ошибка. Пренебрежение правилами округления, а иногда и при округлении с любой точностью, можно получить принципиально неверный результат. Особенно актуальна проблема оценки ошибок вычисления при нахождении корней уравнений и решения систем уравнений. Например, система уравнений не имеет решений (система несовместна), а при округлении правой части второго уравнениясистемаимеет множество решений.

При нахождении корней уравнения любое округление в сторону уменьшенияприводит к отсутствию действительных корней.

II. Элементы линейной алгебры § 1. Матрицы и определители 3, 7

Определение. Матрицей размера mn называется совокупность mn элементов, представленная в виде таблицы, состоящей из m строк и n столбцов

,

где – элемент матрицы A, стоящий на пересечении i-ой строки и j-го столбца, , , .

Матрица размера 1n или m1 называется матрицей-строкой или матрицей-столбцом соответственно (или вектором).

Если число строк матрицы равно числу столбцов, то матрица называется квадратной, а число строк называется ее порядком или размером. Матрица A порядка n имеет вид:

Элементы квадратной матрицы размера n, стоящие на пересечении строк и столбцов с одинаковыми номерами, то есть , , …, , образуют главную диагональ, а сумма элементов главной диагонали называется следом матрицы. Соответственно элементы , , …, , лежащие на прямой, соединяющей правый верхний и левый нижний углы матрицы, образуют побочную диагональ.

Мы будем рассматривать числовые и функциональные матрицы.

Определение. Матрица, все элементы которой равны нулю, называют нулевой.

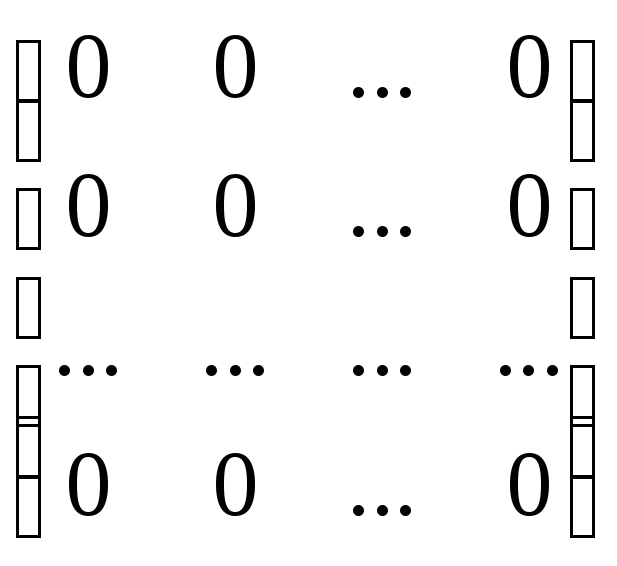
Определение. Квадратная матрица, у которой на главной диагонали стоят единицы, а остальные элементы равны нулю, называется единичной и обозначается

Определение. Квадратная матрица, у которой элементы, расположенные ниже главной диагонали, равны нулю, называется треугольной.

Определение. Матрица А^Т называется транспонированной к матрице A, если у нее каждая строка является столбцом матрицы A с тем же номером.