Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Псковский государственный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Бандурин TOE 1

.pdf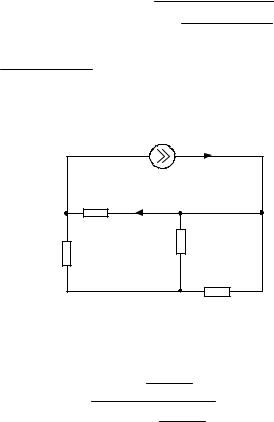

Скачиваний:

Добавлен:

15.03.2016

Размер:

2.08 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 227 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 > Следующая >>>

Рис. 4.8.

По

закону

Ома:

(E2 )

= 0,857 А,

тогда

R + 2R ×(3R + R)

2R + (3R + R)

(E2 )

= 0, 286 А.

= I2

2R + (3R + R)

Расчет подсхемы с источником тока J .

I4(J)

Рис. 4.9.

Узлы b и d объединяем, тогда по правилу разброса

(

)

3R + 2R × R

= J ×

2R + R

=1,571

А.

3R +

2R × R

R +

2R + R

Находим результирующий ток I4 ,

как алгебраическую сумму

частичных токов (частичный ток, совпадающий по направлению с

результирующим током, берем со знаком “+”):

I4 = I4( E1 ) - I4( E2 ) - I4( J ) = 0,143 - 0,286 -1,571 = -1,714 А.

Рассчитанный ток I4

совпадает с током I4 , найденным в п.2.

Используем метод преобразований

Для расчета тока I4 исходную схему относительно ветви ab преобразуем до одноконтурной схемы, в которой будет протекать искомый ток I4 .

Для этого преобразования проведем в несколько этапов. Вначале перенесем источник тока J на сопротивления ветвей ac и cd:

Рис. 4.10.

Затем преобразуем источники тока в ЭДС:

E3 = 3R × J = 600 В и E4 = R × J = 200 В.

Рис. 4.11.

Далее преобразуем параллельное соединение ЭДС и сопротивления ветвей bc и cdb:

Rэ		=		1			= 66,666 Ом;
					+	1
		1		2R
						R
Eэ	=		E2 + E4			- E1		× Rэ = 200 В.

					R

В результате получаем одноконтурную схему с искомым током I4 :

		Рис. 4.12.
Тогда по закону Ома:		−E3 − Eэ
	I4 =	−E3 − Eэ	= -1,714 А.
	R + 3R + Rэ
Найденный ток I4 совпадает с результатами п.2. и п.4.1.4.
Определяем ток в ветви ab методом эквивалентного генератора
Находим напряжение холостого хода U ( xx) в ветви ab.
					4
		Рис. 4.13.
По методу контурных токов:
		I22 = J ;
	(2R + R) × I11 - 2R × I22 = E1 - E2 ,
тогда I	= E1 - E2 + 2R × I22	=1 А; I ( xx) = I		22	− I = 2 −1 = 1 А.
11	2R + R	3		22	11
	2R + R

По 2 закону Кирхгофа: U4( xx)								= -3R × J - 2R × I3( xx) = -800 В, тогда
ЭДС эквивалентного генератора равна E									Г	= U ( xx) = −800 В.
									Г		4
Находим сопротивление эквивалентного генератора RГ :
				Рис. 4.14.
RГ = 3R + R × 2R = 366.666 Ом.
			R + 2R								(кз) эквивалентного гене-
Находим ток короткого замыкания										I	(кз) эквивалентного гене-
											4
ратора:
(кз)		= J Г		=		EГ		= -2.182 А.
I4		= J Г		=		RГ		= -2.182 А.
						RГ
Находим ток в ветви ab аналитически по двум формулам:
I4		=	EГ				= -1.714				А;
I4		=					= -1.714				А;
		RГ		+ R
I4	=		J Г					= -1.714			А.
I4	=		+	R				= -1.714			А.
		1	+	R	R
					R		Г
							Г
Находим ток в ветви ab графически:
				Рис. 4.15.
							64

Точка пересечения внешней ВАХ эквивалентного генератора с ВАХ резистора R = 100 Ом (U4 = R × I4 =100 × I4 В) дает решение:

I4 » -1,7 А.

Аналитический и графический расчет методом эквивалентного генератора позволяет найти ток I4 , который совпадает с результата-

ми п.2. и п.4.

Для контура без источника тока, например, bcdb строим потенциальную диаграмму. При этом обозначаем промежуточную точку k и принимаем потенциал точки b, как и в методе узловых потенциалов, равным нулю, т.е. ϕb = 0 .

Рис. 4.16.

Тогда при принятом обходе выбранного контура против часовой стрелки, проводим расчет потенциалов точек:

ϕc = ϕb - 2R × I3 = 0 - 200 × 0, 429 = -85,8 В;

ϕk = ϕc - R × I2 = -85,8 -100 × 0,143 = -100,1 В; ϕd = ϕk + E2 = -100,1 + 200 = 99,9 В;

ϕb = ϕd - E1 = 99,9 -100 = -0,1 » 0 ,

т.е. расчеты проведены верно, т.к. получилось ϕb » 0 и потенциалы точек ϕc и ϕd совпали с ранее найденными значениями в методе узловых потенциалов.

Следует отметить, что при расчете потенциалов точек напряжения и ЭДС берутся со знаком “+” в том случае, когда при обходе контура перемещаемся от “-” к “+”.

Строим потенциальную диаграмму: