
Бандурин TOE 1
.pdf
5.2. Метод преобразований (упрощаем исходную схему до одноконтурной)
|
2E1 2E2 11 R J |
|
|
I4 |
|
I4 |
1.714 |
|
|||
|
14 R |
|
|
5.3.Метод эквивалентного генератора
5.3.1.По методу контурных токов определяем токи ХХ
I22 |
J |
|
|
|
|
|
|
|
|
|
I11 |
|
E1 |
|
E2 |
2R I22 |
I11 |
1 |
|
||
|
|
2R |
R |
|
|
|||||
|
|
|
|
|
|
|||||
I3xx |
|
I22 |
|
I11 |
|
|
|
I3xx |
1 |
|
U4xx |
|
3R J |
2R I3xx |
Eg |
U4xx |
Eg 800 |
||||
5.3.2. Определяем сопротивление эквивалентного |
||||||||||
генератора Rг |
|
|
|
|||||||
Rg |
3R |
|
R 2R |
Rg |
366.667 |
|
||||
|
|
|
|
|
|
|||||
R2R
5.3.3.Определяем ток эквивалентного генератора Ig
|
Eg |
|
|
Ig 2.182 |
|
|
|
||||
Ig |
|
|
|
|
|
||||||
|
Rg |
|
|
|
|
|
|
|
|
|
|
5.3.4. Определяем ток I4 |
|
|
|
||||||||
I4 |
Eg |
|
I4 |
1.714 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Rg |
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
или |
|
|
|
||||
|
|
|
|
I4 |
Ig |
|
I4 |
1.714 |
|||
|
|
|
|
|
|
|
|||||
|
|
|
|
1 |
R |
|
|
|
|
||
|
|
|
|
Rg |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||
6. Находим ток I4 графически |
|
|
|
||||||||
стоим внешнюю характеристику генератора |
|
|
|||||||||
|
Ig |
0 |
|
|
|
|
|
1 |
BAXg 2 x |
||
BAXg |
|
|
BAX(x) linterp BAXg |
||||||||
0 |
Eg |
|
|
|
|
|
|
|
|
||
71

72

5. СИНУСОИДАЛЬНЫЙ ПЕРЕМЕННЫЙ ТОК
5.1. Действующие значения гармонических токов и напряжений
Действующие значения тока и напряжения характеризуют тепловое действие в линейном резистивном элементе с сопротивлением R. При токе и напряжении:
i = Im sin (ωt + α ), u = U m sin (ωt + α )
По закону Джоуля-Ленца:
T
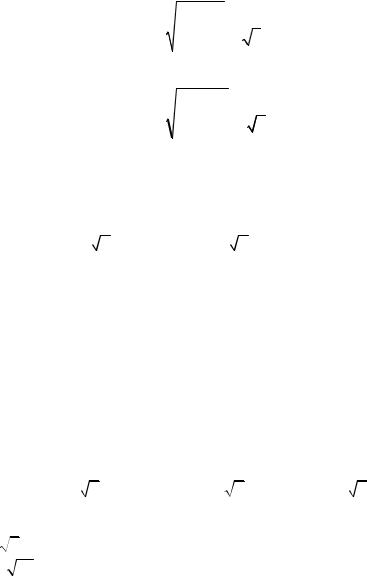
W = ∫i2R dt = I 2RT , Дж
0
T= 2π ω , с.
73
По закону Ома:
u = R × i, В .
Действующее значение тока
|
1 |
T |
I |
|
|
|
|
I = |
∫i2dt = |
m |
|
. |
|||
T |
|
|
|
||||
2 |
|||||||
|
0 |
|
|
||||
|
|
|
|
|
|
||
Действующее значение напряжения
|
1 |
T |
|
|
|
||
U = |
∫u2dt = |
U |
m |
|
. |
||
T |
|
|
|
||||
2 |
|||||||
|
0 |
|
|
|
|||
|
|
|
|
|
|
||
Действующее значение гармонического тока i численно равно такому постоянному току I, который за время T в том же сопротивлении R выделяет такое же количество тепла W. Действующие значения тока и напряжения не зависят от угловой частоты ω и начальной фазы α. В результате:
i = 
 2I sin (ωt + α ), u =
2I sin (ωt + α ), u = 
 2U sin (ωt + α ).
2U sin (ωt + α ).
5.2.Символический метод
Символический метод применяется для расчета линейных цепей с гармоническими токами и напряжениями. Этот метод основан на изображении гармонических величин комплексными числами. При этом проекция вращающегося вектора на любой из диаметров окружности, описываемая его концом, является гармонической функцией времени. Следовательно, синусоидальная величина может быть изображена вращающимся вектором на комплексной плоскости (рис. 5.1 а, б), причем этот вектор записывается в показательной,
тригонометрической и алгебраической формах.
i = Im sin (ωt + α ) = 
 2I sin (ωt + α ) = Im
2I sin (ωt + α ) = Im 
 2Ie j(ωt +α ) = Im
2Ie j(ωt +α ) = Im 
 2Ieɺ jωtIɺ= Ie jα = I cosα + jI sinα = a + jb ,
2Ieɺ jωtIɺ= Ie jα = I cosα + jI sinα = a + jb ,
где Im[
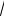 2 Ieɺ jωt ] – мнимая составляющая вращающегося вектора, j =
2 Ieɺ jωt ] – мнимая составляющая вращающегося вектора, j = 
 −1 – мнимая единица.
−1 – мнимая единица.
74

+ j = -1 |
+ j |
t = t1 |
ω |
|
ω |
|
|
|
|
|
ɺ jωt1 |
|
|
Ie |
α > 0 |
|
ωt1 + α |
а |
|
б |
|
Рис. 5.1. |
|
Iɺ– комплекс действующего значения тока.
Символический метод позволяет перейти от расчета линейных цепей с переменными во времени напряжениями и токами к расчету комплексной схемы замещения с постоянными напряжениями и токами. Для комплексных схем замещения справедливы все метод расчета, используемые при постоянных напряжениях и токах, но в комплексной форме.
5.3.Действия с комплексными числами
Где:
Fɺ = F × e jα = a + jb – комплексное число; F – модуль;
α – аргумент (фаза);
a – вещественная составляющая; b – мнимая составляющая.
1.Переход от алгебраической формы записи к показательной форме
a + jb Fe jα , где F = 
 a2 + b2 , α = (180 ) + arctg b . При этом a
a2 + b2 , α = (180 ) + arctg b . При этом a
180 градусов учитывается при a<0.
2.Переход от показательной формы записи к алгебраической форме
Fe jα a + jb ,гдеa=Fcosα, b=Fsinα.
75

3. |
Сложение и вычитание |
|
|
|
|
|
|
|
||||||||||||
|
F e jα 1 ± F e jα 2 |
= |
(a + jb ) ± (a |
2 |
+ jb |
) = (a ± a |
2 |
) + |
||||||||||||
1 |
2 |
|
|
|
1 |
|
|
1 |
|
2 |
|
1 |
|
|||||||
4. |
Умножение |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
(a + jb ) × |
(a |
2 |
+ jb |
) = .F e jα1 |
× F e jα2 |
= F F e j(α1+α2 ) |
||||||||||||||
1 |
1 |
|
|
|
|
2 |
|
|
|
1 |
|
|
2 |
1 |
2 |
|
|
|||
5. |
Деление |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
a + jb |
|
F e jα 1 |
|
|
|
F |
|
j(α 1−α2 ) |
= Fe jα . |
|
|
|
|||||||
|
1 |
1 |
= |
|
1 |
|
|
= |
|
1 |
e |
|
|
|
|
|
|
|||
a |
|
F e jα2 |
|
F |
|
|
|
|
|
|
||||||||||
|
+ jb |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2 |
2 |
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||
6. |
Возведение в степень |
|
|
|
|
|
|
|
||||||||||||
(a1 + jb1 )m = (F1e jα 1 )m = F1me jmα 1 = Fe jα . |
|
|
|
|||||||||||||||||
7. |
Некоторые соотношения |
|
|
|
|
|
||||||||||||||
j (b1 ± b2 ) = a + jb = Fe jα .
= Fe jα .
j = |
|
|
1 |
= − j; j3 = j. |
−1; j2 = 1; |
||||
|
|
|
j |
|
j = e j90 ; − j = e− j90 ; 1 = e j0 ; −1 = e j180 .
5.4.Действия с синусоидальными величинами
Рассмотрим действия с синусоидальными величинами, имеющими одинаковую угловую частоту ω.
1. Сложение
f (t ) = 
 2F sin (ωt + α ) = f1 (t ) + f2 (t ) ; f1 (t ) =
2F sin (ωt + α ) = f1 (t ) + f2 (t ) ; f1 (t ) = 
 2F1 sin (ωt + α1 ) ® Fɺ1 = F1e jα 1 ;
2F1 sin (ωt + α1 ) ® Fɺ1 = F1e jα 1 ;
f2 (t ) = 
 2F2 sin (ωt + α 2 ) ® Fɺ2 = F2e jα 2 ;
2F2 sin (ωt + α 2 ) ® Fɺ2 = F2e jα 2 ;
Для определения F и α используются: а) комплексные числа
F1e jα 1 + F2e jα2 = Fe jα определяются F и α; б) вектора на комплексной плоскости (рис. 5.2)
76

+j
Fɺ1
Fɺ = Fe jα
α1>
 α
α
0 α2>0 +1
Fɺ2
Рис. 5.2
2. Вычитание
f (t ) = 
 2F sin (ωt + α ) = f1 (t ) − f2 (t ); f1 (t ) → Fɺ1 = F1e jα 1 ;
2F sin (ωt + α ) = f1 (t ) − f2 (t ); f1 (t ) → Fɺ1 = F1e jα 1 ;
f2 (t ) → Fɺ2 = F2e jα 2 ;
а) комплексные числа |
|
|
|
F e jα 1 |
− F e jα2 |
= Fe jα |
определяются F и α; |
1 |
2 |
|
|
б) вектора на комплексной плоскости (рис. 5.3) |
|||
+j |
|
|
|
|
Fɺ1 |
Fɺ = Fe jα |
|
|
|
α1 |
α |
0 |
|
α2 |
+1 |
|
|
|
|
Fɺ2
Рис. 5.3
77

3. Дифференцирование
f (t ) = 
 2F sin (ωt + α ) → Fɺ = Fe jα ;
2F sin (ωt + α ) → Fɺ = Fe jα ;
df (t ) = 
 2ω F sin (ωt + α + 90 ) → ω Fe j(α +90 ) = jω Fɺ. dt
2ω F sin (ωt + α + 90 ) → ω Fe j(α +90 ) = jω Fɺ. dt
В результате при f (t ) ® Fɺ имеем df (t ) → jω Fɺ . dt
Таким образом, дифференцированию синусоидальной функции соответствует умножение изображающего ее комплекса на jω.
3. Интегрирование
f (t ) = |
|
F sin (ωt + α ) → Fɺ = Fe jα ; |
|
|
|
|||||||||
2 |
|
|
|
|||||||||||
|
|
|
F |
sin (ωt + α − 90 ) → |
F |
e j(α −90 ) |
|
|
|
|||||
∫ f (t )dt = |
|
2 |
= |
Fɺ |
. |
|||||||||
|
|
|
|
|
||||||||||
|
|
|
ω |
|
ω |
|
jω |
|||||||
В результате f (t ) → Fɺ |
имеем ∫ f (t )dt → |
Fɺ |
. |
|||||||||||
jω |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Таким образом, интегрированию синусоидальной функции соответствует деление изображающего ее комплекса на jω.
Закон Ома в комплексной форме
Закон Ома в комплексной форме основан на символическом методе и справедлив для линейных цепей с гармоническими напряжениями и токами. Этот закон следует из физической взаимосвязи между током и напряжением отдельных элементов цепи.
|
|
Iɺ |
|
|
R |
|
|
|
Резистивный элемент |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
UɺR |
|
|
|
Комплекс напряжения |
|
|
UɺR = R × Iɺ |
|
|
|||
78

|
+j |
|
Вектора напряжения и тока |
Iɺ |
UɺR |
+1
На комплексной плоскости вектор напряжения резистивного элемента совпадает по направлению с вектором своего тока.
|
|
|
|
jX L |
|
||
Индуктивный элемент |
|
Iɺ |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
UɺL |
|
||
Комплекс напряжения |
|
UɺL = jω L × Iɺ = jX L Iɺ |
|
||||
|
|
+j |
|
||||
|
UɺL |
|
|||||
Вектора напряжения и тока |
|
|
|
Iɺ |
|
||
|
|
|
|
|
|
|
|
+1
На комплексной плоскости вектор напряжения индуктивного элемента опережает по направлению вектор своего тока на 90 градусов.
|
|
ɺ |
|
|
|
|
− jX C |
||
|
|
|
|
|
|
||||
|
|
I |
|
|
|
|
|
|
|
Емкостный элемент |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Uɺ |
|||
|
|
|
|
|
|
|
С |
||
|
|
|
|
|
|||||
Комплекс напряжения |
UɺC = − |
|
j |
Iɺ = − jX C Iɺ |
|||||
|
|
||||||||
|
|
|
ωC |
||||||
79

+j
Iɺ
Вектора напряжения и тока |
+1 |
UɺC
На комплексной плоскости вектор напряжения емкостного элемента отстает по направлению от вектора своего тока на 90 градусов.
Где: XL=ωL – индуктивное сопротивление (Ом);
X C = |
1 |
– емкостное сопротивление (Ом). |
|
||
|
ωC |
|
Например, комплексная схема замещения цепи (рис. 5.4): jX L
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
Eɺ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
− jX C |
||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
Iɺ |
|
|
|
|
|||
|
|
Рис. 5.4. |
|
|
|
||||
|
|
|
|
|
|
|
Z = jX L + |
R(− jX C ) |
; Iɺ= |
Eɺ |
. |
|
|
|
|
|
|
|
R − jXC |
|
|||
|
|
|
|
|
|
|
|
|
Z |
||
Где: |
|
|
|
|
|
= Ze jϕ – эквивалентное комплексное сопротивле- |
|||||
Z = R |
+ jX |
Э |
|||||||||
Э |
|
|
|
|
|
|
|
|
|||
ние цепи (Ом); |
|
|
|
|
|
|
|
||||
Z = |
|
|
|
|
|
|
|||||
R |
2 + X |
2 |
– модуль сопротивления (Ом); |
||||||||
|
|
Э |
|
Э |
|
|
|
|
|
||
ϕ = arctg |
XЭ |
|
|
– |
аргумент (фаза) сопротивления (Град). |
||||||
RЭ |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||
80
