Бандурин TOE 1

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Псковский государственный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

= Ie jλ , I =

(RГ + R)2 + ( X Г + X )2

.pdf

Скачиваний:

Добавлен:

15.03.2016

Размер:

2.08 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 2210 11 12 13 14 15 16 17 18 19 20 21 22 > Следующая >>>

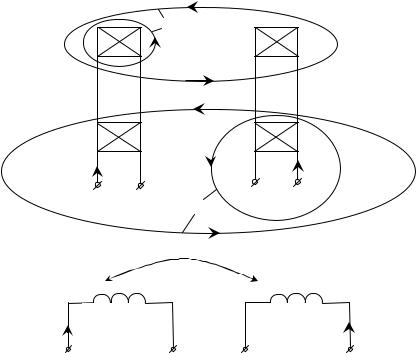
7. Встречное включение

		Φ11
		Φ21
		Φ12
i1		i2
i1		u2
		u2
		u1
	*	*
	*	Φ22
		Φ22
		Рис. 5.18.
		M

*	*
L1	L2	i2
i1		i2
u1	u2	+
+		+
	Рис. 5.19.

Включение двух катушек называется встречным, если их взаимные магнитные потоки Ф12 и Ф21 направлены навстречу друг другу. При этом токи катушек i1 и i2 ориентированы различным образом относительно одноименных зажимов (*).

Напряжения:

u = W

d (Ф11 − Ф12 )

= L

di1

− M

di2

1 dt

= W

d (Ф22 − Ф21)

= L

di2

− M

di1

2 dt

При гармонических токах и напряжениях:

Uɺ

= jω L Iɺ

− jωMIɺ

= Uɺ

+ Uɺ

1 1

Uɺ

= jω L Iɺ

− jωMIɺ

= Uɺ

+ Uɺ

2 2

Где Uɺ

= − jωMIɺ

= − jХ

Iɺ , Uɺ

M 2

= − jωMIɺ

= − jХ

Iɺ

M 1

ставляющие, обусловленные взаимной индуктивностью.

(5.13)

(5.14)

– со-

			+j
					ɺ		UɺM 2
					U L
					2
UɺM	Uɺ				Uɺ	2	Iɺ
1	L1						Iɺ
	Uɺ1						1
	Uɺ1
							+1
					Iɺ2
			Рис. 5.20.
При встречном включении составляющие напряжений взаим-
ной индукции Uɺ	и Uɺ		отстают от токов их создающих					Iɺ	и	Iɺ
M	M	2						2		1
1		2
соответственно на 90˚.
Последовательное соединение индуктивно связан-
			ных элементов
к	jX L2			d	R2
к
	Uɺ		2		ɺ
					U R
			jX M		2
			jX M
Eɺ
	UɺR1				Uɺ1
а	R1			b	jX L1		с
а

			Рис. 5.21.
Для схемы, изображенной на рис. 5.21 запишем уравнения по
первому закону Кирхгофа			Iɺ1 = Iɺ2 = Iɺ
			Iɺ1 = Iɺ2 = Iɺ
и по второму закону Кирхгофа
	Eɺ = UɺR			+ Uɺ1 + UɺR + Uɺ2
			1		2
				92

или

Еɺ = R Iɺ+ ( jХ

Iɺ

± jX

Iɺ) + R Iɺ+ ( jХ

Iɺ± jX

Iɺ) .

результате

Iɺ =

Eɺ

; X M = ω M , где

+ R2

+ j( ХL

+ ХL ± 2 X M )

знак «+» – согласное включение, знак «-» –

встречное включение.

В результате больший ток Iɺ соответствует встречному вклю-

чению.

Согласное включение (+)

Uɺ

UɺM 2

Eɺ

UɺL

Uɺ

UɺR2

U 1

UɺL1

Iɺ = Ie j 0°

а	UɺR	b	+1
	1
			Рис. 5.22.

9. Встречное включение (-)

+j					Uɺ
					М2
				Uɺ	к
				Uɺ	2
			UɺМ	1	UɺL
				1	2
Uɺ			c	Eɺ	d
Uɺ	1			Eɺ	UɺR2
	1
			UɺL
		1
а

		b			+1
UɺR		b			+1
1

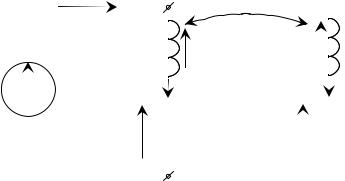
Рис. 5.23.

Параллельное соединение индуктивно связанных элементов

Iɺ			jX М		jX L2
Iɺ			jX М
jX L1		Uɺ1	Uɺ2
Eɺ	Iɺ1			Iɺ2
Uɺ		R1	UɺR		R2
R			2
1

Рис. 5.24.

Для схемы, изображенной на рис. 5.24 запишем уравнения по первому закону Кирхгофа

и по второму закону Кирхгофа

Eɺ = Uɺ

+ Uɺ

= R Iɺ

+ ( jX

Iɺ

± jX

Iɺ ) ,

1 1

Eɺ = Uɺ

+ Uɺ

= R Iɺ

+ ( jX

Iɺ

± jX

Iɺ

) .

2 2

M 1

В результате:

- (± jX

)

- (± jX

)

Iɺ1

× Eɺ

; Iɺ2 =

× Eɺ;

Z1Z 2 + X M2

Z1 Z 2 + X M2

+ Z

- 2(± jX

)

Iɺ=

× Eɺ.

Z1 Z 2

+ X M2

Развязка индуктивной связи

Развязка индуктивной связи применяется для ее исключения с целью упрощения расчетов и может быть доказана при помощи законов Кирхгофа в комплексной форме.

Два индуктивно связанных элемента подходят одинаковым

образом к общему узлу (d)

jX L

j( X L

− ХМ )

jX М

jX L2

j( X L2

− ХМ )

Рис. 5.25.

Два индуктивно связанных элемента подходят различным

образом к общему узлу (d)

j( X L

+ ХМ )

jX М

− jX М

+ Х

jX L

j( X

)

Рис. 5.26.

После развязки индуктивной связи для расчета цепи можно

использовать любой известный метод в комплексной форме.

Пример:

Z 1

Z М

Eɺ

Jɺ

Iɺ

Рис. 5.27.

Дано:

Eɺ = Ee jα , Jɺ = Je jβ ,

Z 1 = R1 + jX1 , Z 2 = R2 + jX 2 , Z = R + jX , Z М = jX М .

Определить: Iɺ = ?

После развязки:
Z 1	− Z М	с	Z 2 − Z М
а		с	b
		Z М
Eɺ		d	Z
Eɺ
		Jɺ	Iɺ
		Jɺ
		к
		Рис. 5.28.
Используем метод эквивалентного генератора (рис. 5.29):
Z 1	− Z М	с	Z 2 − Z М
а		с	b
		Z М
Eɺ		d	Uɺxx
Eɺ
		Jɺ
		к
		Рис.5.29.
Напряжение холостого хода:
EɺГ = Uɺxx = Eɺ + Jɺ× (Z1 - Z M ) = EГ e jα Г .
Сопротивление генератора:
Z Г = (Z 2 - Z M ) + (Z1 - Z M ) = RГ + jX Г = Z Гe jα Г .
Ток в нагрузке:

Активная мощность, потребляемая нагрузкой (рис. 5.30):

P = I 2 R =

EГ2 R

+ X )2

= f ( R)

+ R )2 + ( X

P = f (R)

Рис. 5.30.

Сопротивление, при котором активная потребляемая мощность

в нагрузке будет максимальной:

= R

+ ( X

+ X )2

, P =

EГ2

+ R )2

Пример:

Z 3

I33

Iɺ

Z M

Jɺ

Iɺ2

Eɺ

Iɺ

Iɺ22

Z н

Z 2

Iɺ

U J

Рис. 5.31.

Дано:

Eɺ, Jɺ, Z 1, Z 2 , Z 3 , Z М , Z н.

Определить: Iɺ, Iɺ1, Iɺ2 , UɺJ = ?

По методу контурных токов:

Iɺ33 = Jɺ,

Iɺ11(Z1 + Z 3 ) - Iɺ22 Z M - Iɺ33 Z 3 = Eɺ,

Iɺ22 (Z 2 + Z Н ) - Iɺ11 Z M - Iɺ33 × 0 = 0.

Далее находим:

Iɺ1 = Iɺ11; Iɺ2 = Iɺ22 ; Iɺ = Iɺ11 − Iɺ33 ; UɺJ = Eɺ − IɺZ 3 .

ЗАДАНИЕ №2

Линейные электрические цепи с гармоническими напряжениями и токами

Для заданной схемы с источниками гармонических ЭДС и

тока

e1(t) = 2E1 sin(ωt + α1); e2 (t) = 2E2 sin(ωt + α 2 );

e3 (t) = 0; J (t) = 2J sin(ωt + β ),

принимая ω = 314 рад/с и M=L/2 , выполнить следующее.

Записать систему независимых уравнений по законам Кирхгофа для мгновенных значений токов.

Рассчитать без учета M комплексные сопротивления ветвей, соединяющих узлы, помеченные на схеме буквами и изобразить комплексную схему замещения с этими сопротивлениями для расчета комплексов действующих значений токов ветвей (номера и направления токов сохранить согласно заданию №1, причем параллельное соединение R и С представить в виде одного комплексного сопротивления).

Не исключая индуктивной связи, определить комплексы действующих значений токов всех ветвей и напряжение на зажимах источника тока:

по законам Кирхгофа, методом контурных токов.

Записать мгновенные значения тока в ветви ab и напряжения на зажимах источника тока.

Рассчитать балансы активной и реактивной мощностей.

Построить лучевую диаграмму токов и совмещенную с ней топографическую диаграмму напряжений.

Определить показание вольтметра.

Сделать развязку индуктивной связи и по методу эквивалентного генератора относительно сопротивления R ветви ab определить комплексное сопротивление активного двухполюсника (эквива-

лентного генератора) Z Г = Z Г × e jϕ Г , ЭДС генератора EɺГ и ток Iɺab в ветви ab, а затем при изменении сопротивления R ветви ab от 0 до 10 × Z Г рассчитать и построить зависимость для активной

мощности Pab = f ( R) .

Проанализировать результаты вычислений и сформулировать выводы по заданию.

Примечание: Схемы и таблицы к заданию №2 приведены в задании №1.

Методические указания к работе № 2.

Для заданной схемы дано: e1(t) = 2 × E1 × sin(ωt + α1) , В;

e2 (t) = 2 × E2 × sin(ωt + α2 ) , В; e3 (t ) = 0 , В;

J (t) = 2 × J ×sin(ωt + β ) , А.

E1		E2	J	α1		α 2	β
В		В	А	град		град	град
100	200		2	90		0	-60

R		L	C			ω	M
Ом		мГн	мкФ		рад/с		мГн
100		318,47	31,8		314		L 2

Схема:

Рис. 6.1.

Записываем систему независимых уравнений по законам Кирхгофа для мгновенных значений токов (функций времени). Для этого указываем номера и направления токов в ветвях схемы аналогично заданию 1. Так как e3 (t) = 0 , то узлы a и m, k и c объединяем. В результате полученная схема будет иметь: nу = 4 узла, nв = 7 ветвей;

n1 = nу − 1 = 3 уравнений по первому закону Кирхгофа, n2 = nв − n1 = 4

уравнений по второму закону Кирхгофа.

Выбираем 3 узла (например, a, b, d) и 4 контура, для которых составляем уравнения по законам Кирхгофа, учитывая, что индуктивно связанные элементы включены встречно:

узел a: J (t ) + i4 − iR − iC = 0 ,

узел b: i1 + i3 − i4 = 0 , узел d: −i1 − i2 − J (t ) = 0 ,

∫

контур:

3R × iR -

× dt = 0 ,

контур:

∫

iC dt + Ri4 + L

di4

- M

di3

+ L

di3

- M

di4

+ 2Ri3 = 0 ,

контур: -R ×i2

- 2R ×i3

- L

di3

- M

di4

= e1(t) - e2 (t) ,

- L

контур: -R ×i4

di4

- M

di3

= uJ (t) - e1(t) .

100

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 2210 11 12 13 14 15 16 17 18 19 20 21 22 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
19.09.201948.93 Кб3АЯ 0762 Экзамен 2008г.docx
#
19.09.201950.08 Кб2АЯ 0762 Экзамен Актуальная версия.docx
#
11.11.2019223.23 Кб8Б3. Б4. История мировой (античной) рабочая прог...doc
#
11.11.2019183.3 Кб4Б3.Б 1_Введение в спецфилологию.ЕВК.ИВМ.doc
#
11.11.2019143.87 Кб6Б3.Б6. Древнерусская литература.doc
#
15.03.20162.08 Mб45Бандурин TOE 1.pdf
#
15.03.20167.22 Mб37Бандурин TOE_2.pdf
#
15.03.2016789.99 Кб80Бандурин Методичка расчет ПП.pdf
#
15.03.2016454.37 Кб70Бандурин Методичка расчет эм полей.pdf
#
15.03.20166.58 Mб52Бандурин Теоретич основы электротехн Теория электрич цепей электромагн поля С.А.Башарин 2004.djvu
#
15.03.20162.76 Mб737Бандурин ТОЭ-3 лекции.docx