Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Псковский государственный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Бандурин TOE_2

.pdf

Скачиваний:

Добавлен:

15.03.2016

Размер:

7.22 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 203 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 > Следующая >>>

B = uC 2

(0+ ) − uC 2

пр

= −66, 666 В.

Записываем окончательный результат

(t) = u

+ Bеpt = 100 − 66, 666е−33,333t

В.

C 2

C 2пр

τ =

= 0, 03 с,

= 5τ = 0,15 с,

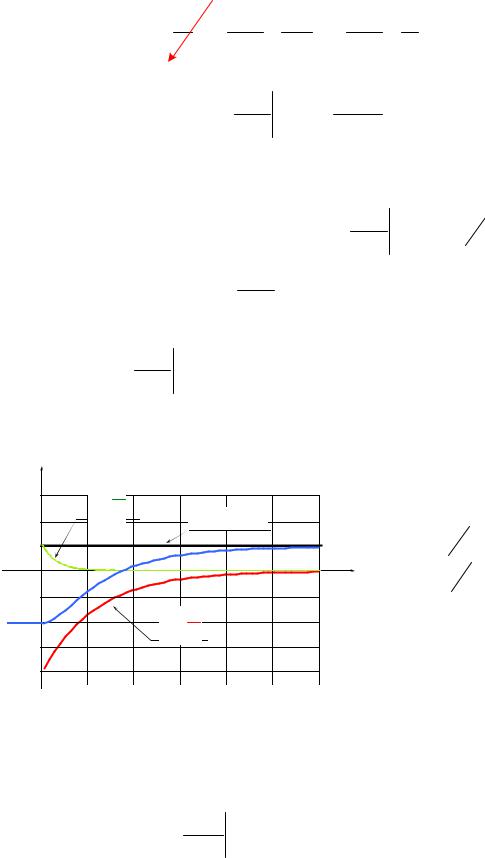
B uС2 (t)

120

uС2 (t)

uС2 (0+ )

2τ

3τ

4τ

5τ

-40

−

) -80

-120

Рис. 24

Расчет переходных процессов в цепях 2-го порядка

классическим методом

Цепь 2-го порядка после коммутации содержит:

-L и С,

-или две L,

-или две С.

Характеризуется уравнениями:

а		d 2 f (t)		+ а	df (t)	+ a		f (t) = F (t) ,
	2						0
		dt	2	1	dt

f (t) = fпр (t) + fсв (t) ,

где f (t) – напряжение или ток переходного процесса, а0 , а1, а2 – постоянные коэффициенты.

F (t) – функция, определяемая источниками после коммутации, fпр и fсв – принужденная и свободная составляющие.

Характеристическое уравнение: a2 p2 + a1 p + a0 = 0 . Корни характеристического уравнения

	a		a2		a
p = −	1	±	1	−	0	.

1,2	2a2		4a22		a2

В зависимости от корней характеристического возможны следующие виды переходных процессов:

•	a2			a
	Если	1	>	0	– кони вещественные, отрицательные и разные.

	4a22			a2

Апериодический режим

fсв(t)

А2

св

(t) = A e p1t

+ A e p2t

+ ... + A e pnt ,

А еp2t

fсв(t)

τ1

, τ 2 =

– постоянные времени,

А ер1t

tп = 5 max(τ1,2 ) – длительность

переходного процесса.

А1

tп = 5τ1

Рис. 25

•

Если

Корни вещественные отрицательные и равные.

4a22

Критический режим,

fсв(t)

св

(t) = ( A + A t + ... + A t n−1 ) e pt ,

fсв(t)

p = p = p = −

2a2

tп

tп =

– длительность переходного

процесса.

Рис. 26

•

Если

Корни

комплексно-

сопряжённые, с

4a22

отрицательной вещественной частью.

Колебательный режим или периодический режим

f (t)

fсв (t) = A e

−δ

свt

соs(ωсвt + α ) ,

св

где p1,2

= −δсв ± jωсв

огибающая

Аcos α

δсв =

–

коэффициент затухания

2а2

fсв(t)

свободных колебаний,

а2

ωсв =

−

– угловая частота

а2

4а22

Tсв

касательная

свободных колебаний,

Рис. 27

Тсв = 2π ωсв – период свободных колебаний,

τ= 1δсв (с) – постоянная времени огибающей свободных колебаний,

tп = 5τ (с) – длительность переходного процесса, А, α – постоянные интегрирования.

Пример

Дано:

E = 100 В, J = 2 А,

e u

L = 6, 25

Гн, С = 100 мкФ,

L uC

R = 100

Ом .

iС

Определить:

i(t) = ?

Рис. 28

Для схемы после коммутации по законам Кирхгофа составляем уравнения

−i − J + iL + iC = 0 ,

(1)

u = u

= L

diL

(2)

e = R i + uC ,

(3)

причём

= C

duC

(4)

Из уравнений 3 и 4: i

= C

duC

= C

d (e − R i)

= С

− R C

. (5)

Из уравнений 2 и 3:

i =

∫

u dt =

∫

u dt =

∫

(e − R i) dt .

Из уравнений 1, 5, 6:

−i − J +

∫(e − R i)dt +С

− R C

= 0

Продифференцируем уравнение 7:

−

i + С

d 2e

− R C

d 2i

= 0

dt2

L L

dt2

В результате из уравнения 8:

R C

d 2i

i =

+ C

d 2e

−

dt2

Или F (t) =

+ C

d 2e

−

, где – а

= R C , а

= 1, а

dt2

Решение уравнения 9: i(t) = iпр (t) + iсв (t) . Т.к

e = 100 = const1 ,

J = 2 = const2 , то iпр (t) = Iпр = const3 . Подставим Iпр в уравнение 9:

d 2 Iпр

dIпр

Iпр

+ C

d 2e

−

dt 2

dt2

Тогда Iпр

= 1.

iпр (t) = Iпр

(6)

(7)

(8)

(7)

можно также найти из расчета установившегося режима после

коммутации (t = ∞) . По 2 закону Кирхгофа e = R I

пр

, I

пр

= e

= 1 А.

Характеристическое уравнение RCp2 + p +

= 0 ,

(10)

= −20 (1

) ,

) –

p1,2 = −

−

), р1

р2 = −80

2RC

апериодический переходный процесс. Уравнение (10) можно также получить из Z(p)=0 после коммутации.





pL	1
pL
	рС	Z(p)
	Рис. 29	Z(p)

Z ( p) = R + pL 1 pC = 0 pL + 1 pC

или

RCp2 + p + R = 0 . L

При апериодическом переходном процессе i (t) = A e p1t + A e p2t										тогда
						св	1		2
i(t) = i (t) + i (t) = 1 + А е−20t + А е−80t .
пр	св	1	2
Для определения А и А найдем i(0					) и	di(t)		– это зависимые
						di(t)
				+
	1	2		+		dt
						dt		t =0+
								t =0+

начальные условия.

Определяем независимые начальные условия: iL (0− ) и uC (0− ) .

	R		J
		+

			С


e		uC
e		uC

i( 0− )

Рис. 30

Схема после коммутации при t = 0+

	R	J
		J
		ЕC
e	JL

iC (0+ )

i(0+ )

Рис. 31

iL (0− ) = 0 ,

uC (0− ) = e + RJ = 300 В,

причём

i(0− ) = −J = −2 А.

J L = iL (0− ) = iL (0+ ) = 0 ,

EC = uC (0− ) = uC (0+ ) = 300 В,

По 2 закону Кирхгофа e − EC = R i(0+ ),

тогда i(0+ ) = e − EC = −2 А.

Для определения di(t)

dt t =0+

используем уравнение 3 e = R i(t) + uC

которое продифференцируем

de = R di(t) + duC = R di(t) + iC

т.е.

di(t)

= − iC (0+ ) .

t =0+

iC (0+ ) найдем по 1 закону Кирхгофа

−i(0+ ) − J + J L + iC (0+ ) = 0

iC (0+ ) = i(0+ ) + J − J L = −2 + 2 − 0 = 0 , тогда di(t)

= 0 (А

) .

t =0+

Т.о. i(t) = 1 + A e−20t + A e−80t

, di(t) = −20 A e−20t − 80 A e−80t .

i(0+ ) = 1 + A1 + A2

= −2;

А1 = −4

→

( А);

Или при t = 0+ di(t)

= −20 A1

− 80A2 =

А2 = 1 ( А).

t =0+

Окончательный результат i(t) = 1 − 4e−20t + 1e−80t , А.

i(t)

- t

1е τ1

iпр(t) = 1 A

= 5 10−2

i(t)

с,

= 1, 25 10−2

с,

×10

−2

-1

tп = 5max(τ1,2 ) = 5 τ1

i(0− )

- t

-3

-4e τ 2

= 25 10−2 с.

-4

Рис. 32

Порядок расчета переходных процессов в цепях 2-го порядка с

постоянными или периодическими источниками

• Для искомого напряжения или тока

f (t) определяются начальные

условия f (0+ ) и df (t)

t =0+

•	Определяется принужденная составляющая	fпр (t) .
•	При помощи Z ( p) = 0 находятся корни	характеристического
	уравнения.

•	В зависимости от p1 и p2 записывается			fсв(t) .
•	По начальным условиям f (0+ )	df (t)		и находятся постоянные

		dt
			t =0+
	интегрирования.

•	Записывается окончательный результат			f (t) = fпр (t) + fсв (t) .

Операторный метод расчёта переходных процессов

Операторный метод (преобразование Лапласа) расчета переходных процессов используется для того, чтобы обыкновенные дифференциальные уравнения с постоянными коэффициентами (в пространстве оригиналов) преобразовать в алгебраические (в пространстве изображений). Очевидно, что алгебраические уравнения решаются проще. После решения алгебраического уравнения над полученной функцией (изображением) производится обратное преобразование Лапласа, получается оригинал. Полученный оригинал – это функция, которая и будет решением дифференциального уравнения.

Любой функции можно сопоставить её преобразование Лапласа

∞

F ( p) = ∫ f (t)e− pt dt ,

где F ( p) – изображение, f (t) – оригинал.

Приведём изображение нескольких часто встречающихся функций. Определим изображение константы – f (t) = A (const) :

∞

− pt

0∞ =

F ( p) = A∫ e− pt dt = −

Найдем изображение экспоненциальной функции –

f (t) = eαt :

∞

−( p −α)t

F ( p) = ∫ eαt e− pt dt = −

0∞ =

p − α

Изображение экспоненциальной функции поможет нам найти изображения синусоидальной косинусной функций – sin(ωt), cos(ωt) . Для этого запишем эти функции через формулу Эйлера. Далее осуществляем следующую цепочку преобразований:

sin(ωt)

cos(ωt)

= e jωt − e− jωt

2 j

= e jωt + e− jωt

→

−

2 j p − jω

p + jω 2 j

→

2 p − jω p + jω

p + jω − p + jω

;

+ ω

p + jω + p − jω

+ ω

Определим изображение производной

df (t)

функции f (t) , имеющей

изображение F ( p)

∞

df (t)

∞

0∞

∞

∫

e− pt dt = ∫ e− pt df (t) = f (t)e− pt

+ p ∫

f (t)e− pt dt = − f (0) + pF ( p) .

И, наконец, определим изображение интегрального выражения∫ f (t)dt

∞

e− pt ∫ f (t ')dt '

∞

∫ f (t)e− pt dt

F ( p)

∫

∫ f (t ')dt ' e− pt dt = −

∫

∫ f (t ')dt ' d (e− pt )=

Таблица преобразований Лапласа
	f (t) -оригинал	F ( p) -
		изображение
1		1 p

			eαt	1 ( p − α)
			e−αt	1 ( p + α)
			sin(ωt)	ω (p			− ω	)
			sin(ωt)			2	2

			cos(ωt)	p (p			+ ω	)
			cos(ωt)			2	2

			df (t) dt	− f (0) + pF ( p)

			t		F ( p)
			∫ f (t)dt
			∫ f (t)dt			p
			0			p
			0
Для определения оригинала f(t) используется обратное
преобразование Лапласа
	1	δ + j∞
f (t) =	1	∫ F ( p) e pt dp – обратное преобразование Лапласа.
f (t) =	2π j	∫ F ( p) e pt dp – обратное преобразование Лапласа.
	2π j	δ − j∞
		δ − j∞

На основании обратного преобразования Лапласа получена

D( p)

+ d p + d

p2 + ... + d

теорема разложения.

Если F ( p) =

B( p)

b0 + b1 p + b2 p2 + ... + bn pn

причем:

•

m<n;

•

корни B(p)=0 различны;

•

корни D(p)=0 и B(p)=0 различны.

D( p к )

тогда f (t) = ∑

e p к t , где pк

– корни B(p)=0

к=1

B '( p к )

B' ( p

) =

dB( p)

p = pк

Пример

Дано: изображение:

F ( p) = I ( p) =

p + 10

D( p)

, ( Ac)

Определить:

оригинал.

p3 + 6 p2 + 8 p B( p)

Решение:

B( p) = p3 + 6 p2 + 8 p = p( p2 + 6 p + 8) = 0 .

p1 = 0 , p2 = −2 (1

) , p3 = −4 (1

) ,

B' ( p) = 3 p2 + 12 p + 8 ,

n=3

( pк )

i(t) = ∑

e pкt ,

к=1

( pк )

i(t) =

0 + 10

e0t +

−2 + 10

e(−2)t +

−4 + 10

e(−4)t

3 (−4)2

+ 12 (−4) + 8

3 02 + 12 0 + 8

3 (−2)2 + 12 (−2) + 8

i(t) = 1, 25 − 2e−2t

+ 0,75e−4t

А.

Пример

Дано: изображение:

2 104 p + 2 106

D( p)

Определить:

F ( p) = U ( p) =

, (Вc)

оригинал.

p( p2 + 200 p + 2 104 )

B( p)

Решение:

B( p) = p( p2 + 200 p + 2 104 ) = 0 .

p = 0 , p

= −100 ± j100

)

2,3

B' ( p) = ( p2 + 200 p + 2 104 ) + p(2 p + 200) ,

n=3

D( pк )

u(t) = ∑

e pкt ,

к=1

B' ( pк )

u(t) =

2 104 0 + 2 106

eot +

(02 + 200 0 + 2 104 ) + 0(2 0 + 200)

2 104 p2 + 2 106

e p2t +

( p

+ 200 p

+ 2 104 ) + p (2 p

+ 200)

2 104 p3 + 2 106

e p3t =

( p

+ 200 p

+ 2 104 ) + p (2 p

+ 200)

= 100 + 70,5e− j135°e(−100+ j100)t + +70,5e j135°e(−100− j100)t =

= 100 + 2 70,5e−100t

e j(100t −135°) + e− j (100t −135°)

= 100 + 141e−100t cos(100t − 135°), В.

Пример

Дано: изображение:

Определить:

F ( p) = U ( p) =

2 10

+ 2 10

D( p)

, (Вc)

оригинал.

p( p2 + 200 p + 2 104 ) B( p)

Решение:

B( p) = p( p2 + 200 p + 2 104 ) = 0 ,

p = 0 ,

= −100 ± j100 (1

)

2,3

B' ( p) = ( p3 + 200 p2 + 2 104 p)′ = 3p2 + 400 p + 2 104 , тогда

n=3

D( pк )

u(t) = ∑

e pкt =

к=1

B' ( p )

2 104

0 + 2 106

e0 t

2 104 p + 2 106

2 Re

e p2t =

02 + 400 0 + 2 104

3 p2

2 + 400 p2 + 2 104

<<< < Предыдущая 1 23 / 203 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
19.09.201950.08 Кб2АЯ 0762 Экзамен Актуальная версия.docx
#
11.11.2019223.23 Кб8Б3. Б4. История мировой (античной) рабочая прог...doc
#
11.11.2019183.3 Кб4Б3.Б 1_Введение в спецфилологию.ЕВК.ИВМ.doc
#
11.11.2019143.87 Кб6Б3.Б6. Древнерусская литература.doc
#
15.03.20162.08 Mб45Бандурин TOE 1.pdf
#
15.03.20167.22 Mб37Бандурин TOE_2.pdf
#
15.03.2016789.99 Кб78Бандурин Методичка расчет ПП.pdf
#
15.03.2016454.37 Кб70Бандурин Методичка расчет эм полей.pdf
#
15.03.20166.58 Mб52Бандурин Теоретич основы электротехн Теория электрич цепей электромагн поля С.А.Башарин 2004.djvu
#
15.03.20162.76 Mб737Бандурин ТОЭ-3 лекции.docx
#
01.04.2025180.22 Кб0Банк на рынке ценных бумаг.doc