Файловый архив студентов. Файловый архив студентов.
1271 вуз, 4668 предмет.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Российский химико-технологический университет им. Д.И. Менделеева
Предмет:
Химия
Файл:

Patterson, Bailey - Solid State Physics Introduction to theory

.pdf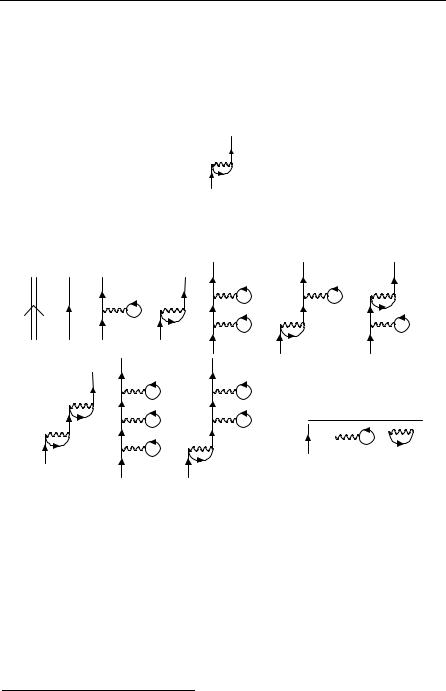
Скачиваний:
1117
Добавлен:
08.01.2014
Размер:
7.07 Mб
Скачать
☆

670 Appendices

which is exactly the same as the Hartree approximation (see (3.21)) since

 

∑l Vklkl = ∫ d3r2φk (r2 )φk (r2 )∑l ∫φl (r1)φl (r1)V (1,2)d3r1 .

(H.8)

It is actually very simple to go from here to the Hartree–Fock approximation – all we have to do is to include the exchange terms in the interactions. These are the “open-oyster” diagrams

where a particle not only strikes a particle in l and creates an instantaneous hole, but is exchanged with it. Doing the partial sum of forward scattering and exchange scattering one has (Mattuck [A.14 p. 91]11):

≈

+

+

+

+

+

+

+

+

+ … =

1

 

 

 

 

 

 

–1– (

+

)

Associating propagators with the terms in the diagram gives

 

 

G+ (k,ω) =

1

.

(H.9)

ω −εk − ∑l(occ.) (Vklkl −Vlkkl ) + iδ

 

 

 

From this we identify the elementary energy excitations as

 

 

εk′ = εk + ∑l(occ.) (Vklkl −Vlkkl ) ,

 

(H.10)

which is just what we got for the Hartree–Fock approximation (see (3.50)).

The random-phase approximation [A.14] can also be obtained by a partial summation of diagrams, and it is equivalent to the Lindhard theory of screening.

11Reproduced with permission from Mattuck RD, A Guide to Feynman Diagrams in the Many-Body Problem, 2nd edn, (4.76) p. 91, Dover Publications, Inc., 1992.

The Many-Body Problem 671

H.6 The Dyson Equation

This is the starting point for many approximations both diagrammatic, and algebraic. Dyson’s equation can be regarded as a generalization of the partial sum technique used in the Hartree and Hartree–Fock approximations. It is exact. To state Dyson’s equation we need a couple of definitions. The self-energy part of a diagram is a diagram that has no incoming or outgoing parts and can be inserted into a particle line. The bubbles of the Hartree method are an example. An irreducible or proper self-energy part is a part that cannot be further reduced into unconnected self-energy parts. It is common to define

Σ

as the sum over all proper self-energy parts. Then one can sum over all repetitions of sigma (∑k,ω) to get

1

=

–1

– Σ

Dyson’s equation yields an exact expression for the propagator,

G(k,ω) =

1

,

(H.11)

ω −εk − ∑l(occ.) (k,ω) + iδk

since all diagrams are either proper diagrams or their repetition. In the Hartree approximation

Σ≈

and in the Hartree–Fock approximation

Σ≈ +

Although the Dyson equation is in principle exact, one still has to evaluate sigma, and this is in general not possible except in some approximation.

We cannot go into more detail here. We have given accurate results for the high and low-density electron gas in Chap. 2. In general, the ideas of Feynman diagrams and the many-body problem merit a book of their own. We have found the book by Mattuck [A.14] to be particularly useful, but note the list of references at the end of this section. We have used some ideas about diagrams when we discussed superconductivity.

Bibliography

Chapter 1

1.1.Anderson PW, Science 177, 393-396 (1972).

1.2.Bacon GE, Neutron Diffraction, Clarendon Press, Oxford, 2nd edn (1962).

1.3.Bradley CJ and Cracknell AP, The Mathematical Theory of Symmetry in Solids: Representation Theory for Point Groups and Space Groups, Clarendon Press, Oxford (1972).

1.4.Brown PJ and Forsyth JB, The Crystal Structure of Solids, Edward Arnold, London, 1975 (Chap. 3).

1.5.Buerger MJ, Elementary Crystallography, John Wiley and Sons, New York, 1956.

1.6.Daw MS, “Model of metallic cohesion: The embedded-atom method,” Phys Rev B 39, 7441-7452 (1989)

1.7.de Gennes PG and Prost J, The Physics of Liquid Crystals, Clarendon Press, Oxford, 2nd edn (1993).

1.8.Evjan HM, Physical Review, 39, 675 (1932)

1.9.Ghatak AK and Kothari LS, An Introduction to Lattice Dynamics, Addison Wesley Publishing Co., Reading, Mass. 1972 p165ff.

1.10.Herzfield CM and Meijer PHE, “Group Theory and Crystal Field Theory,” Solid State Physics, Advances in Research and Applications 12, 1-91 (1961).

1.11.Horton GK, “Ideal Rare-Gas Crystals,” American Journal of Physics, 36(2), 93 (1968).

1.12.Janot C, Quasicrystals, A Primer, Clarendon Press, Oxford (1992).

1.13.Kittel C, Introduction to Solid State Physics, John Wiley and Sons, New York, Seventh Edition, 1996, Chaps. 1-3, 19.

1.14.Koster GF, “Space Groups and Their Representations,” Solid State Physics, Advances in Research and Applications 5, 174-256 (1957).

1.15.Levine D and Steinhardt PJ, Phys Rev Lett 53, 2477-83 (1984).

1.16.Maradudin AA, Montrol EW, and Weiss GW, Theory of Lattice Dynamics in the Harmonic Approximation, Academic Press, N.Y. 1963 p 245.

1.17.Moffatt WG , Pearsall GW, and Wulff J, The Structure and Properties of Materials, Vol. 1, John Wiley and Sons, Inc., New York, 1964.

1.18.Pauling L, Nature of the Chemical Bond, 2nd edn., Cornell University Press, Ithaca, 1945.

1.19.Phillips FC, An Introduction to Crystallography, John Wiley and Sons, Inc., New York, 4th edn., 1971.

1.20.Pollock Daniel D, “Physical Properties of Materials for Engineers,” CRC Press, Boca Raton, 1993.

1.21.Shechtman D, Blech I, Gratias D, and Cahn JW, Phys Rev Lett 53, 1951-3 (1984).

674 Bibliography

1.22.Steinhardt PJ and Ostlund S, The Physics of Quasicrystals, World Scientific Publishing, Singapore, 1987.

1.23.Streetman BG, Solid State Electronic Devices, Prentice Hall, Englewood Cliffs, NJ, 4th edn. (1995).

1.24.Tinkham M, Group Theory and Quantum Mechanics, McGraw-Hill Book Company, New York, 1964.

1.25.Tosi MP, “Cohesion of Ionic Solids in the Born Model,” Solid State Physics, Advances in Research and Applications 16, 1-120 (1964).

1.26.Tran HT and Perdew JP, “How Metals Bind: The deformable jellium model with correlated electrons,” Am J Phys 71, 1048-1061 (2003).

1.27.Webb MB and Lagally MG, “Elastic Scattering of Low Energy Electrons from Surfaces,” Solid State Physics, Advances in Research and Applications 28, 301-405 (1973).

1.28.West Anthony R, Solid State Chemistry and its Properties, John Wiley and Sons, New York, 1984.

1.29.Wigner EP and Seitz F, “Qualitative Analysis of the Cohesion in Metals,” Solid State Physics, Advances in Research and Applications 1, 97-126 (1955).

1.30.Wyckoff RWG, “Crystal Structures,” Vols 1-5, John Wiley and Sons, New York 1963-1968.

Chapter 2

2.1.Anderson PW, Science 177, 393-396 (1972).

2.2.Bak TA (ed), Phonons and Phonon Interactions, W A Benjamin, New York, 1964.

2.3.Bilz H and Kress W, Phonon Dispersion Relations in Insulators, Springer, 1979

2.4.Blackman M, “The Specific Heat of Solids,” Encyclopedia of Physics, Vol. VII, Part 1, Crystal Physics 1, Springer Verlag, Berlin, 1955, p. 325.

2.5.Born M and Huang K, Dynamical Theory of Crystal Lattices, Oxford University Press, New York, 1954.

2.6.Brockhouse BN and Stewart AT, Rev. Mod Phys 30, 236 (1958).

2.7.Brown FC, The Physics of Solids, W A Benjamin, Inc., New York, 1967, Chap. 5.

2.8.Choquard P, The Anharmonic Crystal, W A Benjamin, Inc., New York (1967).

2.9.Cochran W, “Interpretation of Phonon Dispersion Curves,” in Proceedings of the International Conference on Lattice Dynamics, Copenhagen, 1963, Pergamon Press, New York, 1965.

2.10.Cochran W, “Lattice Vibrations,” Reports on Progress in Physics, Vol. XXVI, The Institute of Physics and the Physical Society, London, 1963, p. 1. See also Cochran W, The Dynamics of Atoms in Crystals, Edward Arnold, London, 1973.

2.11.deLauney J, “The Theory of Specific Heats and Lattice Vibrations,” Solid State Physics: Advances in Research and Applications 2, 220-303 (1956).

2.12.Dick BG Jr, and Overhauser AW, Physical Review 112, 90 (1958).

2.13.Dorner B, Burkel E, Illini T, and Peisl J, Z für Physik 69, 179-183 (1989)

2.14.Dove MT, Structure and Dynamics, Oxford University Press, 2003.

2.15.Elliott RJ and Dawber DG, Proc. Roy. Soc. A223, 222 (1963)

2.16.Ghatak K and Kothari LS, An Introduction to Lattice Dynamics, Addison-Wesley Publ. Co., Reading, MA, 1972, Chap. 4.

Chapter 2

675

 

 

2.17.Grosso G and Paravicini GP, Solid State Physics, Academic Press, New York, 2000, Chaps. VIII and IX.

2.18.Huntington HB, “The Elastic Constants of Crystals,” Solid State Physics: Advances in Research and Applications 7, 214-351 (1958).

2.19.Jensen HH, “Introductory Lectures on the Free Phonon Field,” in Phonons and Phonon Interactions, Bak TA (ed), W. A. Benjamin, New York, 1964.

2.20.Jones W and March NA, Theoretical Solid State Physics, John Wiley and Sons, (1973), Vol I, Chap. 3.

2.21.Joshi SK and Rajagopal AK, “Lattice Dynamics of Metals,” Solid State Physics: Advances in Research and Applications 22, 159-312 (1968).

2.22.Kunc K, Balkanski M, and Nusimovici MA, Phys Stat Sol B 71, 341; 72, 229, 249 (1975).

2.23.Lehman GW, Wolfram T, and DeWames RE, Physical Review, 128(4), 1593 (1962).

2.24.Leibfried G and Ludwig W, “Theory of Anharmonic Effects in Crystals,” Solid State Physics: Advances in Research and Applications 12, 276-444 (1961).

2.25.Lifshitz M and Kosevich AM, “The Dynamics of a Crystal Lattice with Defects,” Reports on Progress in Physics, Vol. XXIX, Part 1, The Institute of Physics and the Physical Society, London, 1966, p. 217.

2.26.Maradudin A, Montroll EW, and Weiss GH, “Theory of Lattice Dynamics in the Harmonic Approximation,” Solid State Physics: Advances in Research and Applications, Supplement 3 (1963).

2.27.Messiah A, Quantum Mechanics, North Holland Publishing Company, Amsterdam, 1961, Vol. 1, p 69.

2.28.Montroll EW, J. Chem. Phys. 10, 218 (1942), 11, 481 (1943).

2.29.Schaefer G, Journal of Physics and Chemistry of Solids 12, 233 (1960).

2.30.Scottish Universities Summer School, Phonon in Perfect Lattices and in Lattices with Point Imperfections, 1965, Plenum Press, New York, 1960.

2.31.Shull CG and Wollan EO, “Application of Neutron Diffraction to Solid State Problems,” Solid State Physics, Advances in Research and Applications 2, 137 (1956).

2.32.Srivastava GP, The Physics of Phonons, Adam Hilger, Bristol, 1990.

2.33.Strauch D, Pavone P, Meyer AP, Karch K, Sterner H, Schmid A, Pleti Th, Bauer R, Schmitt M, “Festorkorperproblem,” Advances in Solid State Physics 37, 99-124 (1998), Helbig R (ed), Braunschweig/Weisbaden: Vieweg.

2.34.Toya T, “Lattice Dynamics of Lead,” in Proceedings of the International Conference on Lattice Dynamics, Copenhagen, 1963, Pergamon Press, New York, 1965.

2.35.Van Hove L, Phys Rev 89, 1189 (1953).

2.36.Vogelgesang R et al, Phys Rev B54, 3989 (1996).

2.37.Wallis RF (ed), Proceedings of the International Conference on Lattice Dynamics, Copenhagen, 1963, Pergamon Press, New York, 1965.

2.38.Ziman JM, Electrons and Phonons, Oxford, Clarendon Press (1962).

2.39.1962 Brandeis University Summer Institute Lectures in Theoretical Physics, Vol. 2, W. A. Benjamin, New York, 1963.

676 Bibliography

Chapter 3

3.1.Altman SL, Band Theory of Solids, Clarendon Press, Oxford, 1994. See also Singleton J, Band Theory and Electronic Structure, Oxford University Press, 2001.

3.2.Aryasetiawan F and Gunnarson D, Rep Prog Phys 61, 237 (1998).

3.3.Austin BJ et al, Phys Rev 127, 276 (1962)

3.4.Berman R, Thermal Conduction in Solid, Clarendon Press, Oxford, 1976, p. 125.

3.5.Blount EI, “Formalisms of Band Theory,” Solid State Physics, Advances in Research and Applications, 13, 305-373 (1962).

3.6.Blount EI, Lectures in Theoretical Physics, Vol. V, Interscience Publishers, New York, 1963, p422ff.

3.7.Bouckaert LP, Smoluchowski R, and Wigner E, Physical Review, 50, 58 (1936).

3.8.Callaway J and March NH, “Density Functional Methods: Theory and Applications,” Solid State Physics, Advances in Research and Applications, 38, 135-221 (1984).

3.9.Ceperley DM and Alder BJ, Phys Rev Lett 45, 566 (1980).

3.10.Chelikowsky JR and Louie SG (eds), Quantum Theory of Real Materials, Kluwer Academic Publishers, Dordrecht, 1996.

3.11.Cohen ML, Physics Today 33, 40-44 (1979)

3.12.Cohen ML and Chelikowsky JR, Electronic Structure and Optical Properties of Semiconductors, Springer-Verlag, Berlin, 2nd edn. (1989).

3.13.Cohen ML and Heine V, “The Fitting of Pseudopotentials to Experimental Data and their Subsequent Application,” Solid State Physics, Advances in Research and Applications, 24, 37-248 (1970).

3.14.Cohen M and Heine V, Phys Rev 122, 1821 (1961).

3.15.Cusack NE, The Physics of Disordered Matter, Adam Hilger, Bristol, 1987, see especially Chaps. 7 and 9.

3.16.Dimmock JO, “The Calculation of Electronic Energy Bands by the Augmented Plane Wave Method,” Solid State Physics, Advances in Research and Applications,

26, 103-274 (1971).

3.17.Fermi E, Nuovo Cimento 2, 157 (1934)

3.18.Friedman B, Principles and Techniques of Applied Mathematics, John Wiley and Sons, New York, 1956.

3.19.Harrison WA, Pseudopotentials in the theory of Metals, W A Benjamin, Inc., New York, 1966.

3.20.Heine V, “The Pseudopotential Concept,” Solid State Physics, Advances in Research and Applications, 24, 1-36 (1970).

3.21.Herring C, Phys Rev 57, 1169 (1940).

3.22.Herring C, Phys Rev 58, 132 (1940).

3.23.Hohenberg PC and Kohn W, “Inhomogeneous Electron Gas,” Phys Rev, 136, B804-871 (1964).

3.24.lzynmov YA, Advances in Physics 14(56), 569 (1965).

3.25.Jones RO and Gunnaisson O, “The Density Functional Formalism, its Applications and Prospects,” Rev Modern Phys, 61, 689-746 (1989).

3.26.Jones W and March NH, Theoretical Solid State Physics, Vol. 1 and 2, John Wiley and Sons, 1973.

3.27.Kohn W, “Electronic Structure of Matter–Wave Functions and Density Functionals,” Rev Modern Phys, 71, 1253-1266 (1999).

Chapter 3

677

 

 

3.28.Kohn W and Sham LJ, “Self Consistent Equations Including Exchange and Correlation Effects,” Phys Rev, 140, A1133-1138 (1965).

3.29.Kohn W and Sham LJ, Phys Rev 145, 561 (1966).

3.30.Kronig and Penny, Proceedings of the Royal Society (London), A130, 499 (1931).

3.31.Landau L, Soviet Physics JETP, 3, 920 (1956).

3.32.Loucks TL, Phys Rev Lett, 14, 693 (1965).

3.33.Löwdin PO, Advances in Physics 5, 1 (1956)

3.34.Marder MP, Condensed Matter Physics, John Wiley and Sons, Inc., New York, 2000.

3.35.Mattuck RD, A Guide to Feynman Diagrams in the Many-Body Problem, McGrawHill Book Company, New York, 2nd Ed., 1976. See particularly Chap. 4.

3.36.Negele JW and Orland H, Quantum Many Particle Systems, Addison-Wesley Publishing Company, Redwood City, California (1988).

3.37.Nemoshkalenko VV and Antonov VN, Computational Methods in Solid State Physics, Gordon and Breach Science Publishers, The Netherlands, 1998.

3.38.Parr RG and Yang W, Oxford Univ. Press, New York, 1989.

3.39.Pewdew JP and Zunger A, Phys Rev B23, 5048 (1981).

3.40.Phillips JC and Kleinman L, Phys Rev 116, 287-294 (1959).

3.41.Pines D, The Many-Body Problem, W A Benjamin, New York, 1961.

3.42.Raimes S, The Wave Mechanics of Electrons in Metals, North-Holland Publishing Company, Amsterdam (1961).

3.43.Reitz JR, “Methods of the One-Electron Theory of Solids,” Solid State Physics, Advances in Research and Applications, 1, 1-95 (1955).

3.44.Schlüter M and Sham LJ, “Density Functional Techniques,” Physics Today, Feb. 1982, pp. 36-43.

3.45.Singh DJ, Plane Waves, Pseudopotentials, and the APW Method, Kluwer Academic Publishers, Boston (1994).

3.46.Singleton J, Band Theory and Electronic Properties of Solids, Oxford University Press (2001).

3.47.Slater JC [88, 89, 90].

3.48.Slater JC, “The Current State of Solid-State and Molecular Theory,” International Journal of Quantum Chemistry, I, 37-102 (1967).

3.49.Slater JC and Koster GF, Phys Rev 95, 1167 (1954).

3.50.Slater JC and Koster GF, Phys Rev 96, 1208 (1954).

3.51.Smith N, “Science with soft x-rays,” Physics Today 54(1), 29-54 (2001).

3.52.Spicer WE, Phys Rev 112, p114ff (1958).

3.53.Stern EA, “Rigid-Band Model of Alloys,” Phys Rev, 157(3), 544 (1967).

3.54.Thouless DJ, The Quantum Mechanics of Many-Body Systems, Academic Press, New York, 1961.

3.55.Tran HT and Pewdew JP, “How metals bind: The deformable-jellium model with correlated electrons,” Am. J. Phys. 71(10), 1048-1061 (2003).

3.56.Wannier GH, “The Structure of Electronic Excitation Levels in Insulating Crystals,” Phys Rev 52, 191-197, (1937).

3.57.Wigner EP and Seitz F, “Qualitative Analysis of the Cohesion in Metals,” Solid State Physics, Advances in Research and Applications, 1, 97-126 (1955).

3.58.Woodruff TO, “The Orthogonalized Plane-Wave Method,” Solid State Physics, Advances in Research and Applications, 4, 367-411 (1957).

3.59.Ziman JM, “The Calculation of Bloch Functions,” Solid State Physics, Advances in Research and Applications, 26, 1-101 (1971).

678 Bibliography

Chapter 4

4.1.Anderson HL (ed), A Physicists Desk Reference, 2nd edn, Article 20: Frederikse HPR, p. 310, AIP Press, New York, 1989.

4.2.Appel J, “Polarons,” Solid State Physics, Advances in Research and Applications,

21, 193-391 (1968). A comprehensive treatment.

4.3.Arajs S, American Journal of Physics, 37 (7), 752 (1969).

4.4.Bergmann DJ, Physics Reports 43, 377 (1978).

4.5.Brockhouse BN, Rev Modern Physics 67, 735-751 (1995).

4.6.Callaway J, “Model for Lattice Thermal Conductivity at Low Temperatures,”

Physical Review, 113, 1046 (1959).

4.7.Feynman RP, Statistical Mechanics, Addison-Wesley Publ. Co., Reading MA, 1972, Chap. 8.

4.8.Fisher ME and Langer JS, “Resistive Anomalies at Magnetic Critical Points,”

Physical Review Letters, 20(13), 665 (1968).

4.9.Garnett M, Philos. Trans. R. Soc. (London), 203, 385 (1904).

4.10.Geiger Jr. FE and Cunningham FG, “Ambipolar Diffusion in Semiconductors,”

American Journal of Physics, 32, 336 (1964).

4.11.Halperin BI and Hohenberg PC, “Scaling Laws for Dynamical Critical Phenomena,” Physical Review, 177(2), 952 (1969).

4.12.Holland MG, “Phonon Scattering in Semiconductors from Thermal Conductivity Studies,” Physical Review, 134, A471 (1964).

4.13.Howarth DJ and Sondheimer EH, Proc. Roy. Soc. A219, 53 (1953)

4.14.Jan JP, “Galvanomagnetic and Thermomagnetic Effects in Metals,” Solid State Physics, Advances in Research and Applications, 5, 1-96 (1957).

4.15.Kadanoff LP, “Transport Coefficients Near Critical Points,” Comments on Solid State Physics, 1(1), 5 (1968).

4.16.Katsnelson AA, Stepanyuk VS, Szász AI, and Farberovich DV, Computational Methods in Condensed Matter: Electronic Structure, American Institute of Physics, 1992.

4.17.Kawasaki K, “On the Behavior of Thermal Conductivity Near the Magnetic Transition Point,” Progress in Theoretical Physics (Kyoto), 29(6), 801 (1963).

4.18.Klemens PG, “Thermal Conductivity and Lattice Vibration Modes,” Solid State Physics, Advances in Research and Applications, 7, 1-98 (1958).

4.19.Kohn W, Physical Review, 126, 1693 (1962).

4.20.Kohn W, “Nobel Lecture: Electronic Structure of Matter–Wave Functions and density Functionals,” Rev. Modern Phys. 71, 1253-1266 (1998)

4.21.Kondo J, “Resistance Minimum in Dilute Magnetic Alloys,” Progress in Theoretical Physics (Kyoto), 32, 37 (1964).

4.22.Kothari LS and Singwi KS, “Interaction of Thermal Neutrons with Solids,” Solid State Physics, Advances in Research and Applications, 8, 109-190 (1959).

4.23.Kuper CG and Whitfield GD, POLARONS AND EXCITONS, Plenum Press, New York, 1962. There are lucid articles by Fröhlich, Pines, and others here, as well as a chapter by F. C. Brown on experimental aspects of the polaron.

4.24.Langer JS and Vosko SH, Journal of Physics and Chemistry of Solids, 12, 196 (1960).

Chapter 5

679

 

 

4.25.MacDonald DKC, “Electrical Conductivity of Metals and Alloys at Low Temperatures,” Encyclopedia of Physics, Vol. XIV, Low Temperature Physics I, Springer-Verlag, Berlin, 1956, p. 137.

4.26.Madelung O, Introduction to Solid State Theory, Springer-Verlag, 1978, pp. 153155, 183-187, 370-373. A relatively simple and clear exposition of both the large and small polaron.

4.27.Mahan GD, Many Particle Physics, Plenum Press, New York, 1981, Chaps. 1 and 6. Green’s functions and diagrams will be found here.

4.28.Mattuck RD, A Guide to Feynman Diagrams in the Many-Body Problem, McGrawHill Book Company, New York, 1967.

4.29.McMillan WL and Rowell JM, Physical Review Letters, 14 (4), 108 (1965).

4.30.Mendelssohn K and Rosenberg HM, “The Thermal Conductivity of Metals a Low Temperatures,” Solid State Physics, Advances in Research and Applications, 12, 223-274 (1961).

4.31.Mott NF, Metal-Insulator Transitions, Taylor and Francis, London, 1990 (2nd edn).

4.32.Olsen JL, Electron Transport in Metals, Interscience, New York, 1962.

4.33.Patterson JD, “Modern Study of Solids,” Am. J. Phys. 32, 269-278 (1964).

4.34.Patterson JD, “Error Analysis and Equations for the Thermal Conductivity of Composites,” Thermal Conductivity 18, Ashworth T and Smith DR (eds), Plenum Press, New York, 1985, pp 733-742.

4.35.Pines D, “Electron Interactions in Metals,” Solid State Physics, Advances in Research and Applications, 1, 373-450 (1955).

4.36.Reynolds JA and Hough JM, Proc. Roy. Soc. (London), B70, 769-775 (1957).

4.37.Sham LJ and Ziman JM, “The Electron-Phonon Interaction,” Solid State Physics, Advances in Research and Applications, 15, 223-298 (1963).

4.38.Stratton JA, Electromagnetic Theory, McGraw Hill, 1941, p. 211ff.

4.39.Ziman JM, Electrons and Phonons, Oxford, London, 1962, Chap. 5 and later chapters (esp. p. 497)

Chapter 5

5.1.Alexander, W. and Street A, Metals in the Service of Man, 7th edn. Middlesex, England: Penguin, 1979.

5.2.Blatt FJ, Physics of Electronic Conduction in Solids, McGraw-Hill (1968).

5.3.Borg RJ and Dienes GJ, An Introduction to Solid State Diffusion, Academic Press, San Diego, 1988, p 148-151.

5.4.Cottrell A, Introduction to the Modern Theory of Metals, the Institute of Metals, London, 1988.

5.5.Cracknell AP and Wong KC, The Fermi Surface: Its Concept, Determination, and Use in the Physics of Metals, Clarendon Press, Oxford, 1973.

5.6.Duke CB, “Tunneling in Solids,” in Supplement 10, Solid State Physics, Advances in Research and Applications (1969).

5.7.Fiks VB, Sov Phys Solid State, 1, 14 (1959).

5.8.Fisk Z et al, “The Physics and Chemistry of Heavy Fermions,” Proc Natl Acad Sci USA 92, 6663-6667 (1995).

680 Bibliography

5.9.Gantmakher VF, “Radio Frequency Size Effect in Metals,” Progress in Low Temperature Physics, Vol. V, Gorter CJ (ed), North-Holland Publishing Company, Amsterdam, 1967, p. 181.

5.10.Harrison WA, Applied Quantum Mechanics, World Scientific, Singapore, 2000, Chap. 21.

5.11.Harrison WA and Webb MB (eds), The Fermi Surface, John Wiley and Sons, New York, 1960.

5.12.Huang K, Statistical Mechanics, John Wiley and Sons, 2nd edn, 1987, pp 247-255.

5.13.Huntington HB and Grove AR, J Phys Chem Solids, 20, 76 (1961).

5.14.Kahn AH and Frederikse HPR, “Oscillatory Behavior of Magnetic Susceptibility and Electronic Conductivity,” Solid State Physics, Advances in Research and Applications 9, 259-291 (1959).

5.15.Kittel C and Kroemer H, Thermal Physics, W. H. Freeman and Company, San Francisco, 2nd edn., 1980, Chap. 11.

5.16.Langenberg DN, “Resource Letter OEPM-1 on the Ordinary Electronic Properties of Metals,” American Journal of Physics, 36 (9), 777 (1968).

5.17.Lax B and Mavroides JG, “Cyclotron Resonance,” Solid State Physics, Advances in Research and Applications 11, 261-400 (1960).

5.18.Lloyd JR, “Electromigration in integrated circuit conductors”, J Phys D: Appl Phys 32, R109-R118 (1999).

5.19.Mackintosh AR, Sci. Am. 209, 110, (1963).

5.20.Onsager L, Phil. Mag. 93, 1006-1008 (1952).

5.21.Overhauser AW, “Charge Density Wave,” Solid State Physics Source Book, Parker SP (ed), McGraw-Hill Book Co., 1987, pp 142-143.

5.22.Overhauser AW, “Spin-Density Wave,” Solid State Physics Source Book, Parker SP (ed), McGraw-Hill Book Co., 1987, pp. 143-145

5.23.Peierls R, More Surprises in Theoretical Physics, Princeton University Press, NJ, 1991, p29.

5.24.Pippard AB, “The Dynamics of Conduction Electrons,” Low Temperature Physics, deWitt C, Dreyfus B, and deGennes PG (eds), Gordon and Breach, New York, 1962. Also Pippard AB, Magnetoresistance in Metals, Cambridge University Press, 1988.

5.25.Radousky HB, Magnetism in Heavy Fermion Systems, World Scientific, Singapore, 2000.

5.26.Shapiro SL and Teukolsky SA, Black Holes, White Dwarfs and Neutron Stars: The Physics of Compact Objects, John Wiley and Sons, Inc., New York, 1983.

5.27.Shoenberg D, Magnetic Oscillations in Metals, Cambridge University Press, 1984.

5.28.Sorbello RS, “Theory of Electromigration,” Solid State Physics, Advances in Research and Applications 51, 159-231 (1997).

5.29.Stark RW and Falicov LM, “Magnetic Breakdown in Metals,” Progress in Low Temperature Physics, Vol. V, Gorter CJ (ed), North-Holland Publishing Company, Amsterdam, 1967, p. 235.

5.30.Stewart GR, “Heavy-Fermion Systems,” Rev Modern Physics, 56, 755-787 (1984).

5.31.Thorne RE, “Charge Density Wave Conductors,” Physics Today, pp 42-47 (May 1996).

5.32.Wigner E and Huntington HB, J Chem Phys 3, 764-770 (1935).

5.33.Wilson AH, The Theory of Metals, Cambridge, 1954.

Соседние файлы в предмете Химия
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности